Estimation quality for ordinal insolvency prognoses
Estimates of the quality of ordinal insolvency prognoses measure the quality of ordinal insolvency prognoses . Ordinal insolvency prognoses are prognoses about the relative default probabilities of the rated companies like "company Y is more likely to fail than company X but less likely than company Z".
Ordinal insolvency forecasts could theoretically be differentiated as desired, but ordinal rating systems have prevailed in practice, which communicate their results on a discrete, 7- or 17-point scale in a notation adopted by Standard & Poor’s (S&P).
Importance of ordinal appraisal measures
Even if ordinal insolvency prognoses are more general than categorical insolvency prognoses , only comparative statements about the relative default risk of companies are insufficient for most applications. Rather, quantitative default forecasts are also required, for example to be able to specify whether a risk premium of 1.5% p. a. for a bullet , unsecured and senior credit with three years maturity is appropriate for a company whose rating classification stating that it "currently has the capacity to meet its financial obligations. However, adverse business, financial or macroeconomic conditions would likely affect his ability and willingness to meet his financial obligations ”.
Nevertheless, it is worth examining the quality of estimates for ordinal insolvency prognoses:
- In terms of their intention, they correspond to what the rating agencies promise to deliver.
- They are now a dominant method for assessing the quality of rating results.
- There are numerous possibilities of graphical representation for the ordinal estimation quality of rating systems, which also facilitates the communicability of the key figures derived from these representations.
- A high degree of selectivity , as measured by quality measures for ordinal insolvency prognoses, is also important for the quality of cardinal insolvency prognoses - more important than correct calibration . It is easier to generate "correct" (calibrated) than selective failure probabilities.
- In the empirical comparison of different rating procedures on the basis of identical samples, the order of the quality of the individual procedures according to ordinal estimated quality measures often also corresponds to the order of quality based on cardinal estimated quality measures. Differences in quality of different methods seem to be less in a different ability to issue calibrated failure prognoses, which is only relevant for cardinal quality measures, but rather in a different ability to deliver selective prognoses, which is relevant for both ordinal and cardinal estimated quality measures.
- For those aspects of cardinal insolvency prognoses that cannot already be measured with the instruments developed for assessing ordinal insolvency prognoses, especially for the aspect of calibrating insolvency prognoses, no meaningful test procedures are currently available - if the default probabilities of the various companies are not are uncorrelated . However, the actual relevance of this theoretical objection is still controversial. There are empirical indications that the corresponding segment-specific correlation parameters assumed within the framework of Basel II are set too high by a factor of 15 to 120 (on average around 50).
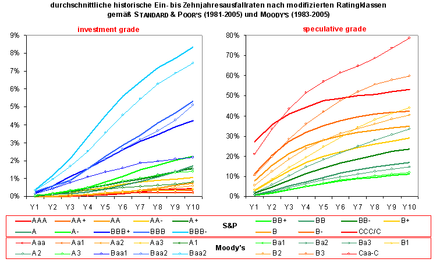
Even if the rating agencies do not want to issue cardinal default forecasts for any specified period ex ante with the ordinal rating grades they have assigned, they demonstrate the quality of their rating assessments and the like. a. with their ability to identify companies with significantly different, monotonously increasing failure frequencies (see the two following figures for the average rating class-specific one- and multi-year failure rates according to S&P and Moody's).
The two figures show that the rating agencies were able, with their ex-ante rating grades , to separate ex-post groups of companies with very different realized default rates.
This is a necessary prerequisite in order to be able to make selective failure forecasts, but not a sufficient one. For example, the following extreme cases would be compatible with the representations in the figures above:
- Extreme case I: The rating system assigns almost all companies to a medium rating level (see the first figure), for example BB or Ba2, and only very few companies to other rating levels.
- Extreme case II: The rating assigns almost all companies to the extreme rating levels, i. H. either AAA or CCC / C, one and only a few in the middle rating levels.
In case I, the rating would be almost worthless, as it practically did not allow any differentiation between the various debtors. In case II, on the other hand, the information benefit would be considerable: the rating would always make "extreme forecasts" - that is, predict either an extremely low or an extremely high probability of default - and the forecasts would mostly be correct - an AAA rating would almost never and within a year CCC / C rating would be followed by default in at least 25% –30% of all cases.
In order to determine the ordinal quality of a rating system, it is therefore not only necessary to know the rating class-specific default rates, but also the distribution of the companies in the individual rating classes.
Graphical appraisal
The ability of a rating system to separate “good” and “bad” debtors with great reliability can be visualized using ROC or CAP curves (cumulative accuracy profile) and quantified using various key figures that can be converted into one another. Further names for ROC or CAP curves are reconnaissance profile, power curve, Lorenz curve, Gini curve, lift curve, dubbed curve or ordinal dominance graph.
The ROC curve of a procedure results from the set of all combinations of hit rates (100% - error I type ) and " false alarm rates " ( error II. Type ), which an insolvency forecast procedure based on different cut-off scores, ie . H. when converting cardinal or ordinal insolvency forecasts into categorical insolvency forecasts . If the cut-off value was “too sharp”, all companies would be predicted to be insolvent (100% hit rate (= 0% error I type); 100% false alarm rate (= 100% error II type)). Cutoff value, none of the companies would be forecast to be likely to be insolvent (0% hit rate; 0% false alarm rate). Even between these extreme cases there is a balance between hit and false alarm rates. The quality of ordinal insolvency prognoses is reflected in the nature of this compensation. A perfect forecasting procedure would not have to “wrongly” exclude a single debtor in order to record 100% of all defaults (vertical course of the ROC curve from (0%; 0%) to (0%; 100%)), a subsequent tightening of the cut-off value would only lead to an increase in the false alarm rate (horizontal course of the ROC curve from (0%; 100%) to (100%; 100%)). The ROC curve of a rating procedure, on the other hand, whose evaluations were purely random, would run along the main diagonal - every percentage point in the improvement of the hit rate would have to be paid for with one percentage point in the deterioration of the false alarm rate.
Real bankruptcy forecasting ROC curves are concave in shape. The concavity of an ROC curve implies that the realized default rates decrease with better creditworthiness, i.e. This means that the underlying rating system is "semi-calibrated".
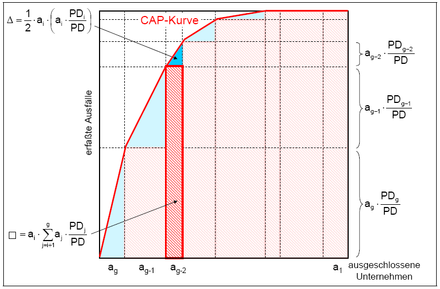
CAP curves result from the application of a construction principle that is only slightly modified compared to ROC curves. The X-axis does not show the "false alarm rates" (type II errors), but the proportion of companies that have to be excluded from the forecasting process - regardless of whether they are actual failures or non-failures to achieve a certain "hit rate" (100% error of the first type). The CAP curve of a perfect rating runs steeply to the top right, starting from the point (0%; 0%) - but not vertically, as at least PD% of all companies must be excluded in order to record all failures (see the graphic above, right) .
If the ROC / CAP curve of a method A1 is regularly to the left above the ROC / CAP curve of another method A2 when assessing the same companies, method A1 delivers better forecasts than method A2 for every conceivable cut-off value (see the graphic above) . If the relative advantage of a method only depends on its relative estimation quality, then method A1 would always be preferable to method A2 - regardless of the individual specifics of the decision-maker, for example with regard to its costs for errors I and II. Art. However, the ROC curves of two intersect Methods B1 and B2 (see the figure above, right), neither of the two methods is objectively superior to the other. In the example chosen, method B1 is better able than B2 to differentiate within the “good companies”, while method B2 has a higher degree of selectivity in the area of “bad companies”. If the decision maker is not forced to use either only one or only the other method, he can possibly combine methods B1 and B2 to form a third method B3 in such a way that this is superior to both B1 and B2. The same applies to methods A1 and A2: although A2 is strictly dominated by A1, a combination of A1 and A2 can possibly generate a method A3 that is superior not only to A2 but also to A1. In empirical studies, for example, the forecast quality of bank ratings based exclusively on key figures could be improved by including “soft factors” , although the quality of the forecast of the key figure-based ratings was better than the quality of the forecast of the soft factor ratings.
In addition to graphical representations, key figures are also required for practical use in measuring the estimation quality of insolvency forecasts in order to present the information contained in CAP or ROC curves as compactly as possible. The minimum requirement for such an index is that this index must be defined for all ROC curves and that, if the ROC curve of a method A1 is on the left above the ROC curve A2, the quality measure associated with A1 must have a higher value as the A2 associated quality measure.
Quantitative appraisal
The quality measure usually used in connection with ROC curves is the content of the area under the ROC curve:
Formula 1:
The area under the ROC curve corresponds to the probability that for two randomly selected individuals, one drawn from the defaulting companies and one from the non-defaulting companies, the non-defaulting company has a better score than the defaulting company. With a perfect rating system, AUC is always 100%; with a purely random score (naive rating system), the expected value for AUC is 50%. To adjust the value range of the quality measure to the interval [-100%; +100%] instead of [0%; 100%] and to show "naive forecasts" with an expected value of 0% instead of 50%, the Accuracy Ratio is determined on the basis of the following:
Formula 2:
The parameter AR can also be represented as a special case of other common ordinal parameters. In contrast to the procedure for ROC curves, it is not usual to show the AUC dimensions calculated on the basis of CAP curves. Only the calculation of the CAP accuracy ratio, which is slightly modified compared to the ROC curve, with:
Formula 3:
Formula 3b:
where A´ stands for the area between the CAP curve and the diagonal and B´ for the area between the diagonal and the CAP curve, which a perfect rating procedure could achieve at most, see the graphic on the right in the figure above. It can be shown that and are identical.
For a rating system with g discrete classes, the integral ∫CAP (x) dx can be broken down into g triangular and rectangular sub-areas with known side lengths (see the following figure). The figure shows the area for a rectangular and a triangular area.
Formula 4:
- Legend
- g ... number of discrete rating classes,
- a j ... share of companies in rating class j,
- PD j ... realized failure frequency in rating class j,
- PD ... average probability of failure
By rearranging and inserting it in formula 3b, the result is:
Formula 5: with
Formula 5b:
where kumPD i stands for the proportion of defaults in rating classes 1..i in relation to the total of all defaults. The quality measures presented are defined equally for continuous scores as for scores with a finite number of possible characteristics (rating classes). The combination of continuous scores into discrete rating classes is associated with only minor loss of information, so that the quality of ordinal insolvency forecasts can be determined solely on the basis of the relative frequencies of the individual rating classes and the information on the realized default rates per rating class. This data is, for example, by the rating agencies S & P and Moody's published, but also for other rating systems, such as the credit rating of Creditreform available.
swell
- ↑ This article is based on Bemmann (2005).
- ↑ 17-step scale: 1 = "AAA", 2 = "AA +", 3 = "AA", 4 = "AA-", 5 = "A +", 6 = "A", 7 = "A-", 8 = "BBB +", 9 = "BBB", 10 = "BBB-", 11 = "BB +", 12 = "BB", 13 = "BB-", 14 = "B +", 15 = "B", 16 = "B-", 17 = "CCC / C", 7-point scale: "AAA", "AA", "A", "BBB", "BB", "B", "C".
- ↑ The Basler Committee (2000c, p. 23f) examines the rating symbols of 30 rating procedures from different international rating agencies . 22 agencies use letter combinations to express their rating assessment (approx. 75%), 6 agencies communicate their ratings in the form of grades (20%), only two agencies give their assessment in the form of default probabilities. Of the 22 “letter ratings”, 14 correspond exactly to the detailed S&P notation (17-step scale), 2 to the shortened S&P notation (7-step scale). In the case of banks, on the other hand, numerical rating class designations predominate (approx. 85%) instead of letter combinations (approx. 15%), see English, Nelson (1998, p. 4).
- ↑ Standard & Poor's has been using the rating class representation, modified by plus and minus signs, since 1974. Moody's, on the other hand, has only been around since 1982, see Cantor, Packer (1994, p. 2)
- ↑ See the definition for rating level B according to S&P (2003b, p. 7, own translation)
- ↑ See also Frerichs, Wahrenburg (2003, p. 13): “Under what circumstances is such a measure area Under the ROC-curve useful? The ranking of borrowers is sufficient for credit risk management if banks are not able to charge different credit risk premiums for different customers in the market. In this case, banks maximize their risk-adjusted returns by not granting credit to customers with negative expected returns which is equivalent to defining a minimum credit score. Yet, this line of thought does not lead us to the AUC as a measure of system quality, but to the concept of minimized expected error costs. The AUC measures the quality of the complete ranking and not only of one threshold. Only if the threshold is difficult to define in practice, the AUC may be a sensible measure. "- or in short and concise:" There are no bad loans, only bad prices. ", See Falkenstein, Boral, Kocagil (2000, p. 5).
- ↑ Cantor, Mann (2003, p. 6): "Moody's primary objective is for its ratings to provide an accurate relative (ie, ordinal) ranking of credit risk at each point in time, without reference to an explicit time horizon." And Cantor, Mann (2003, p. 1): "Moody's does not target specific default rates for the individual rating categories.", But also: "Moody's also tracks investment-grade default rates and the average rating of defaulting issuers prior to their defaults . These metrics measure Moody's success at meeting a secondary cardinal or absolute rating system objective, namely that ratings are useful to investors who employ simple rating 'cutoffs' in their investment eligibility guidelines. ", See ibid.
- ↑ Basel Committee (2000c, p. 2) "Most firms report that they rate risk on a relative - rather than absolute - scale, and most indicate that they rate 'across the business cycle", suggesting that ratings should not be significantly in principle affected by purely cyclical influences. ”Of the 15 rating agencies that provided information on this, 13 stated that they measure the“ relative risk ”of companies with their rating, only 2 agencies measure the“ absolute risk ”of companies according to their own information ( KMV Corporation and Upplysningscentralen AB), see ibid. (P. 23f).
- ↑ See for example McQuown (1993, p. 5ff), Keenan, Sobehart (1999, p. 5ff), Stein (2002, p. 5ff.), Fahrmeir, Henking, Hüls (2002, p. 22f), Engelmann, Hayden, Taschen (2003, p. 3ff.), Deutsche Bundesbank (2003a, p. 71ff.), OeNB (2004a, p. 113ff.). The rating agencies Standard and Poor's (2006, p. 48) and Moody's (2006, p. 11ff.) Also measure the quality of their rating systems using the methods and key figures presented in this section.
- ↑ Blochwitz, Liebig, Nyberg (2000, p. 3): “It is usually much easier to recalibrate a more powerful model than to add statistical power to a calibrated model. For this reason, tests of power are more important in evaluating credit models than tests of calibration. This does not imply that calibration is not important, only that it is easier to carry out. ", Analogous to Stein (2002, p. 9)
- ↑ The calibration of a rating system is described in Sobehart et al. (2000, p. 23f.) Or Stein (2002, p. 8ff.).
- ↑ See, for example, Krämer, Güttler (2003) for comparing the estimated quality of default forecasts by S&P and Moody's or Sobehart, Keenan, Stein (2000, p. 14) for comparing the estimated quality of six different methods using ordinal and cardinal estimation quality indicators.
- ↑ see Basel Committee (2005a, p. 31f.): “These [cardinal] measures appear to be of limited use only for validation purposes as no generally applicable statistical tests for comparisons are available. [...] The [Basle Committee's Validation] Group has found that the Accuracy Ratio (AR) and the ROC measure appear to be more meaningful than the other above-mentioned indices because of their statistical properties. For both summary statistics, it is possible to calculate confidence intervals in a simple way. [...] However, due to the lack of statistical test procedures applicable to the Brier score, the usefulness of this metric for validation purposes is limited. "And ibid., P. 34:" At present no really powerful tests of adequate calibration are currently available. Due to the correlation effects that have to be respected there even seems to be no way to develop such tests. Existing tests are rather conservative [...] or will only detect the most obvious cases of miscalibration [...] "
- ↑ Even with moderate default correlations (at least compared to the benchmark values assumed by the supervisory authority), the realized default rates - even for portfolios of any size - can deviate considerably from the expected default rates, see Huschens, Höse (2003, p. 152f.) Or Blochwitz et al. (2004, p. 10).
- ↑ See Scheule (2003, p. 149). The investigations are based on a dataset from the Deutsche Bundesbank, which covers the period 1987-2000 and contains over 200,000 annual financial statements from over 50,000 (West German) companies, 1,500 of which became insolvent, see ibid. (P. 113ff.). On the basis of of Scheule (2003, p.156) portfolio loss loss distribution determined (a concrete model portfolio with an expected failure rate of 1.34%) is largely symmetrical and differs significantly from the typical left share-right skewed distribution type that can occur with strong default correlations results . The 99.9% quantile of both distributions, which is used to determine the capital requirements according to the Basel II rules , differs in the example chosen by a factor of 5 to 6!
- ↑ S&P (2005, p. 28): "Many practitioners utilize statistics from this default study and CreditPro® to estimate probability of default and probability of rating transition. It is important to note that Standard & Poor's ratings do not imply a specific probability of default; However, Standard & Poor's historical default rates are frequently used to estimate these characteristics. "
- ↑ The failure studies by S&P and Moody's are based on issuer ratings (also issuer ratings, corporate credit ratings, implied senior-most ratings, default ratings, natural ratings, estimated senior ratings), which are intended to represent a measure of the companies' expected probability of default, but without specify an explicit forecast horizon, see S&P (2003b, p. 3ff., 61ff.), Cantor, Mann (2003, p. 6f.), Moody's (2004b, p. 8) and Moody's (2005, p. 39). The ratings of specific liabilities of enterprises, so-called issue ratings (issue rating), consider not only the probability of default and the expected loss severity and can therefore be interpreted as a measure of the expected default costs. Depending on the rank of the assessed liability within the capital structure of the company, the security granted and other influencing factors, the issue rating results from surcharges or discounts (usually 1 to 2 points) from the issue rating. The issuer rating of a company generally corresponds to the issue rating of first-class, unsecured liabilities, see ibid.
- ↑ see Cantor, Mann (2003, p. 14)
- ↑ ROC curves have been used in experimental psychology since the early 1950s, see Swets (1988, p. 1287).
- ↑ see Blochwitz, Liebig, Nyberg (2000, p. 33): power curve, lift-curve, dubbed-curve, receiver-operator curve; Falkenstein, Boral, Kocagil (2000, p. 25): Gini curve, Lorenz curve, ordinal dominance graph; Schwaiger (2002, p. 27): Enlightenment profile
- ↑ See Bemmann (2005, Appendix I) for numerous examples of ROC curves for real insolvency forecasting methods.
- ↑ see Krämer (2003, p. 403)
- ↑ Another criterion for the relative advantageousness of the proceedings could be the costs of the proceedings themselves. While banks often use automated (and tend to have few selective) procedures for the classification of smaller loans, more labor-intensive evaluation processes are also worthwhile for larger loans, see Treacy, Carey (2000, p. 905) and Basler Committee (2000b, p. 18f. )
- ↑ see Blochwitz, Liebig, Nyberg (2000, p. 7f.)
- ↑ According to Krämer (2003, p. 402), when comparing rating systems, the “normal case” consists of intersecting ROC and CAP curves: “In this respect, the concept of failure dominance does not help in many applications. [...] The concept of failure dominance [recommends] above all for sorting out substandard systems. ”Predictions with weaker separation (failure-dominated) can be derived from more distinctive forecasts, see Krämer (2003, p. 397f.).
- ↑ See the study by Lehmann (2003, p. 21) in Section 3.4. See Grunert, Norden, Weber (2005), which however only show aggregated key figures for the different models (key figure rating, soft factor rating, combined rating) and no CAP or ROC curves. In the latter study, the predictability of the soft factor rating was even greater than that of the key figure rating (see ibid., p. 519).
- ↑ The reversal of the minimum requirement (“If A1> A2, then the ROC curve of A1 lies to the left above A2”) does not apply. It is only excluded that the A1 associated CAP / ROC curve lies to the right below the A2 associated CAP / ROC curve. It is also conceivable that the CAP / ROC curves of A1 and A2 intersect if A1> A2. Cantor, Mann (2003, p. 12): "Although the accuracy ratio is a good summary measure, not every increase in the accuracy ratio implies an unambiguous improvement in accuracy."
- ↑ see Deutsche Bundesbank (2003a, p. 71ff.)
- ↑ For further, easily interpretable indicators see Lee (1999).
- ↑ see Lee (1999, p. 455)
- ↑ The lowest possible value, 0%, would be achieved by a rating system whose forecasts are always wrong. By negating the forecasts, this rating could be converted into a perfect rating.
- ↑ See Hamerle, Rauhmeier, Rösch (2003, p. 21f.), Which show that the accuracy ratio is a special case of the more general key figure Somer's D, which is also used for variables to be explained with more than two possible characteristics (failure vs. non-failure) is defined. See Somer (1962, pp. 804f.) For an illustration of the relation of Somer's D to other ordinal measures of quality such as Kendall's Tau or Goodman and Kruskal's Gamma.
- ↑ see Engelmann, Hayden, Tasche (2003, p. 23)
- ↑ see Bemmann (2005, p. 22f.)
- ↑ see Bemmann (2005, Section 2.3.4)
- ↑ see Lawrenz, Schwaiger (2002)
literature
- Basel Committee : see Basel Committee on Banking Supervision
- Basel Committee on Banking Supervision (ed.) (2000b): Range of Practice in Banks' Internal Ratings systems , Discussion Paper , Bank for International Settlements (BIS), http://www.bis.org/publ/bcbs66.pdf (18. October 2006), 01/2000
- Basel Committee on Banking Supervision (Ed.) (2000c): Credit Ratings and Complementary Sources of Credit Quality Information , Working Paper # 3, http://www.bis.org/publ/bcbs_wp3.pdf (October 18, 2006), 2000
- Basel Committee on Banking Supervision (Ed.) (2005a): Studies on the Validation of Internal Rating Systems , Working Paper No. 14, http://www.bis.org/publ/bcbs_wp14.pdf (October 24, 2005), revised version, 05/2005
- Bemmann, M. (2005): Improvement of the comparability of estimation quality results of insolvency prognosis studies , in Dresden Discussion Paper Series in Economics 08/2005, http://ideas.repec.org/p/wpa/wuwpfi/0507007.html (November 8th 2006) and http://papers.ssrn.com/sol3/papers.cfm?abstract_id=738648 (November 27, 2006), 2005
- Blochwitz, S., Liebig, T., Nyberg, M. (2000): Benchmarking Deutsche Bundesbank's Default Risk Model, the KMV® Private Firm Model® and Common Financial Ratios for German Corporations , Workshop on Applied Banking Research, Basel Committee for Banking Supervision , http://www.bis.org/bcbs/events/oslo/liebigblo.pdf (August 16, 2004), 2000
- Blochwitz, S., Hohl, S., Taschen, D., Wehn, CS (2004): Validating Default Probabilities on Short Time Series , http://www.chicagofed.org/publications/capital_and_market_risk_insights/2004/validating_default_probabilities.pdf ( Memento from May 16, 2005 on the Internet Archive ) (November 27, 2006), Working Paper, Federal Reserve Bank of Chicago, 05/2004
- Cantor, R., Mann, C. (2003): Measuring the Performance of Corporate Bond Ratings , Special Comment, Report # 77916, Moody's Investor's Service, 04/2003
- Deutsche Bundesbank (Ed.) (2003a): Validation approaches for internal rating systems , in: Monthly Report September 2003, pp. 61–74, http://www.bundesbank.de/download/volkswirtschaft/mba/2003/200309mba_validierung.pdf (30 October 2006), 09/2003
- Engelmann, B., Hayden, E., Taschen, D. (2003): Measuring the Discriminative Power of Rating Systems , Deutsche Bundesbank, Discussion Paper, Series 2: Banking and Financial supervision, http://www.bundesbank.de/ download / banking supervision / dkp / 200301dkp_b.pdf (October 30, 2006), 01/2003
- English, WB, Nelson, WR (1998): Bank Risk Rating of Business Loan , Board of Governors of the Federal Reserve System FEDS Paper No. 98-51, http://ssrn.com/abstract=148753 (October 18, 2006), 12/1998
- Fahrmeir, L. , Henking, A., Hüls, R. (2002): Methods for comparing different scoring methods using the example of the SCHUFA scoring method , Risknews, 11/2002, pp. 20-29, 2002
- Falkenstein, E., Boral, A., Kocagil, AE (2000): RiskCalc ™ for Private Companies II: More Results and the Australian Model , Moody's Investors Service, Rating Methodology, Report # 62265, https://riskcalc.moodysrms.com /us/research/crm/62265.pdf (January 2, 2016), 12/2000
- Frerichs, H., Wahrenburg, M. ( Memento from June 29, 2010 in the Internet Archive ) (2003): Evaluating internal credit rating systems depending on bank size , Working Paper Series: Finance and Accounting, Johann Wolfgang Goethe-Universität Frankfurt Am Main , No. 115, http://ideas.repec.org/p/fra/franaf/115.html (November 14, 2006), 09/2003
- Grunert, J. ( Memento of July 11, 2007 in the Internet Archive ), Norden, L. , Weber, M. (2005): The role of non-financial factors in internal credit ratings , in Journal of Banking and Finance, Vol. 29, pp. 509-531, 2005
- Hamerle, A. ( Memento from April 18, 2009 in the Internet Archive ), Rauhmeier, R., Rösch, D. ( Memento from May 7, 2005 in the Internet Archive ) (2003): Uses and Misuses of Measures for Credit Rating Accuracy , Version 04/2003, Working Paper, University of Regensburg, http://www.defaultrisk.com/_pdf6j4/Uses_n_Misuses_o_Measures_4_Cr_Rtng_Accrc.pdf (January 2, 2016), 2003
- Huschens, S., Höse, S. (2003): Can internal rating systems be evaluated within the framework of Basel II? - To estimate the probability of default through default rates , in: Zeitschrift für Betriebswirtschaft (ZfB), Vol. 73 (2), pp. 139–168, 2003
- Keenan, SC, Sobehart, JR (1999): Performance Measures for Credit Risk Models , Moody's Investors Service, Research Report # 1-10-10-99, http://www.riskmania.com/pdsdata/PerformanceMeasuresforCreditRiskModels.pdf (6 November 2006), 1999
- Krämer, W. (2003): The assessment and comparison of credit default forecasts , in: Kredit und Kapital , Vol. 36 (3), pp. 395-410, 2003
- Krämer, W., Güttler, A. (2003): Comparing the accuracy of default predictions in the rating industry: The case of Moody's vs. S&P , Technical Report series of the SFB 475 No. 23 (University of Dortmund), http://www.wiwi.uni-frankfurt.de/schwerpunkte/finance/wp/332.pdf ( Memento from November 11, 2005 in the Internet Archive ) (November 6, 2006), 2003
- Lawrenz, J., Schwaiger, WSA (2002): Bank Germany: Updating the Quantitative Impact Study (QIS2) from Basel II , in: Risknews 01/2002, pp. 5–30, 2002
- Lee, W.-C. (1999): Probabilistic Analysis of Global Performances of Diagnostic Tests: Interpreting the Lorenz Curve-Based Summary Measures , in Statistics in Medicine, Vol. 18, pp. 455-471, 1999
- Lehmann, B. (2003): Is It Worth the While? The Relevance of Qualitative Information in Credit Rating , EFMA 2003 Helsinki Meetings, http://ssrn.com/abstract=410186 (October 26, 2006), 04/2003
- McQuown, JA (1993): A Comment on Market vs. Accounting-Based Measures of Default Risk , KMV Working Paper, http://www.moodysanalytics.com/microsites/erm/404-ERM.aspx (October 23, 2006), KMV Corporation, 1993
- Moody's (ed.) (2004b): Moody's Rating Symbols & Definitions , Moody's Investors Service, Report # 79004, 08/2004
- Moody's (Ed.) (2005): Default and Recovery Rates of Corporate Bond Issuers, 1920-2004 , Moody's Investors Service, 01/2005
- Moody's (ed.) (2006): Default and Recovery Rates of Corporate Bond Issuers, 1920-2005 , Moody's Investors Service, 01/2006
- OeNB : see Austrian National Bank
- OeNB (Ed.) (2004a): Rating models and validation , series of guidelines on credit risk, https://www.oenb.at/dam/jcr:16742110-9bf6-4b19-aa73-b729509a59b8/leitfadenreihe_ratingmodelle_tcm14-11172.pdf (2. January 2016), Vienna, 2004
- S&P : see Standard and Poor's
- Scheule, H. (2003): Forecast of credit default risks , approved dissertation University of Regensburg, Uhlenbruch Verlag, Bad Soden / Ts., 2003
- Schwaiger, WSA (2002): Effects of Basel II on Austrian SMEs by industry and federal state , in Österreichisches Bankarchiv, 06/2002, pp. 433–446, 2002
- Standard and Poor's (Ed.) (2003b): Corporate Ratings Criteria , The McGraw Hills Companies, 2003
- Standard and Poor's (Ed.) (2005): Annual Global Corporate Default Study: Corporate Defaults Poised to Rise in 2005 , Global Fixed Income Research, The McGraw Hills Companies, 2005
- Sobehart, JR, Stein, RM, Mikityanska, V., Li, L. (2000): Moody's Public Firm Risk Model: A Hybrid Approach to Modeling Short Term Default Risk , Moody's Investors Service, Rating Methodology, Report # 53853, 03 / 2000
- Sobehart, JR, Keenan, SC, Stein, RM (2000): Benchmarking Quantitative Default Risk Models: A Validation Methodology , Moody's Investors Service, Rating Methodology, Report # 53621, http://www.rogermstein.com/wp-content/ uploads / 53621.pdf (January 2, 2016), 03/2000
- Somers, RH (1962): A new asymmetric measure of association for ordinal variables , American Sociological Review, Vol. 27 (6), pp. 799-811, 1962
- Standard and Poor's (Ed.) (2006): Annual 2005 Global Corporate Default Study And Rating Transitions , Global Fixed Income Research, The McGraw Hills Companies, 2006
- Stein, RM (2002): Benchmarking Default Prediction Models, Pitfalls and Remedies in Model Validation , Moody's KMV, Report # 030124, https://riskcalc.moodysrms.com/us/research/crm/validation_tech_report_020305.pdf (January 2, 2016 ), 2002
- Swets, JA (1988): Measuring the Accuracy of Diagnostic Systems , in Science, Vol. 240, pp. 1285-1293, 1988
- Treacy, WF, Carey, MS (2000): Credit Risk Rating at Large US Banks , in Journal of Banking and Finance, Vol. 24 (1-2), pp. 167-201, 2000