Braking power

Braking power of aluminum for protons as a function of the energy of the proton.

The braking capacity (English: Stopping Power ) of a material is the kinetic energy , which loses a charged particle per unit path length in penetrating the material, as measured, for example, in MeV / cm (see figure). The energy is consumed in various collision processes. The braking power depends on the type of particle, the current particle energy and the type and density of the material.

Braking power, Bragg peak and range

All electrically charged particles lose energy when passing through matter. In the following, mainly positive ions are considered. The term braking ability describes the situation from the standpoint of the braking material, so to speak, while energy loss per unit of path length relates to the particle. Both quantities are identical in terms of unit and numerical value. The energy loss per distance unit is usually written with a negative sign :

${\displaystyle S(E)=-{\mathrm {d} E \over \mathrm {d} x}}$

Bragg curve: energy loss per unit distance for 5.49 MeV alpha particles in air

where E is the energy and x is the path length. As a result of the minus sign, S is a positive quantity. Most of the time, the energy loss per unit of travel increases during the path that the particle travels. The curve that describes this is called the Bragg curve (named after William Henry Bragg ). Shortly before the end of the path, the energy loss per unit of travel passes through a maximum, the Bragg peak , and then drops abruptly to (almost) zero. This is of great practical importance in radiation therapy .

The above equation describes the linear braking power, which is measured in MeV / mm, for example. Dividing the linear braking capacity by the density of the material gives the mass braking capacity , which is measured, for example, in MeV / (mg / cm ² ). The mass braking capacity is independent of the material density.

The picture shows how the braking power of air - and thus also the ionization density - for alpha particles increases along the way until it reaches its maximum. 5.49 MeV is the energy of the alpha particles from the natural radon gas (Radon-222), which occurs wherever there is granite in the ground.

The distance that the particles travel until their energy drops to zero is called range . The range depends on the type of particle, the initial energy and the material. One can reach approximately ignoring the randomness of the energy output calculated by the reciprocal stopping power via the power (of the initial energy to zero) integrated (engl. Continuous slowing down approximation , CSDA):

${\displaystyle {\overline {R}}(E_{0})=\int _{E_{0}}^{0}{\frac {1}{S(E)}}\mathrm {d} E=\int _{E_{0}}^{0}-{\frac {\mathrm {d} x}{\mathrm {d} E}}\mathrm {d} E}$

The CSDA range calculated in this way must be distinguished from the depth of penetration into a medium. For light particles such as electrons, this is noticeably shorter than the “extended” CSDA range because the particles are deflected on their way by scattering at the atoms, resulting in a zigzag movement.

Bragg curves and photon absorption

The third picture shows the energy deposition of a proton beam of 250 MeV in water (orange curve); the curve has a very sharp Bragg peak. The blue curve shows the total energy deposition with several successive proton irradiations with varying energies. Such proton beams are used in the radiation therapy of extensive tumors, since here most of the energy deposition and thus also the damage takes place in the tumor itself.

For comparison, the picture also shows the absorption of a high-energy photon beam . This curve is completely different (essentially an exponential decrease), since the photon does not gradually release energy through many collisions, but mostly loses all of its energy in a single ionization process (see also radiation ). The absorption of a photon beam is not described by the braking power, but by an absorption coefficient .

The English expressions Stopping Power and Bragg-Peak are also very common in German.

Electronic and nuclear braking ability

Under electronic stopping power refers to the deceleration by inelastic collisions between the fast ion, and the electrons of the medium traversed. These collisions can cause excitation and ionization of both the electrons of the medium and the electrons of the ion.

The electronic braking capacity above a specific energy of a few hundred keV per nucleon can be calculated theoretically with an accuracy of a few percent, for example using the Bethe formula . The calculation becomes more difficult for lower energies.

Graphical representations of measured values ​​of the electronic braking capacity for many ions in many different substances are documented. The accuracy of various tables on braking power was examined with the help of statistical methods by Helmut Paul , among others .

Electronic and nuclear braking capacity of aluminum for aluminum ions, above the particle energy. The maximum of the nuclear braking capacity is typically at energies of around 1 keV per nucleon , the electronic braking capacity above 100 keV per nucleon

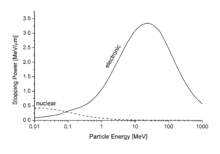
Under nuclear stopping power refers to elastic collisions between the ion and the atoms of the material (the term "nuclear" has nothing to do with nuclear forces, so nuclear forces). If one knows the shape of the repulsive potential between ion and atom, one can calculate the nuclear braking capacity . In the picture shown above for protons in aluminum, the nuclear contribution is negligible everywhere except for the smallest energy. However, as the mass of the ion increases, the nuclear contribution increases. In the figure shown here on the right, the nuclear contribution is greater than the electronic contribution at low energy. ${\displaystyle V(r)}$ ${\displaystyle S_{\mathrm {n} }(E)}$

At not too high energies the stopping power, therefore, is the sum of two quantities: . There are various semi-empirical models for calculating the braking power. The model by Ziegler, Biersack and Littmark was originally described in a book. The latest version of the program is used extensively today. ${\displaystyle S(E)=S_{\mathrm {e} }(E)+S_{\mathrm {n} }(E)}$

Beyond the maximum, the braking power decreases roughly proportionally with increasing speed , but increases again after passing through a minimum at relativistic speeds. Particles with this speed are called minimum ionizing particles (mip). ${\displaystyle 1/v^{2}}$ ${\displaystyle v}$

Grid guide effect (channeling)

→ Main article : Grid guide effect

Deviations from the usual braking power occur in monocrystalline solids. If the energies are not too small, the regular arrangement of the lattice atoms leads to a change in the collision probabilities, which then strongly depend on the direction of incidence of the particles relative to the orientation of the crystal.

Literature citations

1. ^ P. Sigmund, Particle Penetration and Radiation Effects . Springer Berlin Heidelberg New York, 2005
2. ↑ Helmut Paul: Stopping Power for Light and Heavier Ions - Graphs, Data, Comments and Programs , accessed on April 18, 2015.
3. ↑ Helmut Paul: A comparison of recent stopping power tables for light and medium-heavy ions with experimental data, and applications to radiotherapy dosimetry. In: Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. 247, 2006, pp. 166-172, doi : 10.1016 / j.nimb.2006.01.059 .
4. ↑ JF Ziegler, JP Biersack, and U. Littmark, The Stopping and Range of Ions in Matter, volume 1, Pergamon, New York, 1985.
5. ^ JF Ziegler: SRIM & TRIM
6. ^ JF Ziegler, JP Biersack, and MD Ziegler: SRIM - The Stopping and Range of Ions in Matter. SRIM Co., 2008. ISBN 0-9654207-1-X
7. ↑ http://pdg.lbl.gov/2005/reviews/passagerpp.pdf

Web links

• Passage of charged particles through matter, including plot (English; PDF file; 512 kB)

• Stopping power for protons and alpha particles (Engl.)

• Stopping Power: Data and Curves ( Memento from February 6, 2012 in the Internet Archive ) (English) This version is not up-to-date. For the current version s. o. under literature citations.