Chua circuit

The Chua circuit ( English Chua’s Circuit ) is an electronic circuit that was first introduced in 1983 by Leon. O Chua and published in 1984. The circuit shows chaotic behavior and is suitable as a demonstration object for effects of chaos theory and non-linear dynamics .

Electronic structure

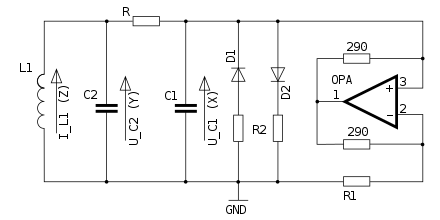
Circuit diagram of the Chua circuit.

The adjacent circuit diagram shows a Chua circuit. The operational amplifier OPA together with the two 290 ohm resistors and R1 forms a negative resistance with the value Together with the left circuit part, an oscillating circuit is formed. As far as the varying voltage exceeds the forward voltage of the diodes D1, D2 (in the positive as well as in the negative direction), the differential conductance increases ${\ displaystyle -R_ {1}.}$ ${\ displaystyle \ mathrm {d} I / \ mathrm {d} U}$ ${\ displaystyle 1 / R_ {2} -1 / R_ {1}.}$

The differential equation describing the system thus becomes non-linear and the dynamics of the system show the typical effects of chaotic systems , such as bifurcation and a strange attractor . The behavior of the present system is mostly described as a function of the value of the coupling resistance. ${\ displaystyle R}$

Theoretical description

Phase space of the dynamic system of a Chua circuit with a trajectory.

The circuit can be described with the help of Kirchhoff's rules . For this purpose, one chooses, for example, the voltages on the two capacitors and as well as the coil current as dynamic variables that span the phase space. The behavior of the non-linear resistor can be modeled with a function that reproduces its current-voltage characteristic. Please note that the same voltage is applied to the non-linear resistor as to the capacitor . ${\ displaystyle U_ {C_ {1}}}$ ${\ displaystyle U_ {C_ {2}}}$ ${\ displaystyle I_ {L_ {1}}}$ ${\ displaystyle g (U_ {C_ {1}})}$ ${\ displaystyle C_ {1}}$

By applying the nodal rule to the nodes across the two capacitors one gets

{\ displaystyle C_ {1} {\ frac {\ mathrm {d} U_ {C_ {1}}} {\ mathrm {d} t}} - {\ frac {U_ {C_ {2}} - U_ {C_ { 1}}} {R}} + g (U_ {C_ {1}}) = 0}

{\ displaystyle C_ {2} {\ frac {\ mathrm {d} U_ {C_ {2}}} {\ mathrm {d} t}} - {\ frac {U_ {C_ {1}} - U_ {C_ { 2}}} {R}} - I_ {L_ {1}} = 0}

From the rule of meshes we get

{\ displaystyle L_ {1} {\ frac {\ mathrm {d} I_ {L_ {1}}} {\ mathrm {d} t}} + U_ {C_ {2}} = 0}

This differential equation system characterizes the entire dynamics of the system. The solution to this is a trajectory in phase space , which, given the initial conditions, describes the evolution of the system over time, with the state of the system being given at any point in time by a point in phase space. Since the solution trajectory is unique, the behavior of Chua's circuit is strictly deterministic.

Individual evidence

↑ Wolfgang A. Halang (Ed.): Challenges through real-time operation: Real-time 2011 . Springer-Verlag, 2011, ISBN 3-642-24658-3 , p. 4 ( limited preview in Google Book search).
↑ Takashi Matsumoto: A Chaotic Attractor from Chua's Circuit . In: IEEE (Ed.): IEEE Transactions on Circuits and Systems . CAS-31, No. 12, December 1984, pp. 1055-1058. Retrieved May 1, 2008.

Web links

chuacircuits.com Schematics , equations, interactive simulations and images
Chua's circuit
NOEL - Berkeley

[1] Wolfgang A. Halang (Ed.): Challenges through real-time operation: Real-time 2011 . Springer-Verlag, 2011, ISBN 3-642-24658-3 , p. 4 ( limited preview in Google Book search).

[2] Takashi Matsumoto: A Chaotic Attractor from Chua's Circuit . In: IEEE (Ed.): IEEE Transactions on Circuits and Systems . CAS-31, No. 12, December 1984, pp. 1055-1058. Retrieved May 1, 2008.