Cluster coefficient

The clustering coefficient (engl. Clustering coefficient ) is in Graph theory , a measure of the formation of cliques and transitivity in a network . If all neighbors of a node are connected in pairs, i.e. each with each other, then they form a clique . This is synonymous with the concept of transitivity, because within a clique the following applies: If A is connected to B and A to C, then B and C are also connected. A distinction is made between the global cluster coefficient , which characterizes the entire network, and the local cluster coefficient , which characterizes an individual node.

Global cluster coefficient

Three nodes are connected to form a triangle at the top, three nodes form a “connected triple” at the bottom. The triangle has a global cluster coefficient of 1, since you count 1 triangle and 3 "connected triples"

The global cluster coefficient , also known as transitivity , is defined as the ratio of the number of triangles to “connected triples” in a network (see adjacent figure). ${\displaystyle C}$

${\displaystyle C={\frac {3\times {\text{Anzahl der Dreiecke}}}{\text{Anzahl der verbundenen Tripel}}}}$.

A triangle are three nodes that are all connected to each other. In contrast, a connected triple is a node A and a disordered pair of two nodes B and C, where A has edges to B and C. Each triangle thus forms 3 connected triples. The factor 3 in the numerator of the formula compensates for this. A network consisting of a single triangle receives the cluster coefficient only with a factor of 3 , which corresponds to a perfect clique. ${\displaystyle C=1}$

Local cluster coefficient

The local cluster coefficient of a node in a graph , defined by Duncan Watts and Steven Strogatz , denotes in graph theory the quotient of the number of edges that actually run between its neighbors ( ) and the number of edges that could maximally run between these neighbors ( undirected graph :) : ${\displaystyle i}$ ${\displaystyle G}$ ${\displaystyle k_{i}}$ ${\displaystyle =n}$ ${\displaystyle {\tfrac {1}{2}}k_{i}(k_{i}-1)}$

${\displaystyle C_{i}={\frac {2n}{k_{i}(k_{i}-1)}}.}$

This formula applies to an undirected graph; the factor 2 does not apply to a directed graph, since twice as many edges are possible between the neighbors as in an undirected graph.

Six node graph

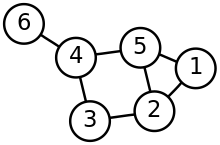
In the graph opposite, node 1 has neighbors 2 and 5. Between these neighbors, an edge is possible and also present, so that the cluster coefficient is. The node 2 has 3 neighbors, between which 3 edges are possible, but only the neighboring nodes 1 and 5 are connected by an edge. The cluster coefficient is therefore . According to the calculation, the cluster coefficient of node 6, i.e. all nodes of degree 1, results in division zero by zero. In some implementations this is implemented with the value 1; with many nodes of this type an unnaturally high global cluster coefficient results. Other authors define the local cluster coefficient for isolated nodes and nodes of degree 1 . With the last-mentioned convention, the following local cluster coefficients up to : ${\displaystyle C_{1}=1}$ ${\displaystyle C_{2}}$ ${\displaystyle {\tfrac {1}{3}}}$ ${\displaystyle C_{i}=0}$ ${\displaystyle C_{1}}$ ${\displaystyle C_{6}}$

${\displaystyle 1,{\frac {1}{3}},0,0,{\frac {1}{3}},0}$.

The local cluster coefficient can also be equivalent as

${\displaystyle C_{i}={\frac {{\text{Anzahl der Dreiecke verbunden mit Knoten }}\,i}{{\text{Anzahl der „verbundenen Tripel“ zentriert an Knoten }}\,i}}}$

To be defined.

The mean of all local cluster coefficients is often referred to as the global cluster coefficient:

${\displaystyle C'={\frac {1}{N}}\sum _{i}^{N}C_{i}}$.

This definition does not return the same value as the first definition of the global cluster coefficient ; the order of calculation of the triangle-to-triple ratio on the one hand and the averaging on the other hand is reversed. The difference is effectively the reverse of the operations of calculating the ratio of triangles and triples and averaging: the latter definition is the mean of the triangle-to-triple ratio, the former in some way calculates the ratio of the mean number of triangles to the mean Number of triples. Both definitions and can deliver very different results: For the network shown, and . ${\displaystyle C}$ ${\displaystyle C'}$ ${\displaystyle C={\tfrac {3}{11}}}$ ${\displaystyle C'={\tfrac {5}{18}}}$

${\displaystyle C'}$ is easier to calculate on the computer, so it is widely used in numerical studies.

Small world networks - regardless of the definition chosen - usually have high cluster coefficients, whereas random graphs tend to have low ones .

See also

• Cluster analysis
• Networking

Web links

Commons : Clustering coefficient  - collection of images, videos and audio files

swell

1. ↑ ^{a b c d e} M. EJ Newman: The Structure and Function of Complex Networks , SIAM Review 45 , 167 (2003), p. 183
2. ↑ ^{a b} p Boccaletti, V. Latora, Y. Moreno, M. Chavez, and DU Hwang: Complex Networks: Structure and Dynamics, Physics Reports 424 , 175 (2006)
3. ^ DJ Watts and Steven Strogatz : Collective dynamics of 'small-world' networks . In: Nature . 393, No. 6684, June 1998, pp. 440-442. bibcode : 1998Natur.393..440W . doi : 10.1038 / 30918 . PMID 9623998 .