De Morgan's Laws
The de-morgan's laws (and often de-Morganist rules ) are two basic rules for logical statements. They were named after the mathematician Augustus De Morgan , although they were already known to the medieval logician Wilhelm von Ockham . They apply in all Boolean algebras . They are particularly important in propositional logic and set theory . In technology, they are important for creating interlocks and programs.
Laws
In logic they are :
- not (a and b) is equivalent to ((not a) or (not b))
- not (a or b) is equivalent to ((not a) and (not b))
In mathematics, one can find numerous different representations of the De Morgan laws of propositional logic :
- or with a different notation:
The validity of De Morgan's laws can be proven using truth tables .
Its equivalent in set theory is (where A is the complement of A , the symbol for the intersection of two sets and the symbol for the union of two sets):
The rules can also be extended to link any number of elements. So for any finite, countable or non-countable index set I :
- and .
Inferences
A conjunction (AND link) can be represented by three negations and a disjunction (NOT or OR links) with the help of De-Morgan's law :
Accordingly, a disjunction can be represented by three negations and a conjunction:
application
The de-morgan's laws have important applications in discrete mathematics , the electrical , the physics and computer science . In particular, the de-morgan's laws are in the design of digital circuits used to the types of logic used switching elements replaced with another or to save components.
Examples
Example from everyday life
Suppose a person likes to drink coffee: To express that he only drinks it black and without sugar, he can make the following statements:
- If there is milk or sugar in it, then I will not drink the coffee.
Converted from de Morgan and counterposition :
- When I drink the coffee, there is no milk or sugar in it.
Both statements are of equal value.
Example in set theory
It's supposed to be based on the relationship
the validity of De Morgan's rules are illustrated. There are two sets A and B, which are subsets of a superset Ω. The graph 1 shows the location of the quantities and its counter quantities A and B .
Figure 2 shows how it is formed. Figure 3 shows the complement to , and you can see that both sets are equal.

|
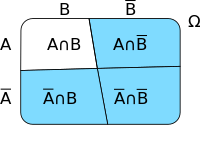
|

|
| Division of the superset into A and B. |
One interpretation would be:
In an acceptance test, high-quality chef's knives are checked to see whether the cutting edge is free of defects (quantity A) and whether the cutting edge is properly anchored in the handle (quantity B). A knife is not accepted, if there is the amount A or the amount of B is one or two, that is, when at least one complaint is present: . The knife is accepted if it fulfills both requirements, that is, if it belongs to the crowd , that is, it is not accepted if it belongs to.














