Equation xʸ = yˣ

Non-negative pairs of solutions to the equation ${\displaystyle x^{y}=y^{x}}$

In general, the exponentiation of two real numbers is not commutative . The equation still has an infinite number of solutions. One solution is . ${\displaystyle x^{y}=y^{x}}$ ${\displaystyle x=2,\,y=4}$

history

The equation is mentioned in a letter from Daniel Bernoulli to Christian Goldbach on June 29, 1728. The letter contains the statement that the only two solutions of the above equation, where natural numbers should be, or are. Goldbach's answer of January 31, 1729 contains general solutions to the equation obtained by the substitution . A similar solution was found by Leonhard Euler . ${\displaystyle x^{y}=y^{x}}$ ${\displaystyle x\neq y}$ ${\displaystyle x=2,y=4}$ ${\displaystyle x=4,y=2}$ ${\displaystyle y=tx}$

J. van Hengel pointed out that for natural numbers and the following applies: . So it is enough to consider and to find all solutions for natural numbers. ${\displaystyle r\geq 3}$ ${\displaystyle n}$ ${\displaystyle r^{r+n}>(r+n)^{r}}$ ${\displaystyle x=1}$ ${\displaystyle x=2}$

The problem has been addressed in several publications. In 1960 the equation appeared in the William Lowell Putnam Competition , which led Alvin Hausner to extend the results to algebraic number fields .

Non-negative real solution pairs

Main source:

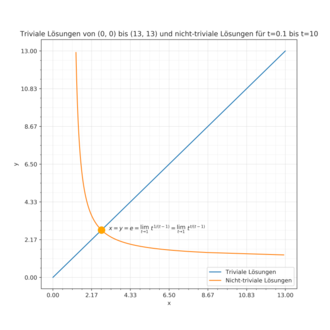
An infinite set of “trivial” solutions is given by the condition . ${\displaystyle x=y}$

So we are looking for non-negative solution pairs ( ) for which holds. It can be assumed that the only trivial solution for which or holds is is. So we can write for exactly one t , where holds. The equation is now: ${\displaystyle x,y\geq 0}$ ${\displaystyle x\neq y}$ ${\displaystyle x,y>0}$ ${\displaystyle x=0}$ ${\displaystyle y=0}$ ${\displaystyle x=y=0}$ ${\displaystyle y=tx}$ ${\displaystyle t>0,t\neq 1}$

${\displaystyle (tx)^{x}=x^{tx}=(x^{t})^{x}}$.

Applying the -th root and dividing by on both sides gives: ${\displaystyle x}$ ${\displaystyle x}$

${\displaystyle t=x^{t-1}}$.

Since is by definition , all non-negative, non-trivial solution pairs can be written as follows ( ): ${\displaystyle y=tx}$ ${\displaystyle t>0,t\neq 1}$

${\displaystyle x=t^{1/(t-1)}}$,

${\displaystyle y=t^{t/(t-1)}}$.

In addition, there are solutions to the equation for all of the above pairs. If, for example , one sets or , one obtains the above solution . ${\displaystyle t>0}$ ${\displaystyle t=2}$ ${\displaystyle t={\tfrac {1}{2}}}$ ${\displaystyle 4^{2}=2^{4}}$

Other pairs of solutions that consist of algebraic numbers are, for example, and , as well as and . ${\displaystyle {\sqrt {3}}}$ ${\displaystyle 3{\sqrt {3}}}$ ${\displaystyle {\sqrt[{3}]{4}}}$ ${\displaystyle 4{\sqrt[{3}]{4}}}$

The intersection of the curve im belonging to the above solutions and the curve lies at (with continuous continuation ) . In this case it is ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle x=y}$ ${\displaystyle t=1}$

${\displaystyle x=\lim _{t\to 1}t^{1/(t-1)}=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}=e}$.

So the intersection is included . ${\displaystyle x=y=e}$

Web links

• Rational Solutions to x ^ y = y ^ x . In: CTK Wiki Math .
• x ^ y = y ^ x - commuting powers . In: Arithmetical and Analytical Puzzles . Torsten Sillke. Archived from the original on December 28, 2015.
• dborkovitz: Parametric Graph of x ^ y = y ^ x . GeoGebra . January 29, 2012.
• Follow A073084 in OEIS

Individual evidence

1. ^ Leonard E. Dickson : History of the Theory of Numbers . tape II . Washington 1920, p. 687 ( google.com ).
2. ^ ^{A b c d} Marta Sved: On the Rational Solutions of x ^y = y ^x Archived from the original on March 4, 2016. In: Mathematics Magazine . 1990.
3. ↑ ^{a b} Lajos Lóczi: On commutative and associative powers Archived from the original on October 15, 2002. In: KöMaL . September. Translation of: Mikor kommutatív, illetve asszociatív a hatványozás? ( hu ) Archived from the original on May 6, 2016.
4. ^ ^{A b c} David Singmaster : Sources in recreational mathematics: an annotated bibliography. 8th preliminary edition . Archived from the original on April 16, 2004.
5. ↑ Johann van Hengel: proof of the theorem that among all real positive integers only the pair of numbers 4 and 2 for a and b of the equation a ^b = b ^a suffices . In: Report on the Royal High School in Emmerich . 1888.
6. ^ Andrew Gleason , RE Greenwood, Leroy Milton Kelly: The William Lowell Putnam mathematical competition problems and solutions: 1938-1964 . Ed .: MAA . 1980, ISBN 0-88385-428-7 , pp. 59 ( google.com ).
7. ^ Algebraic Number Fields and the Diophantine Equation m ⁿ = n ^m . In: The American Mathematical Monthly . November 1961.