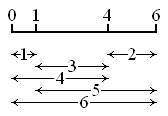
Golomb ruler

from Wikipedia, the free encyclopedia
Demonstration of how a conference room can be configured with the proportions of the Golomb ruler [0, 2, 7, 8, 11] in 10 different sizes.

A Golomb ruler or Golomb ruler (often also Golomb Ruler after the English technical term) is a ruler in number theory in which there are no two markings at integer positions with the same distance from one another.

Golomb ruler of order 4 and length 6 which is both optimal and perfect .

Golomb rulers get their name from Solomon W. Golomb , a US professor of mathematics and electrical engineering at the University of Southern California .

Golomb rulers are categorized based on their order and length. The order of a Golomb ruler is defined by the number of marks, the length by the greatest distance between two marks. Since parallel shifting and mirroring are viewed as trivial operations with Golomb rulers, the smallest marking is usually set to 0 and the following marking to the smaller of the two possible positions.

It is not necessary that a Golomb ruler can measure all distances up to its length, so that all distances between all markings - in ascending order - result in a complete series of numbers (1,2,3,4,5, ...). However, when it does, it's called a perfect Golomb ruler. A Golomb ruler is optimal when there are no shorter rulers of the same order. Finding optimal Golomb rulers for a given order is a computationally intensive task, as opposed to creating Golomb rulers. So far, optimal Golomb rulers up to order 27 have been confirmed by the distributed.net project by means of distributed computing . The follow-up project for Order 27 confirmed the shortest known ruler to date after a total duration of almost five years. The search for an optimal 28-order ruler was started in February 2014, and a processing time similar to that of the previous project is expected.

application

Golomb rulers are used in the design of array antennas such as radio telescopes . Antennas in a [0,1,4,6] Golomb arrangement are often found on cell phone masts . The arrangement of field sensors in magnetic resonance imaging also uses properties of Golomb scales.

In both applications, the aim is to achieve a maximum number of different distances with a minimum number of elements (antennas, sensors) and, in three-dimensional terms, a maximum number of different emission and reception angles. If the Golomb rulers used are optimal, the expansion of the measuring system or the group antenna is also minimized, which improves manageability or enables use in the first place.

Known optimal Golomb rulers

The table shows the values ​​for all currently known optimal Golomb rulers up to order 27, with equivalent rulers (that is, in reverse order to one of the specified ones) are not included. The first four represent perfect Golomb rulers.

order length Markings
1 0 0
2 1 0 1
3 3 0 1 3
4th 6th 0 1 4 6
5 11 0 1 4 9 11
0 2 7 8 11
6th 17th 0 1 4 10 12 17
0 1 4 10 15 17
0 1 8 11 13 17
0 1 8 12 14 17
7th 25th 0 1 4 10 18 23 25
0 1 7 11 20 23 25
0 1 11 16 19 23 25
0 2 3 10 16 21 25
0 2 7 13 21 22 25
8th 34 0 1 4 9 15 22 32 34
9 44 0 1 5 12 25 27 35 41 44
10 55 0 1 6 10 23 26 34 41 53 55
11 72 0 1 4 13 28 33 47 54 64 70 72
0 1 9 19 24 31 52 56 58 69 72
12 85 0 2 6 24 29 40 43 55 68 75 76 85
13 106 0 2 5 25 37 43 59 70 85 89 98 99 106
14th 127 0 4 6 20 35 52 59 77 78 86 89 99 122 127
15th 151 0 4 20 30 57 59 62 76 100 111 123 136 144 145 151
16 177 0 1 4 11 26 32 56 68 76 115 117 134 150 163 168 177
17th 199 0 5 7 17 52 56 67 80 81 100 122 138 159 165 168 191 199
18th 216 0 2 10 22 53 56 82 83 89 98 130 148 153 167 188 192 205 216
19th 246 0 1 6 25 32 72 100 108 120 130 153 169 187 190 204 231 233 242 246
20th 283 0 1 8 11 68 77 94 116 121 156 158 179 194 208 212 228 240 253 259 283
21st 333 0 2 24 56 77 82 83 95 129 144 179 186 195 255 265 285 293 296 310 329 333
22nd 356 0 1 9 14 43 70 106 122 124 128 159 179 204 223 253 263 270 291 330 341 353 356
23 372 0 3 7 17 61 66 91 99 114 159 171 199 200 226 235 246 277 316 329 348 350 366 372
24 425 0 9 33 37 38 97 122 129 140 142 152 191 205 208 252 278 286 326 332 353 368 384 403 425
25th 480 0 12 29 39 72 91 146 157 160 161 166 191 207 214 258 290 316 354 372 394 396 431 459 467 480
26th 492 0 1 33 83 104 110 124 163 185 200 203 249 251 258 314 318 343 356 386 430 440 456 464 475 487 492
27 553 0 3 15 41 66 95 97 106 142 152 220 221 225 242 295 330 338 354 382 388 402 415 486 504 523 546 553

Web links

Individual evidence

  1. ^ Paul Erdős , Paul Turan : On a problem of Sidon in additive number theory, and on some related problems. In: J. London Math. Soc. 16: 212-215, 1941.
  2. ↑ http://blogs.distributed.net/2014/02/25/16/09/mikereed/
  3. ↑ http://blogs.distributed.net/2014/02/18/23/23/mikereed/