Hyperbolic fixed point

A hyperbolic fixed point is a fixed point (also called equilibrium point ) of a dynamic system with certain properties. In contrast to an elliptical fixed point, there are no center manifolds on which the solution curves called orbits circle the fixed point, but rather unstable and stable manifolds on which the orbits approach the fixed point (stable manifold) or move away from it (unstable manifolds). The classification of fixed points plays a role in the qualitative discussion of the solutions of systems of ordinary differential equations (see the article Autonomous Differential Equation ).

Phase portrait near a typical hyperbolic fixed point, a saddle point

The name comes from the fact that in the case of two-dimensional autonomous differential equation systems , which are often used to describe dynamic systems, the phase flow in the typical case of a saddle point is hyperbolic -like (see figure). The intersecting straight lines in the figure (the separatrix) are the stable manifold (the straight line where the arrows point towards the fixed point in the center) and the unstable manifold (straight line on which the arrows point away from the fixed point). Alternatively, this can also be explained using the eigenvalue structure of the linearized systems around the fixed point:

In the case of autonomous systems of differential equations, one considers the solution curves of the differential equation , which define a phase flow (a vector field). If you linearize around a fixed point for which is, you get a linear mapping with the Jacobian matrix (matrix of partial derivatives) . A hyperbolic fixed point exists if none of its eigenvalues has the real part 0. Then it can be shown for two dimensions that either the two eigenvalues are real and have opposite signs (one also speaks of a saddle point ), or both have the same sign of the real part (unstable nodes (sources) with positive signs and stable nodes ( Lowering) with a negative sign if the imaginary part disappears and otherwise stable and unstable foci, geometric spirals). In the case of conservative systems that is often considered, hyperbolic fixed points in the plane are only concerned with saddle points. Under general conditions it can be shown that locally a stable and / or an unstable manifold (both invariant under the flow) of the fixed point exist, which can also disappear or are of full dimension of the underlying space as with sources and sinks (stable- Manifold Theorem). According to Hartman-Grobman's theorem , the behavior around the hyperbolic fixed point in the linearized system is topologically similar ( locally topologically conjugated ) to that of the full, possibly non-linear system. This expresses the structural stability of the behavior of dynamic systems around hyperbolic fixed points (in contrast to elliptical fixed points). ${\ displaystyle {\ vec {x}} (t)}$ ${\ displaystyle {\ vec {x}} _ {t} = F ({\ vec {x}})}$ ${\ displaystyle p}$ ${\ displaystyle {\ vec {x}} _ {t} = F ({\ vec {x}}) = 0}$ ${\ displaystyle {\ vec {u}} _ {t} = A {\ vec {u}}}$ ${\ displaystyle A}$ ${\ displaystyle \ mathbb {R} ^ {n}}$

One can the dynamic system as a discrete dynamic system of pictures ( diffeomorphisms conceive) . A hyperbolic fixed point of the diffeomorphism is a fixed point p ( ), at which the Jacobi matrix has no eigenvalues with magnitude 1 (which are therefore on the unit circle). The connection with the definition via vector fields results from the fact that the vector flow integrated over time is considered in the case of images, so that the eigenvalues from there correspond to the eigenvalues of : if the real part of the eigenvalues of A disappears, this corresponds to the modulus 1. An example for a picture that has only one hyperbolic fixed point is Arnold's cat picture . 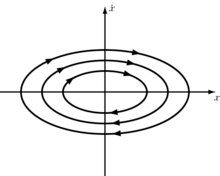${\ displaystyle T: \ mathbb {R} ^ {n} \ to \ mathbb {R} ^ {n}}$ ${\ displaystyle T ^ {k} (p) = p}$ ${\ displaystyle DT (p)}$ ${\ displaystyle A}$ ${\ displaystyle e ^ {A}}$ ${\ displaystyle e ^ {A}}$

With elliptical fixed points the real part of the eigenvalues vanishes, which are then purely imaginary (i.e. have modulus 1) and the flow around the fixed point can be described as a rotation (with a center manifold).

Hyperbolic fixed points often lead to chaotic movement (see homoclinic orbit ).

Elliptical fixed point: periodic movement around a center

example

The nonlinear two-dimensional system of ordinary autonomous differential equations

{\ displaystyle {\ frac {\ mathrm {d} x} {\ mathrm {d} t}} = y,}

{\ displaystyle {\ frac {\ mathrm {d} y} {\ mathrm {d} t}} = - xx ^ {3} - \ alpha y, ~ \ alpha \ neq 0}

has the only fixed point . Linearization around the fixed point results in the Jacobian matrix ${\ displaystyle (x, y) = (0,0)}$

{\ displaystyle J (0,0) = {\ begin {pmatrix} 0 & 1 \\ - 1 & - \ alpha \ end {pmatrix}}}

.

with the eigenvalues . For all of them these have non-vanishing real parts and one is therefore dealing with a hyperbolic fixed point. According to Grobman-Hartman's theorem, the system behaves like the linearized form in the non-linear case near the fixed point and the behavior is similar to the first figure above. ${\ displaystyle {\ frac {- \ alpha \ pm {\ sqrt {\ alpha ^ {2} -4}}} {2}}}$ ${\ displaystyle \ alpha \ neq 0}$

Web links

Eugene Izhikevich, Equilibrium, Scholarpedia

Individual evidence

↑ See autonomous differential equation

[1] See autonomous differential equation