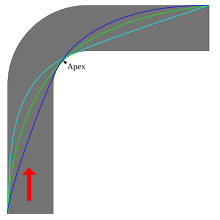
Ideal line
The ideal line is an imaginary line that describes the fastest possible route on a racetrack . However, this can be different for different vehicles or driving styles. Different setups sometimes require different fastest lines.
Every race track has several characteristic ideal lines on which the track can be bypassed at the highest average speed, depending on the prevailing general conditions . The general conditions to be considered are the setup and the grip as well as the track and weather conditions, such as wetness, dryness and temperature. There is no generally applicable ideal line for any racetrack that would apply to every vehicle and every weather condition.
In simple terms, the ideal line is the line which, under the given conditions, leads through a curve fastest. The ideal line of a combination of curves can deviate from the ideal lines of the individual curves. There are also several possible ideal lines for some types of curves, even under the same conditions.
The racing line is rarely the shortest route through a curve. The strategy of the fastest line is rather to increase the curve radius and to accelerate out of the curve as early as possible. Such a curve is usually braked outside , is deflected late at the vertex ( apex approached) inward and then used the road width to let out port to the vehicle under acceleration. In the duel of the front man often chooses the place of the ideal line to defend its position battle line .
When the ground is wet, the “rain line” is usually chosen in such a way that a wide arc is driven, avoiding rubber abrasion at the apex. In addition, the outer edge of the curve dries faster due to a slight elevation, as the water, following the slope, flows to the inner edge.
In other sports there are ideal lines, such as when skiing or bicycle racing and marathon running .
Curve cutting
If the driver leaves his own lane when driving through a bend, this is known as cornering . The radius of curvature when driving through the curve normally is r 1 . The relationship between the maximum speed with which one can drive through a curve and the radius of curvature r applies
- .
Cutting a curve increases the radius of curvature to r 2 ; so you can drive faster through the curve. However, if you have to swerve suddenly in oncoming traffic, the radius of curvature r 3 is so small that the car can no longer be controlled.
Cutting corners is a violation of the right-hand driving law .