Ionospheric dynamo layer

from Wikipedia, the free encyclopedia

The ionospheric dynamo layer , an area in the earth's atmosphere , is located between about 85 and 200 km altitude and is characterized by an electrically conductive ionospheric plasma, which is moved by solar and lunar atmospheric tides against the lines of force of the earth's magnetic field , thereby inducing electric fields and currents , just like the moving coil in a technical dynamo that moves against a magnetic field. The magnetic field of such currents is measured on the earth's surface as a fluctuation in the earth's magnetic field. These variations are called Sq variations (S = solar ; q = quiet ) and L variations (l = lunar ). The tides themselves are caused by different levels of solar radiation in the atmosphere or by the gravitational influence of the moon.

A varying magnetospheric convection electric field creates additional electric currents within the ionospheric dynamo layer, the DP1 (the polar electric jets) and the DP2 currents. Furthermore, there is a polar ring current that depends on the interplanetary magnetic field. Such geomagnetic variations belong to the geomagnetic external field, the amplitudes of which rarely reach 1% of the internal main field B o .

Atmospheric electrical conductivity

Radioactive gas from the earth's interior and galactic cosmic radiation ionize a small part of the air within the lower and middle atmosphere and make the neutral gas electrically conductive. Electrons combine very quickly with neutral gas particles and form negative ions. The ions are usually monatomic. The electrical conductivity depends on the mobility of the ions. This mobility is proportional to the reciprocal air density and therefore increases exponentially with altitude. The ions move with the neutral gas, so that the electrical conductivity is isotropic but extremely small.

In the altitude range between about 85 and 200 km - the dynamo layer - the solar X-ray and extreme ultraviolet radiation (XUV) are almost completely absorbed and the air is partially ionized. The different ionospheric layers arise . In this altitude range the electrons are already bound to the earth's magnetic field and gyrate around the magnetic field lines several times before they collide with neutral gas particles. The ions, on the other hand, essentially move with the neutral gas. The result is anisotropic electrical conductivity. The conductivity parallel to the electric field E is called Pedersen's conductivity. Pedersen currents have ohmic losses and thus generate Joule heating. The conductivity perpendicular to E and to the earth's magnetic field B o is the Hall conductivity. The component parallel to B o (parallel conductivity) continues to grow with height. In the vicinity of the Earth's magnetic equator, a west-east electric field creates a vertical Hall current that is not closed. This creates a vertical polarization field that generates a horizontal Hall current. This additional Hall current amplifies the Pedersen current. Such reinforcement is described by the cowling conductivity. Pedersen and Hall conductivity reach a maximum in about 120 to 140 km. During the day they have numerical values ​​of approx. 1 mS / m. At night, these values ​​can drop to a tenth. The conductivity values ​​depend on the time of day, latitude, season and the sun's eleven year cycle. The height-integrated conductivities are of the order of magnitude of 50 S or have a resistance of approx. 0.02 ohms.

In the polar light zones, which are located at approx. 70 ° to 75 ° north and south geomagnetic latitude, high-energy particles from the magnetosphere penetrate, which additionally ionize the air at a height of approx. 110 to 120 km and thus increase the Pedersen and Hall conductivity . This conductivity increases during strong geomagnetic disturbances.

Above about 200 km, the collisions between neutral gas and plasma become increasingly rare, so that both positive ions and electrons can only gyrate around the magnetic field lines or drift perpendicular to E and B o . The parallel conductivity becomes so great that the geomagnetic field lines become electrical equipotential lines. So only electric fields can exist orthogonally to B o (see magnetosphere ).

Atmospheric tides

Atmospheric tides are large-scale atmospheric waves that are excited by regular differential solar radiation (solar tides) or by the gravitational influence of the moon (lunar tides). The atmosphere behaves like a giant waveguide that is closed at the bottom (on the ground) and open at the top. An infinitely large number of natural waves (wave modes) can be generated in such a waveguide. The waveguide is not perfect, however, so that only waves with large horizontal and vertical dimensions develop enough to be filtered out of the meteorological noise. These waves are solutions to Laplace's equation . They are called Hough functions and can be approximated using spherical functions .

There are two types of wave types: Class I waves (also called gravitational waves) and Class II waves (rotational waves). Class II waves exist only because of the Coriolis force and disappear for periods less than 12 hours. The eigenwaves are either internal waves with finite vertical wavelengths that can transport wave energy upwards, or external waves with infinitely large vertical wavelengths whose phases are constant with height. The amplitudes of internal waves grow exponentially with height. External waves, on the other hand, cannot transport wave energy, and their amplitudes decrease exponentially with height outside their source area. Every wave mode is characterized by four numbers: by the zonal wave number n, the meridional wave number m (the meridional structure of the waves becomes more and more complex with increasing m), by their eigenvalue (also called equivalent depth based on ocean tides), and by their period , in the case of tides 12 hours (half-day waves) and 24 hours (all-day waves) etc. The modes are identified by the number duo (n, m). Even numbers of n apply to symmetric waves with respect to the equator, odd numbers of n to antisymmetric waves. Class II waves are characterized by negative values ​​of n.

In the altitude range above about 150 km, all waves develop into external waves and the Hough functions degenerate into spherical functions. For example, the wave mode (1, -2) becomes the spherical function P 1 1 (θ), mode (2, 2) becomes P 2 2 (θ) etc. with θ the pole distance etc.

Wandering solar tides

The fundamental all-day tidal wave, which optimally fits the meridional structure of the solar radiation and is therefore most strongly stimulated, is the mode (1, −2). It is a class II external wave and travels westward with the sun. Its maximum pressure amplitude on the ground is 60 Pa. However, this wave becomes the dominant mode in the thermosphere and reaches temperature amplitudes of the order of 100 K and wind speeds of 100 m / s and more in the exosphere .

The strongest half-day wave has the identifier (2, 2). It is an internal class I wave and has a maximum pressure amplitude on the ground of 120 Pa. This amplitude increases with altitude. Although its solar excitation energy is only half as large as that of the all-day wave (1, -2), its amplitude on the ground is twice as large. This indicates the suppression of an external wave compared to an internal wave.

Half day lunar tides

The dominant lunar tidal wave is the mode (2, 2). It depends on the local lunar day. Its maximum pressure amplitude on the ground is 6 Pa. Such a tiny amplitude can only be filtered with difficulty from the meteorological noise. This mode is an internal wave, the amplitude of which increases exponentially with altitude and is two orders of magnitude larger at a height of 100 km than on the ground.

Electric currents

Sq stream

morphology

More than 100 geomagnetic stations on earth regularly measure the variations in the earth's magnetic field. The daily variations during selected calm terrestrial magnetic activity are used to form a monthly mean. An equivalent electric current J in the ionospheric dynamo layer can be derived from the horizontal component of this mean value ΔH. His strength is

J = 2 ΔH / µ = 1.6 ΔH

where J (in milliamps per meter) is the electric current in an infinitely thin layer at an altitude of about 120 km, ΔH (in nanotesla) is the observed horizontal component of the geomagnetic variation and μ is the permeability of free space. The direction of the magnetic field in relation to the electric current can be determined with the right-hand rule . If the right thumb points in the direction of the current, then the magnetic field is directed in the direction of the curved fingers.

One has to take into account that this relationship is not clear. In general, the electrical currents within the ionosphere and magnetosphere are three-dimensional, and an infinite number of current configurations match the magnetic field measured on the ground. Magnetic field measurements far above the earth's surface are therefore necessary to obtain a clear picture.

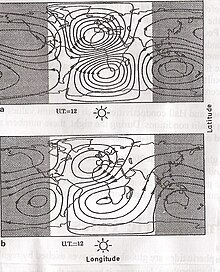
Figure 1. Streamlines of the equivalent ionospheric Sq current during the equinoxes (1957–1969) separated by 12 UT into primary current (a) and secondary current (b). 20 kA flow between two streamlines

Figure 1a shows the streamlines of the equivalent electrical Sq current, viewed from the sun. A total current of 140 kA flows in each daily current vortex.

The rotating Sq current and the electrically conductive interior of the earth behave like a huge transformer with the dynamo layer as the primary winding and the earth as the secondary winding. Since the Sq current moves with a period of one day, a secondary current is induced in the earth's interior, the magnetic field of which is superimposed on the primary field. Figure 1b shows this secondary current as seen from the sun. The magnetic field amplitudes of this secondary current system are about a third of the primary field. That actually means the relationship between primary current and magnetic field

J ≈ ΔH

is. The strength of the Sq current depends on the time of year. The summer vortex is stronger than the winter vortex. A length dependency exists due to the inclined earth's magnetic field in relation to the earth's axis. But non-migrating internal tidal waves that penetrate the dynamo layer can also generate variations in the Sq current. During the 11-year cycle of solar activity, the amplitude of the Sq current can change by a factor of two or more. Two thirds of this fluctuation can be explained by the change in conductivity in the course of fluctuating solar activity. The rest may depend on the solar wind fluctuation. During the night the electron density of the ionospheric E-layer decreases. Therefore the center of the dynamo layer moves upwards.

The main generator of the Sq-Current is the external all-day tidal wave (1, −2). Since their phase is constant with altitude, their altitude-independent coherent wind system is particularly effective, while the winds of the internal waves interfere destructively. A Fourier analysis shows that there is a half-day component that has an amplitude of about 1/2 the amplitude of the full-day component, out of phase by 180 °. This appears to be the result of a non-linear coupling between all day varying wind and all day varying conductivity. The center of the vortex shows a day-to-day variability. This is the result of the effect of internal tidal waves as well as of meteorological conditions, but also the effect of solar activity

A strong beam current, about four times larger than the Sq current in mid-latitudes, is observed within the range of about ± 150 km from the geomagnetic equator. This is caused by the influence of the cowling conductivity in the vicinity of the equator.

During a solar flare , increased solar radiation reaches the iononospheric D and E layers on the day side. This increases the electrical conductivity, which becomes noticeable as a small bulge in the geomagnetic variation (geomagnetic solar flare effect, also known as crochet ). During a solar eclipse, the opposite happens in the shadow area. The conductivity is lowered and a slight decrease in the geomagnetic variation is observed (solar eclipse effect of the earth's magnetic field). Both effects can only be observed in geomagnetically calm conditions.

As a strong geomagnetic storm subsides, a type of anti-Sq current called Ddyn develops for a short time. It is generated by Joule heating in the polar ionospheric dynamo layer.

theory

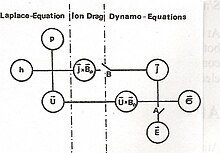
Figure 2. Block diagram that illustrates the coupling between horizontal wind U and pressure p via ampere force j × B o , and Lorentz force U × B o . j is the electrical current density, B o is the earth's magnetic field, h is the equivalent depth, σ is the electrical conductivity and E is the electrical polarization field. Gate B must be closed for a complete calculation of the coupled system. Gate B remains open in conventional dynamo theories.

In order to quantitatively calculate the dynamo effect of the tidal wind, one starts from the horizontal components of the moment equation ( Laplace equation ) together with an equation for the divergence of the wind. In the Laplace equation, the inertial force , the Coriolis force , the horizontal pressure gradient and the ampere force j × B o are in equilibrium. The ampere force couples the electrical current density j to the wind and pressure system. The electric current j obeys Ohm's law. An electrical polarization field E is caused by charge separation and ensures that the electricity system is free from divergence. The feedback between the wind and the electric current takes place via the Lorentz force U × B o . In general, the electrical conductivity tensor is σ by a height-integrated conductivity tensor Σ and the current density j by a height-integrated surface current J replaced.

In conventional dynam theories, the ampere force is neglected. This means that gate B in Figure 2 is open. This is called a kinematic dynamo. Closed gate B models are called hydromagnetic dynamos. The influence of the mutual coupling between wind and electrical current can be seen immediately if one assumes an infinitely high electrical conductivity. In the kinematic model, the electric current would be infinitely large, but the wind would remain unaffected. In the hydromagnetic model, on the other hand, the electric current reaches a maximum, similar to a technical dynamo in the event of a short circuit, while the wind drops to a minimum value. Charge separation acts like a self-impedance that prevents the electric current from growing indefinitely.

L current

The lunar (L) current is weaker than the Sq current by a factor of about 20. It behaves similarly to the Sq stream with the difference that there are four instead of two current vortices. In each current vortex, an average total current of approx. 4 kA flows. Its seasonal fluctuations are also similar to those of the Sq current. During the day the L-current is increased. He is very small at night. So there is a modulation that depends on the lunar phase. The geomagnetic effect of the L-current is particularly clearly visible in the area of ​​the geomagnetic equator, where the cowling conductivity allows this current to increase significantly.

DP1 stream

The action of the solar wind on the magnetosphere creates a large-scale magnetospheric electrical convection field that is oriented from the morning side to the evening side. The maximum electrical potential difference is about 15 kV with low geomagnetic activity and significantly more with disturbed conditions. Such a field forces a charge separation on both sides of the magnetopause . An electrical discharge current flows on the morning side along the last open field lines of the earth's magnetic field into the aurora zones of the ionospheric dynamo layer, there in two narrow bands to the evening side and back to the evening side of the magnetopause. The current bands flowing in the dynamo layer are called DP1 currents or polar electric jets. Even in geomagnetically calm conditions, they can reach currents of several mega amperes . The resulting ohmic losses and thus Joule heating are comparable to the solar XUV radiation in medium and low latitudes and significantly greater in disturbed conditions. This heat source is responsible for the creation of strong thermosphere and ionospheric storms.

DP2 stream

A magnetospheric electric convection field drives a two-cell electric current system located on the morning and evening sides in the polar regions of the dynamo layer. It's called DP2 stream. This current system already exists under geomagnetically extremely calm conditions and is then called S q p . It essentially consists of Hall currents.

Polar ring current

When the earth is in an interplanetary magnetic field sector facing away from the sun, the magnetospheric plasma is slowed down in the north polar cap and accelerated in the south polar cap. In the opposite case, the north cap is accelerated and the south cap is braked. This deviation from the co-rotation disappears outside the polar caps. The magnetic effect on the ground corresponds to that of a polar Hall current, which circles the poles at a distance of approx. 10 ° pole spacing, clockwise for an observer on earth in the case of an interpolar sector structure that is directed away from the sun, counterclockwise Trap of a sector structure directed towards the sun.

literature

Further texts:

  • MC Kelly: The Earth 'Ionosphere: Plasma Physics and Electrodynamics . Akademic press, New York 2009.
  • G. Proelss and MK Bird: Physics of the Earth's Space Environment: An Introduction . Springer, Berlin 2010.
  • A. Brekke: Physics of the Upper Polar Atmosphere . Springer, Berlin 2013.

Individual evidence

  1. ↑ a b c d e S. J. Chapman, J. Bartels: Geomagnetism. Clarendon Press, 1951.
  2. ↑ a b S. I. Akasofu: Physics of Magnetospheric Substorms. Reidel, Dordrecht, 1977.
  3. ↑ JP Heppner, ER in Dyer (ed.): Critical Problems of Magnetospheric Physics. Nat. Acad. Sci., Washington, DC, 1972, p. 107.
  4. ^ Viggiano, AA, and F. Arnold, in Volland, H. (ed), "Handbook of Atmospheric Electrodynamics", Vol. 1, p. 1, CRC Press, Boca Raton, FL, 1995
  5. ^ Fejer, AA, Rev. Geophys., 2, 275, 1964
  6. ^ Longuet-Higgins, MS, "The Eigenfunctions of Laplace's tidal equations over a sphere," Phil. Trans. Roy. Soc. ", London, A262, p. 511, 1968
  7. ↑ a b Volland, H., "Atmospheric Tidal and Planetary Waves", Kluwer Publ., Dordrecht, 1988
  8. ↑ a b Chapman, S., and RS Lindzen, "Atmospheric Tides", Kluwer Dordrecht, 1970
  9. ↑ Kohl, H. and JW King, J. Atm. Terr. Phys., 29, 1045, 1967
  10. ↑ Fukushima, N., Radio Sci., 6, 269, 1971
  11. ↑ Malin, SRC, Phil Trans. R. Soc., London, Ser. A 274, 551, 1973
  12. ↑ Forbes, JM, at all., J. Geophys. Res., Space Physics, 113, 17, 2008
  13. ^ Matsushita, S., and WH Campell, WH (eds.), "Physics of Geomagnetic Phenomena", Vol. I and II, Academic Press, New York, 1967
  14. ↑ Kato, S., J. Geophys. Res., 71, 3211, 1966
  15. ↑ a b c Volland, H., "Atmospheric Electrodynamics", Kluwer, Dordrecht, 1984
  16. ↑ Forbes, JM, J. Geophys. Res. 87, 5222, 1988
  17. ↑ Richmond, A.DF., and SV Venkatesmaran, J. Geophys. Res., 81, 139, 1971
  18. ↑ Wagner, CU, J. Atm. Terr. Phys., 25,529,1963
  19. ↑ Blanc, M., and AD Richmond, J. Geophys. Res., 85, 1669, 1980
  20. ↑ Zaka, K, .Z., Et all., Ann. Geophys., 27, 3523, 2009
  21. ↑ Richmond, AD, Geomagn. and Geoelectr. 31, 287, 1979
  22. ↑ Gerd W. Prölss, in: H. Volland (ed.): Handbook of Atmospheric Electrodynamics. Vol. II, CRC Press, Boca Raton, FL, 1995, p.195
  23. ^ Gerd W. Prölss: Density Perturbations in the Upper Atmosphere Caused by the Dissipation of Solar Wind Energy . In: Surveys in Geophysics . tape 32 , no. 2 , December 3, 2010, p. 101-195 , doi : 10.1007 / s10712-010-9104-0 .
  24. ^ Nishida, A., and S. Kokubun, Rev. Geophys. Space Sci., 9, 417, 1971
  25. ↑ Svalgaard, L., J. Geophys. Res., 78, 2064, 1973