j function

j-function in the complex plane (without factor 12 ^ 3)

The j-function or absolute invariant plays an important role in the theory of elliptic functions and modular forms . It is a fundamental module function in the sense that all further module functions result from it through rational functions.

definition

For (upper half plane) is ${\displaystyle \tau \in \mathbb {H} :=\{z\in \mathbb {C} ;\Im (z)>0\}}$

${\displaystyle j(\tau ):=12^{3}\cdot {\frac {g_{2}^{3}(\tau )}{\Delta (\tau )}}}$,

where is the discriminant ; and are the rows of iron stones to the grid . ${\displaystyle \Delta (\tau ):=g_{2}^{3}(\tau )-27g_{3}^{2}(\tau )}$ ${\displaystyle g_{2}(\tau )=60G_{4}(\tau )}$ ${\displaystyle g_{3}(\tau )=140G_{6}(\tau )}$ ${\displaystyle \mathbb {Z} \tau +\mathbb {Z} }$

properties

Fundamental domain (blue) of the j-function

The j-function is holomorphic (it has only one single pole at the top, i.e. for ), the designation absolute invariant is explained by the transformation behavior among the substitutions of the module group , namely: ${\displaystyle \mathbb {H} }$ ${\displaystyle \Im (z)\to \infty }$ ${\displaystyle \Gamma :=SL_{2}(\mathbb {Z} )=\left\{{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\mid a,b,c,d\in \mathbb {Z} ,ad-bc=1\right\}}$

${\displaystyle j\left({\frac {a\tau +b}{c\tau +d}}\right)=j(\tau )}$, ie is a module function . ${\displaystyle j}$

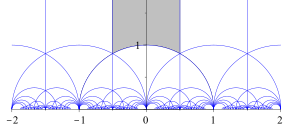
The j-function surjectively maps to . The following applies to points if and only if there is a complex number that the grid transfers to the grid , i.e. exactly when the quotients and are isomorphic as elliptic curves . So it clearly parameterizes the elliptic functions. It delivers a bijection . Its fundamental area is given by the module figure (see illustration). ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle z,w\in \mathbb {H} }$ ${\displaystyle j(z)=j(w)}$ ${\displaystyle a\in \mathbb {C} ^{*}}$ ${\displaystyle \mathbb {Z} +z\mathbb {Z} }$ ${\displaystyle \mathbb {Z} +w\mathbb {Z} }$ ${\displaystyle \mathbb {C} /(\mathbb {Z} +z\mathbb {Z} )}$ ${\displaystyle \mathbb {C} /(\mathbb {Z} +w\mathbb {Z} )}$ ${\displaystyle \mathbb {H} \backslash \Gamma \to \mathbb {C} }$

If an element consists of a square number field with a positive imaginary part, then is an integer algebraic number . ${\displaystyle \tau }$ ${\displaystyle j(\tau )}$

Every modular function is a rational function of the j-function.

Fourier expansion

The j-function can be expanded into a Fourier series :

${\displaystyle j(\tau )={\frac {1}{q}}+744+196884q+21493760q^{2}[phone]q^{3}+\ldots =\sum _{n=-1}^{\infty }c_{n}q^{n}}$

With ${\displaystyle q=\mathrm {e} ^{2\pi \mathrm {i} \tau }.}$

All Fourier coefficients : ${\displaystyle c_{n}}$

${\displaystyle 1,744,196884,21493760,\dots }$(Follow A000521 in OEIS )

are natural numbers . The asymptotic formula applies to their growth

${\displaystyle c_{n}\cong {\frac {e^{4\pi {\sqrt {n}}}}{{\sqrt {2}}n^{3/4}}}}$,

which was proven by Petersson in 1932 and independently thereof by Rademacher in 1938 .

The Fourier coefficients are linear combinations of the dimensions of the irreducible representations of the monster group with small integer coefficients. This follows from a deep mathematical relationship that was conjectured by McKay , Conway , Norton and proven by Richard Borcherds ("monstrous moonshine").

literature

• Eberhard Freitag & Rolf Busam: Function Theory 1 , 4th edition, Springer, Berlin (2006), ISBN 3-540-31764-3
• Max Koecher & Aloys Krieg : Elliptical functions and modular forms , 2nd edition, Springer, Berlin (2007) ISBN 978-3-540-49324-2

Web links

• Eric W. Weisstein : j-Function . In: MathWorld (English).
• Ramanujan and the Modular j -Invariant (PDF; 14 p., 143 kB)
• A. Scherer, The j-function and the Monster, pdf

References and comments

1. ↑ This follows from the fact that there are Eisenstein series in the numerator, which are holomorphic in this limiting case, and the discriminant, which is a peak shape and has a simple zero in the limiting case under consideration, in the denominator