Cable theory

Fig. 1: Schematic representation of the resistances and capacities on an axon .

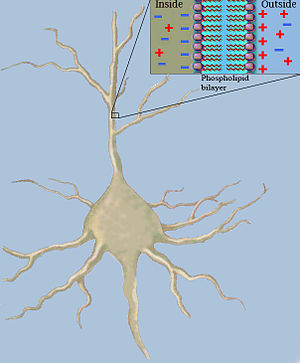
Classical cable theory tries to describe the electrical currents and the potential differences along passive nerve fibers ( neurites ), especially along dendrites , with the help of mathematical models. To simplify matters, the nerve fibers are viewed as a series of similarly structured cylindrical segments. The wall of each of these segments is formed by the lipid bilayer of the axon membrane, the electrical properties of which can be described as the parallel connection of an electrical resistance and a capacitor with capacitance . The capacity of the nerve fiber results from the electrostatic forces that are effective due to the unequal distribution of charge in the extra and intracellular space across the very thin lipid bilayer of the plasma membrane (see Fig. 2). In the longitudinal direction of the nerve fiber, the resistance that the cytosol opposes to the movement of electrically charged particles creates the longitudinal resistance . ${\displaystyle r_{m}}$ ${\displaystyle c_{m}}$ ${\displaystyle c_{m}}$ ${\displaystyle r_{l}}$

Fig. 2: Membrane capacity

history

The origins of cable theory date back to the 1850s when William Thomson (later known as Lord Kelvin) began developing mathematical models of the signal decay in submarine telegraphic cables. These models were similar to the partial differential equations used by Fourier to describe the conduction of heat in solids.

Around 1870 Hermann was the first to try to develop a model of the axonal electrotonus , based on the analogies to heat conduction. However, it was only JL Hoorweg who discovered the similarity to Kelvin's submarine cables in 1898. As a result, it was Hermann and Cremer who independently developed the cable theory for nerve fibers at the beginning of the 20th century. Further mathematical theories about the conduction of excitation in nerve fibers based on the cable theory have been published by Cole and Hodgkin (1920-1930), Offner et al. (1940) and Rushton elaborated.

Experimental evidence of the importance of cable theory in describing real nerve fibers was provided in the 1930s by work by Cole, Curtis, Hodgkin, Bernard Katz , Rushton, Tasaki, and others. Two important articles from this period are from Davis and Lorente de No, and Hodgkin and Rushton, respectively.

Due to the further development of the techniques for measuring electrical activity on individual nerve fibers in the 1950s, cable theory gained increasing importance in the analysis of currents and voltages derived intracellularly with microelectrodes as well as in the investigation of the electrical properties of neuronal dendrites. Scientists such as Coombs, Eccles , Fatt, Frank, Fuertos and others have now used cable theory to design new experiments to gain new insights into how neurons work.

Later on, cable theory, with its mathematical formulas, allowed increasingly sophisticated neuron models , which were studied by scientists such as Rall , Redman, Rinzel, Idan Segev, Tuckwell, Bell, Poznanski and Ianella.

Several important approaches to expanding cable theory have recently led to the use of ion channels and endogenous structures to investigate the effects of different distributions of synaptic input across the dendritic surface.

Derivation of the cable equation

The sizes introduced above and are measured as a function of the fiber length. Therefore the unit has [Ωm] and farad per meter ([F / m]). In contrast to this, the specific membrane resistance and the specific membrane capacity are measured as a function of the membrane surface and have the unit [Ω m ² ] or [F / m ² ]. If the fiber radius r, which is assumed to be constant for the sake of simplicity, is known and the fiber circumference accordingly , then and can be calculated as follows: ${\displaystyle r_{m}}$ ${\displaystyle c_{m}}$ ${\displaystyle r_{m}}$ ${\displaystyle c_{m}}$ ${\displaystyle R_{m}}$ ${\displaystyle C_{m}}$ ${\displaystyle 2\pi r\ }$ ${\displaystyle r_{m}}$ ${\displaystyle c_{m}}$

${\displaystyle r_{m}={\frac {R_{m}}{2\pi r\ }}}$   (1)

${\displaystyle c_{m}=C_{m}\,2\pi r\ }$   (2)

The equations can be understood if one realizes that the membrane surface is proportional to the fiber circumference: The membrane resistance decreases with increasing fiber circumference, because the charged particles now have a larger area available for passage. The membrane capacity increases accordingly because the surface of the capacitor formed by the plasma membrane increases due to the larger fiber circumference .

In a similar way, the specific resistance (unit: [Ωm]) of the cytoplasm allows the calculation of the intracellular longitudinal resistance of the fiber with the unit [Ω / m]: ${\displaystyle \rho _{l}}$ ${\displaystyle r_{l}}$

${\displaystyle r_{l}={\frac {\rho _{l}}{\pi r^{2}\ }}}$   (3)

In order to better understand the derivation of the cable equation, the nerve fiber described in the introduction is first simplified further: in the following it is assumed that it has a plasma membrane that is absolutely impermeable to charged particles, that is, that it is infinitely large and therefore no charge loss occurs to the outside. Let the membrane capacity also be zero ( ). A current which, under these assumptions, is  injected into the nerve fiber at position x = 0, would continue unchanged along the interior of the fiber. With increasing distance from the place of injection of the current, the change in voltage can be calculated with the help of Ohm's law: ${\displaystyle r_{m}}$ ${\displaystyle c_{m}=0}$

${\displaystyle \Delta V=-i_{l}\,r_{l}\,\Delta x\ }$   (4)

If Δ x is allowed to approach zero, the following partial differential equation is obtained :

${\displaystyle {\frac {\partial V}{\partial x}}=-i_{l}\,r_{l}\ }$   (5)

or

${\displaystyle {\frac {1}{r_{l}}}{\frac {\partial V}{\partial x}}=-i_{l}\ }$   (6)

If you now include the fact that it is not infinitely large again in the considerations, it is like making holes in a garden hose. The more holes the hose contains, the more water will be lost to the outside and the less water will reach a certain point on the hose. Similarly, in the nerve fiber, some of the longitudinal current through the plasma membrane will be lost. ${\displaystyle r_{m}}$

If the current is lost across the membrane per fiber section, then the sum of all currents lost along n sections is given by . The change in current in the cytoplasm after traveling the distance can therefore be written as ${\displaystyle i_{m}}$ ${\displaystyle n\cdot i_{m}}$ ${\displaystyle \Delta i}$ ${\displaystyle \Delta x}$

${\displaystyle \Delta i_{l}=-i_{m}\,\Delta x\ }$   (7)

or.

${\displaystyle {\frac {\partial i_{l}}{\partial x}}=-i_{m}\ }$  (8th)

Taking into account that the capacity is not zero, it can be expressed with the help of another formula. The capacitance creates a flow of charge in the cytoplasm in the direction of the membrane, which is usually referred to as displacement current and is written below as . This current will only flow as long as the membrane voltage has not reached its final value. can then be expressed as: ${\displaystyle c_{m}}$ ${\displaystyle i_{m}}$ ${\displaystyle c_{m}}$ ${\displaystyle i_{c}}$ ${\displaystyle i_{m}}$

${\displaystyle i_{c}=c_{m}\,{\frac {\partial V}{\partial t}}\ }$   (9)

where describes the change in potential as a function of time. The current that flows across the membrane is calculated according to Ohm's law as follows: ${\displaystyle {\partial V}/{\partial t}}$ ${\displaystyle i_{r}}$

${\displaystyle i_{r}={\frac {V}{r_{m}}}}$  (10)

Because further holds that , the result for : ${\displaystyle i_{m}=i_{r}+i_{c}}$ ${\displaystyle i_{m}}$

${\displaystyle {\frac {\partial i_{l}}{\partial x}}=-i_{m}=-({\frac {V}{r_{m}}}+c_{m}\,{\frac {\partial V}{\partial t}})}$   (11)

${\displaystyle {\partial i_{l}}/{\partial x}}$ indicates the change in the current flowing in the longitudinal direction per fiber section.

By inserting equation (6) into (11), we get the following partial differential equation of the second order as the first version of the cable equation:

${\displaystyle {\frac {1}{r_{l}}}{\frac {\partial ^{2}V}{\partial x^{2}}}=c_{m}\,{\frac {\partial V}{\partial t}}+{\frac {V}{r_{m}}}}$  (12)

By rearranging equation (12) (see below), two important quantities are obtained, namely the membrane longitudinal constant and the membrane time constant , which are described in more detail in the next sections. ${\displaystyle \lambda }$ ${\displaystyle \tau }$

Longitudinal membrane constant

The membrane longitudinal constant with the unit is a parameter that indicates how far a current will propagate along the inside of the nerve fiber and thus influence the tension along this route. The larger , the further the current spreads. The longitudinal constant is calculated from the membrane resistance and the longitudinal resistance as follows: ${\displaystyle \lambda }$ ${\displaystyle m}$ ${\displaystyle \lambda }$ ${\displaystyle r_{m}}$ ${\displaystyle r_{l}}$

${\displaystyle \lambda ={\sqrt {\frac {r_{m}}{r_{l}}}}}$   (13)

The greater the membrane resistance , the more current remains in the cytosol in order to travel along the nerve fiber, which leads to an increase in the membrane longitudinal constant. The same applies to a reduction in the longitudinal resistance , because it is now easier for the charge carriers to move along the nerve fiber. Solving equation (12), one arrives at the following equation, which is valid for a stable state, for example when the time t approaches infinity: ${\displaystyle r_{m}}$ ${\displaystyle r_{l}}$

${\displaystyle V_{x}=V_{0}\,e^{-{\frac {x}{\lambda }}}}$   (14)

${\displaystyle V_{0}}$is the potential difference across the plasma membrane at the point (location of the current injection), "e" is Euler's number and the potential difference at the distance "x" from the location of the current injection. Is , then: ${\displaystyle x=0}$ ${\displaystyle V_{x}}$ ${\displaystyle x=\lambda }$

${\displaystyle {\frac {x}{\lambda }}=1}$   (15)

and

${\displaystyle V_{x}={\frac {V_{0}}{e}}}$   (16)

If the potential difference is measured at the distance from , one obtains ${\displaystyle V}$ ${\displaystyle x=\lambda }$ ${\displaystyle x=0}$

${\displaystyle V_{\lambda }={\frac {V_{0}}{e}}=0,368\,V_{0}}$  (17)

It follows that there is always 36.8 percent of . The membrane longitudinal constant therefore specifies the exact distance in meters at which the potential difference has dropped to 36.8 percent . ${\displaystyle V_{\lambda }}$ ${\displaystyle V_{0}}$ ${\displaystyle V_{0}}$

Membrane time constant

Neurobiologists are often interested in how quickly the membrane potential of a nerve fiber changes in response to a change in the current injected into the cytosol. This speed is described with the help of the so-called. "Membrane time constant" , which indicates the time in seconds after which the amplitude of the potential difference has decreased to 36.8% of the initial value. The membrane time constant is therefore a direct measure of the speed of the change in potential, which can be calculated as follows: ${\displaystyle V_{m}}$ ${\displaystyle \tau }$

${\displaystyle \tau =r_{m}\cdot c_{m}\ }$   (18)

Cable equation with membrane length and time constant

Multiplying equation (12) by on both sides gives: ${\displaystyle r_{m}}$

${\displaystyle {\frac {r_{m}}{r_{l}}}{\frac {\partial ^{2}V}{\partial x^{2}}}=c_{m}\,r_{m}\,{\frac {\partial V}{\partial t}}+V}$   (19)

If you replace through and through , you get what is perhaps the best-known form of the cable equation: ${\displaystyle {\frac {r_{m}}{r_{l}}}}$ ${\displaystyle \lambda ^{2}}$ ${\displaystyle r_{m}\cdot c_{m}}$ ${\displaystyle \tau }$

${\displaystyle \lambda ^{2}\,{\frac {\partial ^{2}V}{\partial x^{2}}}=\tau \,{\frac {\partial V}{\partial t}}+V}$   (20)

Remarks

In the introduction it is mentioned that the cable theory describes the conditions of passive nerve fibers. In this case, passive means the independence of the membrane resistance from the membrane potential. Recent studies with dendritic membranes have shown, however, that many of them are equipped with voltage-dependent ion channels and that the membrane resistance therefore depends on the membrane potential. Consequently, an adaptation of the classical cable theory is necessary to take this fact into account. ${\displaystyle r_{m}}$

See also

• Excitation conduction
• Bioelectrochemistry

Individual evidence

1. ↑ JL Hoorweg; About the electrical properties of the nerves . Arch. J. d. total Physiology vol. 71 p. 141 u. 142,1898; quoted in: Pflüger's archive for the entire physiology of humans and animals . Vol. 133, Bonn 1910
2. ^ Lussier JJ, WAH Rushton: The relation between the space constant and conduction velocity in nerve fibers of the A group from the frog's sciatic . In: The Journal of Physiology . 114, July 1951, pp. 399-409. PMID 14861824 .
3. ^ WAH Rushton: A theory of the effects of fiber size in medullated nerve . In: The Journal of Physiology . 115, September 1951, pp. 101-122. PMID 14889433 .
4. ↑ DAVIS L Jr, LORENTE de NO R .: Contribution to the mathematical theory of the electrotonus . In: Rockefeller Institute for Medical Research . 131, 1947, pp. 442-496. PMID 20261883 .
5. ↑ AL Hodgkin, WAH Rushton: The electrical constants of a crustacean nerve fiber . In: Proceedings of the Royal Society of Medicine . 133, No. 873, December 1946, pp. 444-479. PMID 20281590 .
6. ^ Henry C. Tuckwell: Introduction to Theoretical Neurobiology . Cambridge University Press, 4 1988, ISBN 0521350964 .
7. ^ Roman R. Poznanski: Thermal noise due to surface-charge effects within the Debye layer of endogenous structures in dendrites . In: Physical Review . 81, No. 2, February 2010. PMID 20365590 .
8. ^ Greg J. Stuart, Bert Sakmann: Active propagation of somatic action potentials into neocortical pyramidal cell dendrites . In: Nature . 367, January 1994, pp. 69-72. PMID 8107777 .