Congruent number

This article deals with congruent numbers in terms of area. For congruence regarding division with remainder, see Congruence (number theory) .

Triangle with area 6, a congruent number.

In number theory , congruent numbers are whole numbers that can be represented as the area of a right triangle with rational side lengths. Historically, the eponymous are "meeting" (Latin congruere) arithmetic sequences of square numbers, which is based on congruum, pl. Introduced by Leonardo Fibonacci . congrua , which multiplied by a suitable rational square form the congruent numbers . Édouard_Lucas proved in 1877 for congruent numbers n the context of rational solutions to the equation . ${\displaystyle y^{2}=x^{4}-n^{2}}$Kurt Heegner was the first to combine the problem of congruent numbers with elliptic curves , and in 1952 he proved that a prime number is a congruent number if or . ${\displaystyle p=5\mod 8}$ ${\displaystyle p=7\mod 8}$

The sequence of congruent numbers (sequence A003273 in OEIS ) begins with

5, 6, 7, 13, 14, 15, 20, 21, 22, 23, 24, 28, 29, 30, 31, 34, 37, 38, 39, 41, 45, 46, 47, ...

Table of congruent numbers: n ≤ 120
-: Non-congruent number K: Square-free congruent number Q: Congruent number with a quadratic factor
n	1	2	3	4th	5	6th	7th	8th
	-	-	-	-	K	K	K	-
n	9	10	11	12	13	14th	15th	16
	-	-	-	-	K	K	K	-
n	17th	18th	19th	20th	21st	22nd	23	24
	-	-	-	Q	K	K	K	Q
n	25th	26th	27	28	29	30th	31	32
	-	-	-	Q	K	K	K	-
n	33	34	35	36	37	38	39	40
	-	K	-	-	K	K	K	-
n	41	42	43	44	45	46	47	48
	K	-	-	-	Q	K	K	-
n	49	50	51	52	53	54	55	56
	-	-	-	Q	K	Q	K	Q
n	57	58	59	60	61	62	63	64
	-	-	-	Q	K	K	Q	-
n	65	66	67	68	69	70	71	72
	K	-	-	-	K	K	K	-
n	73	74	75	76	77	78	79	80
	-	-	-	-	K	K	K	Q
n	81	82	83	84	85	86	87	88
	-	-	-	Q	K	K	K	Q
n	89	90	91	92	93	94	95	96
	-	-	-	Q	K	K	K	Q
n	97	98	99	100	101	102	103	104
	-	-	-	-	K	K	K	-
n	105	106	107	108	109	110	111	112
	-	-	-	-	K	K	K	Q
n	113	114	115	116	117	118	119	120
	-	-	-	Q	Q	K	K	Q

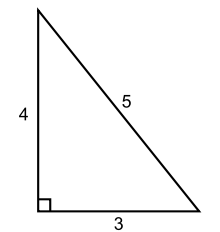
Example: The whole number 6 is a congruent number, because the right-angled triangle with the cathets and has the area and, according to the Pythagorean theorem, the hypotenuse . So the whole number 6 as the area of ​​a right triangle with rational side lengths is a congruent number. ${\displaystyle a=3}$ ${\displaystyle b=4}$ ${\displaystyle A={\tfrac {1}{2}}ab=6}$ ${\displaystyle c={\sqrt {a^{2}+b^{2}}}={\sqrt {9+16}}=5}$

For any positive integer , an integer is a congruence number if and only if is a congruence number. Therefore one can restrict oneself to square-free numbers when solving the congruence number problem . ${\displaystyle s}$ ${\displaystyle q}$ ${\displaystyle s^{2}q}$

More generally, all rational numbers that appear as the area of ​​a right triangle with rational side lengths are also called congruent numbers.

Congruent numbers in the range 1 to 20

The following integers in the range 1 to 20 are congruent because they are the area of a right triangle with rational short sides and and rational hypotenuse can be displayed: ${\displaystyle A={\tfrac {1}{2}}ab}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c={\sqrt {a^{2}+b^{2}}}}$

Right triangle with the hypotenuse c and the legs a and b.

Area ${\displaystyle A}$	Cathete ${\displaystyle a}$	Cathete ${\displaystyle b}$	hypotenuse ${\displaystyle c}$
${\displaystyle 5}$	${\displaystyle {\tfrac {3}{2}}}$	${\displaystyle {\tfrac {20}{3}}}$	${\displaystyle {\tfrac {41}{6}}}$
${\displaystyle 6}$	${\displaystyle 3}$	${\displaystyle 4}$	${\displaystyle 5}$
${\displaystyle 7}$	${\displaystyle {\tfrac {35}{12}}}$	${\displaystyle {\tfrac {24}{5}}}$	${\displaystyle {\tfrac {337}{60}}}$
${\displaystyle 13}$	${\displaystyle {\tfrac {780}{323}}}$	${\displaystyle {\tfrac {323}{30}}}$	${\displaystyle {\tfrac {106921}{9690}}}$
${\displaystyle 14}$	${\displaystyle {\tfrac {8}{3}}}$	${\displaystyle {\tfrac {63}{6}}}$	${\displaystyle {\tfrac {65}{6}}}$
${\displaystyle 15}$	${\displaystyle 4}$	${\displaystyle {\tfrac {15}{2}}}$	${\displaystyle {\tfrac {17}{2}}}$
${\displaystyle 20}$	${\displaystyle 3}$	${\displaystyle {\tfrac {40}{3}}}$	${\displaystyle {\tfrac {41}{3}}}$

Fermat's theorem

The French mathematician Pierre de Fermat proved that the area of ​​a right triangle with integral sides cannot be a square number . This is equivalent to saying that neither 1 nor any other square number is a congruent number. He communicated his result in a letter to Pierre de Carcavi in 1659 , and noted the evidence in a note that was published posthumously in 1670. Fermat starts from the representation of a primitive Pythagorean triple known since antiquity as ( x ² - y ² , 2 xy , x ² + y ² ) and uses the method of infinite descent he introduced , a variant of complete induction . His proof also shows that the equation a ⁴ + b ⁴ = c ^{4 has} no solution with positive integers a , b , c (a special case of Fermat's conjecture ).

Tunnell's theorem

Tunnell's Theorem, named after Jerrold B. Tunnell , gives necessary conditions for a number to be congruent.

For a square-free integer, define ${\displaystyle n}$

${\displaystyle {\begin{aligned}A_{n}&=\#\{x,y,z\in \mathbb {Z} \mid n=2x^{2}+y^{2}+32z^{2}\},\\B_{n}&=\#\{x,y,z\in \mathbb {Z} \mid n=2x^{2}+y^{2}+8z^{2}\},\\C_{n}&=\#\{x,y,z\in \mathbb {Z} \mid n=8x^{2}+2y^{2}+64z^{2}\},\\D_{n}&=\#\{x,y,z\in \mathbb {Z} \mid n=8x^{2}+2y^{2}+16z^{2}\}.\end{aligned}}}$

If is an odd congruence number then must be, if is an even congruence number then must be. ${\displaystyle n}$ ${\displaystyle 2A_{n}=B_{n}}$ ${\displaystyle n}$ ${\displaystyle 2C_{n}=D_{n}}$

If Birch and Swinnerton-Dyer's conjecture holds for elliptic curves of the form , then these conditions are also sufficient. Then the natural number n would be congruent if and only if the Abelian group of the rational points of the elliptic curve has a rank at least 1. ${\displaystyle y^{2}=x^{3}-n^{2}x}$ ${\displaystyle E_{n}:y^{2}=x^{3}-n^{2}x}$

Pan Yan proved this conditionally in 2014 (weak form of the Birch and Swinnerton-Dyer conjecture) for all positive square-free integers . Continuing these ideas, Alexander Smith showed in 2016 that at least 55.9 percent of positive square-free integers are congruent numbers. ${\displaystyle n=5,6,7\mod 8}$ ${\displaystyle n=5,6,7\mod 8}$

literature

• Leonard Eugene Dickson : Congruent numbers in History of the theory of numbers. Volume II: Diophantine equations , Carnegie Institution, Washington 1920, pp. 459–472 (English)
• JB Tunnell : A classical Diophantine problem and modular forms of weight 3/2 , Inventiones mathematicae 72 (2), 1983, pp. 323–334 (English)

Individual evidence

1. ↑ Follow A003273 in OEIS
2. ↑ Neal Koblitz : Introduction to elliptic curves and modular forms , Springer-Verlag, 1984, 2nd edition 1993, ISBN 3-540-97966-2 , p. 3 (English)
3. ↑ Congruent numbers: Thousand-year-old geometry puzzle , Spiegel Online, January 31, 2013
4. ^ Paul Tannery , Charles Henry (ed.): Œuvres de Fermat. Tome deuxième , Gauthier-Villars, Paris 1894, pp. 431–436 (French)
5. ↑ Samuel de Fermat (Ed.): Diophanti Alexandrini Arithmeticorum libri sex, et de numeris multangulis liber unus , Bernard Bosc, Toulouse 1670, pp. 338f. ; also in Paul Tannery , Charles Henry (ed.): Œuvres de Fermat. Tome premier , Gauthier-Villars, Paris 1891, pp. 340f. (Latin)
6. ↑ Catherine Goldstein : Un théorème de Fermat et ses lecteurs , Presse Universitaire de Vincennes, St. Denis 1995, ISBN 2-910381-10-2 (French; table of contents , PDF file, 29.4 kB; review , Zentralblatt review )
7. ^ HG Zeuthen : History of Mathematics in the XVI. and XVII. Century , BG Teubner, Leipzig 1903, p. 163f.
8. ^ Pan Yan, Congruent Numbers and Elliptic Curves , math.okstate.edu
9. ^ Smith, The congruent numbers have positive natural density , Arxiv 2016

Web links

• Holger Dambeck: Mathematics: Solution for riddles from 1001 nights is getting closer. Spiegel Online , January 31, 2013, accessed February 1, 2013 .