Consistent estimation sequence

${\displaystyle \{T_{1},T_{2},\ldots \}}$is a sequence of estimators for the true parameter . This estimation sequence is consistent, since the probability distribution of the estimator concentrates more and more around the true (unknown) parameter as the sample size increases . However, these estimates are biased because they do not hit the true parameter on average. At , the probability distribution of at collapses . The asymptotic distribution of this estimation sequence is therefore a degenerate random variable that assumes the value with probability . ${\displaystyle \theta =4}$ ${\displaystyle n}$ ${\displaystyle \theta }$ ${\displaystyle n\to \infty }$ ${\displaystyle {\hat {\theta }}_{n}}$ ${\displaystyle \theta }$ ${\displaystyle \theta }$ ${\displaystyle 1}$

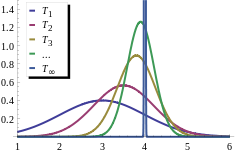
In estimation theory , a branch of mathematical statistics , a consistent estimation sequence is a sequence of point estimators , which is characterized by the fact that it estimates the value to be estimated more and more precisely as the sample size increases.

Depending on the type of convergence, a distinction is made between weak consistency ( convergence in probability ), strong consistency ( almost certain convergence ) and consistency ( convergence in the p-th mean ) with the special case of consistency in the square mean ( convergence in the square mean , special case of convergence in the p- th funds for ). If consistency is spoken of without an additive, the weak consistency is usually meant. Alternatively, the terms consistent sequence of estimators and consistent estimators can also be found, the latter being technically incorrect. As a result, however, the construction is mostly only due to the fact that the larger sample has to be formalized. The idea on which the episode is based mostly remains unchanged. ${\displaystyle L^{p}}$ ${\displaystyle p=2}$

The concept of consistency can also be formulated for statistical tests , in which case one speaks of consistent test sequences .

definition

Framework

A statistical model is given

${\displaystyle (X^{\mathbb {N} },{\mathcal {A}}^{\mathbb {N} },(P_{\vartheta }^{\mathbb {N} })_{\vartheta \in \Theta })}$

and a sequence of point estimates in an event space ${\displaystyle (T_{n})_{n\in \mathbb {N} }}$ ${\displaystyle (E,{\mathcal {E}})}$

${\displaystyle T_{n}\colon (X^{n},{\mathcal {A}}^{n})\to (E,{\mathcal {E}})}$,

which only depend on the first observations. Be ${\displaystyle n}$

${\displaystyle \tau \colon \Theta \to E}$

a function to be appreciated.

Consistency or weak consistency

The sequence is called a weakly consistent estimation sequence, or simply a consistent estimation sequence if it converges in probability to for each . So it applies ${\displaystyle (T_{n})_{n\in \mathbb {N} }}$ ${\displaystyle \vartheta \in \Theta }$ ${\displaystyle \tau (\vartheta )}$

${\displaystyle \lim _{n\to \infty }P_{\vartheta }(|T_{n}-\tau (\vartheta )|\geq \epsilon )=0}$

for everyone and everyone . Regardless of which of the probability measures is actually present, the probability that the estimated value is very close to the value to be estimated is 1 for randomly large samples. ${\displaystyle \epsilon >0}$ ${\displaystyle \vartheta \in \Theta }$ ${\displaystyle P_{\vartheta }}$

More consistency terms

The other consistency terms differ from the weak consistency term above only with regard to the type of convergence used. That's the name of the episode ${\displaystyle (T_{n})_{n\in \mathbb {N} }}$

• highly consistent when it almost certainly converges against for all ; ${\displaystyle P_{\vartheta }}$ ${\displaystyle \tau (\vartheta )}$
• consistent in the p-th mean if it converges against for all in the p-th mean ; ${\displaystyle P_{\vartheta }}$ ${\displaystyle \tau (\vartheta )}$
• consistent in the root mean square if it is consistent for in the pth mean. ${\displaystyle p=2}$

Detailed descriptions of the types of convergence can be found in the relevant main articles.

properties

Due to the properties of the types of convergence, the following applies: Both the strong consistency and the consistency in the p-th mean result in the weak consistency; all other implications are generally wrong.

Important tools for showing strong and weak consistency are the strong law of large numbers and the weak law of large numbers .

example

It can be shown that the least squares estimator obtained by the least squares method is consistent for , i.e. i.e., applies to him ${\displaystyle {\hat {\boldsymbol {\beta }}}=(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y} }$ ${\displaystyle {\boldsymbol {\beta }}}$

${\displaystyle {\hat {\boldsymbol {\beta }}}\;{\stackrel {p}{\longrightarrow }}\;{\boldsymbol {\beta }}}$or . ${\displaystyle \operatorname {plim} ({\hat {\boldsymbol {\beta }}})={\boldsymbol {\beta }}}$

The basic assumption to ensure the consistency of the KQ estimator is

${\displaystyle \lim _{T\to \infty }\left({\frac {\mathbf {X} _{T}^{\top }\mathbf {X} _{T}}{T}}\right)=\mathbf {Q} }$,

d. H. it is assumed that the average square of the observed values ​​of the explanatory variables remains finite even with an infinite sample size (see product sum matrix # asymptotic results ). It is also believed that

${\displaystyle \operatorname {plim} \left({\frac {\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }}}{T}}\right)=0}$.

The consistency can be shown as follows:

${\displaystyle {\begin{aligned}\operatorname {plim} (\mathbf {b} )&=\operatorname {plim} ((\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y} )\\&=\operatorname {plim} ({\boldsymbol {\beta }}+(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }}))\\&={\boldsymbol {\beta }}+\operatorname {plim} ((\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }})\\&={\boldsymbol {\beta }}+\operatorname {plim} \left(((\mathbf {X} ^{\top }\mathbf {X} )^{-1}/T)\right)\cdot \operatorname {plim} \left(((\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }})/T)\right)\\&={\boldsymbol {\beta }}+[\operatorname {plim} \left(((\mathbf {X} ^{\top }\mathbf {X} )/T)\right)]^{-1}\cdot \underbrace {\operatorname {plim} \left(((\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }})/T)\right)} _{=0}={\boldsymbol {\beta }}+\mathbf {Q} ^{-1}\cdot 0={\boldsymbol {\beta }}\end{aligned}}}$.

The Slutsky theorem and the property that when it is deterministic or non-stochastic applies. ${\displaystyle \mathbf {X} }$ ${\displaystyle \operatorname {plim} \left((\mathbf {X} ^{\top }\mathbf {X} )/T\right)=\lim \left((\mathbf {X} ^{\top }\mathbf {X} )/T\right)}$

Web links

• MS Nikulin: Consistent estimator . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).

literature

• Hans-Otto Georgii: Stochastics . Introduction to probability theory and statistics. 4th edition. Walter de Gruyter, Berlin 2009, ISBN 978-3-11-021526-7 , doi : 10.1515 / 9783110215274 .
• Ludger Rüschendorf: Mathematical Statistics . Springer Verlag, Berlin / Heidelberg 2014, ISBN 978-3-642-41996-6 , doi : 10.1007 / 978-3-642-41997-3 .
• Claudia Czado, Thorsten Schmidt: Mathematical Statistics . Springer-Verlag, Berlin / Heidelberg 2011, ISBN 978-3-642-17260-1 , doi : 10.1007 / 978-3-642-17261-8 .

Individual evidence

1. ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, TC Lee. Introduction to the Theory and Practice of Econometrics. John Wiley & Sons, New York, Chichester, Brisbane, Toronto, Singapore, ISBN 978-0471624141 , second edition 1988, p. 266.