Lab color space

Area	Colorimetry
title	Colorimetry - Part 4: CIE 1976 L * a * b * color space
Brief description:	CIELAB color space
Latest edition	2011-07
ISO	-

The Lab color space from above (view along the L axis). The spectral colors, i.e. H. Colors of maximum intensity in one or more wavelength ranges form its outer shell.

The L * a * b * color space (also: CIE LAB , CIEL * a * b * , Lab colors ) describes all perceptible colors . It uses a three-dimensional color space in which the brightness value L * is perpendicular to the color plane (a *, b *).

In analogy to Ewald Hering's counter-color theory, the a-coordinate indicates the color type and color intensity between green and red and the b-coordinate the color type and color intensity between blue and yellow. The larger the positive a and b values and the smaller the negative a and b values, the more intense the color. If a = 0 and b = 0, there is an achromatic hue on the lightness axis. In the usual software implementations, L (lightness) can assume values between 0 and 100 and a and b can be varied between −128 and 127. In the usual 8-bit model per color channel, 16.7 million possible Lab coordinates are achieved in this way. The real Lab color space (our color perception) goes in some areas beyond the mentioned a / b limits and does not reach the mentioned a / b limits in most areas.

The most important properties of the L * a * b * color model include device independence and perception-relatedness, i.e. colors are defined as they are perceived by a normal observer under standard lighting conditions, regardless of how they are generated or how they are reproduced .

The color model is standardized in EN ISO 11664-4 "Colorimetry - Part 4: CIE 1976 L * a * b * Color space". In Germany, this replaces DIN 6174, which was withdrawn in 2011, “Colorimetric determination of color dimensions and color differences in an approximately uniform CIELAB color space”.

Basics

CIE XYZ color space

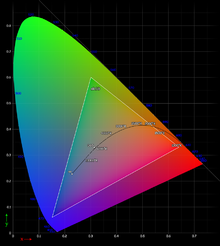
The CIELAB color system is based on the CIE-XYZ model of 1931, which combines the three spectral properties (intensity curves in the wavelength range 380-760 nm) of the type of light, the standardized normal observer and the remission properties of the color sample to form the "color valences" (XYZ ) offset against each other. These color valences describe the strength of the intensity of the stimulation of the three color receptor types with the values X, Y and Z. The graphic representation of the tristimulus model of the CIE is also known as the “CIE shoe sole”. It was widely used but was found to be impractical for evaluating color differences.

Hunter Lab color space

The color space, which was defined by Richard Sewall Hunter in 1948, is a color space that is also referred to as "Lab". Like CIELAB, it was designed so that color values can be transferred from the CIEXYZ space with simple formulas, but are more uniform in terms of perception than XYZ. Hunter named his coordinates L , a and b . The 1976 CIELAB color space coordinates have been labeled L * , a * and b * to distinguish them from the Hunter coordinates.

The CIELAB color wheel (360 °) shows the ring of highest CMYK chromacity. The color angle increases counterclockwise by ΔHue = 10.

CIELAB color space

In the color model of the International Commission on Illumination , the CIELAB model from 1976, the XYZ coordinates are subjected to a computational transformation in order to normalize areas of similar color differences around each color space coordinate to form circles. The so-called MacAdam ellipses , as areas of equally strong perceived color contrasts in the XYZ space, were irregularly shaped. With this, the Euclidean distances of equivalent differences in color perception should also be represented mathematically better.

Due to the desired equidistance, CIELAB describes our color perception better than the tristimulus model (CIE-XYZ). Due to the inclusion of the perceptual component (the normal observer), it describes the color perception better than RGB , CMYK , HSB or other popular mathematical color models. In contrast to these, it describes all colors, not just the color space segments ( gamuts ) that can be represented in a certain technique . As a mathematical color model, CIELAB is in the public domain and freely usable in every respect.

Coordinate system of the color space

CIELAB color space from the blue side (color angle H = 270). Above is the lightness peak with L = 100, below in the shadow is the color wheel scale.

Each color in the color space is defined by a color location with the Cartesian coordinates {L *, a *, b *}. The a * b * coordinate plane was constructed using the theory of opposing colors . On the a * axis, green and red are opposite, the b * axis runs between blue and yellow. Complementary color tones face each other by 180 °, in their middle (the origin of coordinates a * = 0, b * = 0) is gray.

The L * axis describes the brightness (luminance) of the color with values from 0 to 100. In the representation, this is perpendicular to the a * b * plane at the zero point. It can also be referred to as the neutral gray axis, because all achromatic colors (gray tones) are contained between the end points black (L * = 0) and white (L * = 100). The a * axis describes the green or red component of a color, with negative values for green and positive values for red. The b * axis describes the blue or yellow component of a color, with negative values standing for blue and positive values for yellow.

The a * values range from approx. −170 to +100, the b * values from −100 to +150, whereby the maximum values are only achieved with medium brightness of certain color tones. The CIELAB color body has its greatest expansion in the middle brightness range, but this is different in height and size depending on the color range. Overall, the CIELAB color body is very uneven - see figures.

Importance and improvements

The CIELAB color model found worldwide distribution in all areas of industrial color practice. Color measuring devices usually show L * a * b * color values, in common design programs (Adobe CC, Corel GS, GIMP and others) you can enter CIELAB color values directly, color differences are usually expressed as the Euclidean distance of the L * a * b * values two colors calculated and communicated ( ΔE ).

In the course of time, the CIE has developed further improved color difference formulas, which better take into account the dependence of a color difference on the color location and the viewing conditions (ΔE 94, ΔE CMC, ΔE 2000). These further arithmetic operations on the L * a * b * color values can be understood as a further distortion of the CIELAB body, which thus describes our color perception even better.

CIELAB as a neutral color instance

In order to avoid color shifts, the original image (left) was converted to Lab mode and the corrections (right) took place exclusively in the L channel.

The L * a * b * color space contains all colors in a device-independent form. It therefore allows the lossless conversion of color information from one color system to another, from one type of device to another.

Image processing software such as Adobe Photoshop use L * a * b * as the reference color system for conversion. Using so-called ICC profiles , in which a table with an L * a * b * target / actual comparison of defined colors is stored, the output of image files can be adapted from one color space to another or from one output device to another. So z. B. prepare image files created in sRGB for a specific RGB monitor and printer or convert them into the CMYK system required for printing, for example as "FOGRA 39" for offset printing.

L * a * b * coordinates are used as an exchange format between different devices.
L * a * b * is the internal color model of PostScript Level II.

Advantages and disadvantages

The CIELAB model offers strong advantages over other mathematical systems or systems that are firmly defined by the manufacturer.

Free calculability: The mathematical definition enables the free, stepless calculation of color and conversion into other color spaces.
Clear communication: information such as “Lab 20 30 40” or “HLC 240 40 22” are unambiguous worldwide. They can be made visible on any computer. In contrast to this, for information such as sky blue, defining original samples are always required.
Perception-relatedness: Due to the desired visual-computational equidistance, CIELAB describes our color perception better than the tristimulus model (CIE-XYZ). Due to the inclusion of the perceptual component (the normal observer), it describes the color perception better than RGB, HSB, CMYK or other common mathematical color models.
All colors: In contrast to other models, CIELAB clearly defines all colors, even those outside the gamuts of output processes. Color conversions in CIELAB are lossless.
no commercial interest: The CIE as a non-profit scientific association primarily pursues quality interests.
Copyright and license-free: As a mathematically defined color model, CIELAB is in the public domain, i. H. freely usable and integratable in every respect (also systematic Lab / HLC color value tables).
Worldwide distribution: The model is now a worldwide standard for color measurement and is integrated into the color selection of some design programs (Adobe Creative Cloud, Corel, GIMP, etc.).

Disadvantages of the model indicate a need for improvement.

Thin database: The definition of the MacAdam ellipses, the theoretical background of the aspired equidistance, was made on the basis of a small number of (individual) test persons and is not statistically significant.
No binding color samples: There are currently no systematic, gap-free CIELAB color samples whose accuracy meets the requirements of the industry.
Difficult to understand (Lab): Even experienced users find it difficult to imagine a specification such as “Lab 20 30 40” as a specific color. (The CIELAB polar coordinates HLC, on the other hand, are easier to understand: Quick color selection according to "Hue-Brightness-Saturation".)
Confusing color space. Depending on the color range, the characteristics in brightness and chromacity are very different. In contrast to simple geometric models, the color space cannot be grasped intuitively in its entirety (this also reflects the non-uniformity of our perception).
Gaps in software integration: The Lab color selection is not implemented in numerous software, confusingly, non-colors can always be generated and the easily understandable LCh / HLC color values can only be entered in a few niche products.

Coordinate transformation

Color valences XYZ

CIE shoe sole with the sRGB gamut it contains

According to Rösch (1928) , the CIE-XYZ color space is a three-dimensional space in which ever smaller horseshoe-shaped structures taper upwards towards the white point. In order to avoid the three-dimensionality of the display, which was not very practical at the time, a simple solution was found for the graphic display: The entire color impression is always set to 100%, regardless of whether the color is light, dark or highly saturated. The individual standard color values (xyz) can then be specified as a proportion of the total color (color valence). This means that all colors can be accommodated in a two-dimensional xy diagram (since z = 1-xy), referred to as a “standard color table” or known as the “CIE shoe sole” (English “horseshoe”). This includes all colors, but the representation of the "shoe sole" is always limited to the respective color-technical possibilities of the output process, the " gamut ". It should therefore be noted that the area outside of the sRGB triangle is not shown saturated enough in the adjacent illustration of the “shoe sole”.

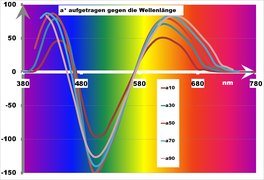
The outer upper curve of the shoe sole represents the spectral colors, which represent the maximum achievable color intensities. They have maximum light in a single wavelength interval and no light in the others. In the lower straight connection, the “purple straight”, maximum intensities of the beginning and end of the spectrum coincide. The close relationship of the spectral color sequence to the CIEL * a * b * color circle can be seen.

Representation L *, a *, b * depending on the wavelength
Luminance L *
Green-red parameter a *
Blue-yellow parameter b *
Diagram of the a * / b * plane.

The XYZ color space is not perceptually equally spaced. The numerically equal color difference between two color words is not perceived as a color difference of the same type in the entire color body. Therefore, the XYZ color space is unsuitable as a universal metric , analogous to the meter measure from the length range. For the L * a * b * color model, the XYZ color space is distorted perceptually using mathematical transformations in order to overcome this disadvantage.

Conversion from XYZ to Lab

Depending on the observer angle and type of light, different standard valences must be taken into account in the calculation. The observer angle of 2 ° corresponds to the CIE standard observer from 1931, the angle of 10 ° corresponds to the CIE standard observer from 1976. The 2 ° results from the area of the best color vision in the eye, 10 ° are the viewing angle of an A4 sheet of paper (usual) viewing distance. In America, the light type D50 = 5000K is preferred (direct solar radiation), in Europe the standard light type D65 = 6500K (covered sky when sampling at the north window). The following are the respective X _n Y _n Z _n values which must be entered in the calculation formulas.

Light type	X _{n (2 °)}	Y _{n (2 °)}	Z _{n (2 °)}	X _{n (10 °)}	Y _{n (10 °)}	Z _{n (10 °)}
D50	96,422	100	82,521	96.720	100	81,427
D65	95,047	100	108.883	94.811	100	107,304

brightness: ${\ displaystyle L ^ {*} = 116 \ cdot {\ sqrt [{3}] {\ frac {Y} {Y_ {n}}}} - 16}$
Green − red: ${\ displaystyle a ^ {*} = 500 \ cdot \ left ({\ sqrt [{3}] {\ frac {X} {X_ {n}}}} - {\ sqrt [{3}] {\ frac { Y} {Y_ {n}}}} \; \ right)}$
Yellow − blue: ${\ displaystyle b ^ {*} = 200 \ cdot \ left ({\ sqrt [{3}] {\ frac {Y} {Y_ {n}}}} - {\ sqrt [{3}] {\ frac { Z} {Z_ {n}}}} \; \ right)}$

The factors 500 and 200 should bring the resulting values for a * and b * into the usual order of magnitude, which also fits the maximum L * of 100.

For small values: ${\ displaystyle {\ frac {P} {P_ {n}}} <{\ frac {216} {24389}} \ approx 0 {,} 008 \, 856}$

the third root is replaced by the following relationship:

{\ displaystyle {\ frac {1} {116}} \ cdot \ left ({\ frac {24389} {27}} \ cdot {\ frac {P} {P_ {n}}} + 16 \ right)}

where P stands for X, Y, Z.

Conversion from Lab to HLC

View from above onto the a * / b * plane: A CIELAB color in Cartesian L * a * b * or HLC polar coordinates

The LCh color space with the coordinates (L * C * h °) corresponds to the Lab color space in which the Cartesian coordinates a * and b * are polar coordinates C * (distance from the origin) and h ° (angle to the a-axis) can be specified. This makes the CIELAB coordinates clearer: h ° can be interpreted as the basic color (hue) and C * as its intensity (chroma, chromacity).

The notation HLC is used for the polar representation , in which the usual order of color selection (hue H - lightness L - saturation C) is expressed. Other alternative abbreviations are LCh or LCH .

From L * a * b *, hue h ° and chromaticity C * can be calculated as follows:

Color (hue)

${\ displaystyle h_ {ab} ^ {o} = \ arctan \ left ({\ frac {b ^ {*}} {a ^ {*}}} \ \ right)}$

Brightness (luminance)

${\ displaystyle L_ {Lab} ^ {*} = L_ {LCh} ^ {*}}$

Colourfulness (chroma)

${\ displaystyle C_ {ab} ^ {*} = {\ sqrt {(a ^ {*}) ^ {2} + (b ^ {*}) ^ {2}}}}$

The HSB / HSL room used in numerous computer programs differs fundamentally from the HLC room. Although it is also interpreted as “hue, saturation, brightness”, it is less perceptual due to the conversion of the technically based RGB definition .

Conversion from RGB to Lab

Color spaces are complex mathematical bodies and the conversion is system-related accordingly. The RGB color space is always device-specific and Lab is perception-oriented. In addition, the L * a * b * color space comprises a larger color range than any (technically comprehensible) RGB color space. In the case of Lab RGB calculations, it must be clarified how the colors that are outside the (RGB) target color space are projected into them ( gamut mapping ).

A transformation of the present RGB color space into the L * a * b * color space is carried out via the CIE 1931 color space (XYZ coordinates), whereby device independence is initially achieved. As an example, the conversion formulas from sRGB to XYZ follow.

{\ displaystyle {\ begin {aligned} X & \, = \, 0 {,} 4124564 \ cdot R \, + \, 0 {,} 3575761 \ cdot G \, + \, 0 {,} 1804375 \ cdot B \ \ Y & \, = \, 0 {,} 2126729 \ cdot R \, + \, 0 {,} 7151522 \ cdot G \, + \, 0 {,} 0721750 \ cdot B \\ Z & \, = \, 0 {,} 0193339 \ times R \, + \, 0 {,} 1191920 \ times G \, + \, 0 {,} 9503041 \ times B \ end {aligned}}}

The Lab values are calculated from these XYZ values.

Color examples

This table shows the extremely possible sRGB and CMYK colors for 36 Hue values in steps of 10 (Hue = 10… 360, see color wheel ). The hex RRGGBB color code used is displayed when the mouse pointer is moved over the "Color sample" field.

Extreme RGB and CMYK colors
H	L.	C.	L *	a *	b *	R.	G	B.	H	L.	C.	L *	a *	b *	C.	M.	Y	K
10	55	80	55	78.8	13.9	248	29	112	10	50	75	50	73.9	13.0	2	96	31	1
20th	55	85	55	79.9	29.1	252	51	88	20th	50	75	50	70.5	25.7	3	94	53	1
30th	55	90	55	77.9	45.0	252	30th	60	30th	50	80	50	69.3	40.0	3	94	73	1
40	55	105	55	80.4	67.5	255	16	13	40	50	80	50	61.3	51.4	8th	88	92	1
50	60	95	60	61.1	72.8	250	87	0	50	60	75	60	48.2	57.5	3	69	88	0
60	65	85	65	42.5	73.6	243	123	0	60	60	75	60	37.5	65.0	10	63	100	2
70	75	85	75	29.1	79.9	255	163	0	70	70	75	70	25.7	70.5	6th	46	94	1
80	80	80	80	13.9	78.8	249	187	21st	80	75	80	75	13.9	78.8	9	33	99	1
90	90	85	90	0.0	85.0	255	224	32	90	85	90	85	0.0	90.0	7th	13	99	0
100	95	90	95	−15.6	88.6	245	247	24	100	80	80	80	−13.9	78.8	28	7th	98	0
110	95	95	95	−32.5	89.3	215	255	13	110	75	70	75	−23.9	65.8	43	3	95	0
120	90	95	90	−47.5	82.3	166	249	29	120	70	65	70	−32.5	56.3	55	2	92	0
130	90	105	90	−67.5	80.4	106	255	34	130	60	65	60	−41.8	49.8	72	9	100	1
140	85	95	85	−72.8	61.1	25th	245	83	140	60	65	60	−49.8	41.8	77	2	96	0
150	85	80	85	−69.3	40.0	0	244	131	150	55	65	55	−56.3	32.5	87	6th	94	1
160	85	70	85	−65.8	23.9	0	243	163	160	50	70	50	−65.8	23.9	99	7th	92	1
170	90	60	90	−59.1	10.4	48	255	205	170	50	65	50	−64.0	11.3	99	8th	76	1
180	90	55	90	−55.0	0.0	46	255	224	180	50	60	50	−60.0	0.0	99	9	64	1
190	90	50	90	−49.2	−8.7	64	253	242	190	50	60	50	−59.1	−10.4	100	9	54	1
200	90	50	90	−47.0	−17.1	47	252	255	200	50	60	50	−56.4	−20.5	100	9	42	2
210	85	45	85	−39.0	−22.5	67	234	253	210	55	55	55	−47.6	−27.5	96	6th	31	1
220	80	45	80	−34.5	−28.9	53	217	251	220	55	60	55	−46.0	−38.6	100	5	17th	0
230	75	45	75	−28.9	−34.5	44	201	246	230	60	60	60	−38.6	−46.0	93	1	4th	0
240	70	50	70	−25.0	−43.3	0	187	249	240	55	60	55	−30.0	−52.0	95	16	0	0
250	70	50	70	−17.1	−47.0	52	183	255	250	45	55	45	−18.8	−51.7	99	39	0	0
260	65	55	65	−9.6	−54.2	44	166	255	260	45	50	45	−8.7	−49.2	90	47	0	0
270	55	65	55	0.0	-65.0	0	136	245	270	40	50	40	0.0	−50.0	91	59	0	0
280	50	75	50	13.0	−73.9	14th	117	248	280	35	50	35	8.7	−49.2	92	71	0	0
290	40	95	40	32.5	−89.3	0	81	245	290	30th	50	30th	17.1	−47.0	92	81	2	0
300	30th	125	30th	62.5	−108.3	0	21st	250	300	30th	50	30th	25.0	−43.3	84	86	3	1
310	45	115	45	73.9	−88.1	155	33	255	310	30th	55	30th	35.4	−42.1	78	92	0	1
320	50	110	50	84.3	−70.7	203	0	244	320	35	55	35	42.1	−35.4	63	91	0	0
330	60	105	60	90.9	−52.5	255	18th	239	330	40	55	40	47.6	−27.5	49	89	1	0
340	60	90	60	84.6	−30.8	255	42	202	340	40	60	40	56.4	−20.5	91	94	4th	1
350	55	85	55	83.7	−14.8	247	0	161	350	45	70	45	68.9	−12.2	21st	97	2	0
360	55	80	55	80.0	0.0	246	27	136	360	50	75	50	75.0	0.0	3	96	0	0

Notes on the table "Outermost RGB and CMYK colors"

The L / C accuracy is 5.
In accordance with the consideration that blue is darker than yellow, for example, the “outermost” colors have different brightnesses.
Especially in the yellow / orange and blue / green areas, the available color areas ( gamuts ) differ greatly from one another.

The CMYK preview shows an expected print result

Color conversions were made with Adobe Photoshop, RGB ICC profile: sRGB IEC61966-2.1, CMYK ICC profile: FOGRA39 (ISO 12647-2: 2004)

literature

Manfred Richter: Introduction to colorimetry. 1984 ISBN 3-11-008209-8 .

Web links

Commons : Lab color space - collection of images

Main page of Division 1 of the CIE
Bruce Lindbloom under the navigation point "Math" you can find the usual conversion formulas including matrices
Table of contents of DIN EN ISO 11664-4: 2011-07 at Beuth-Verlag
Gernot Hoffmann, CIELAB derivation with numerous graphics and color overviews programmed in Postscript (PDF)
Conversion routines, color database, CIELAB color fan
L * a * b * color space at Konica Minolta

Individual evidence

^ Richard Sewall Hunter: Photoelectric Color-Difference Meter . In: JOSA . 38, No. 7, July 1948, p. 661. (Proceedings of the Winter Meeting of the Optical Society of America)
^ Richard Sewall Hunter: Accuracy, Precision, and Stability of New Photo-electric Color-Difference Meter . In: JOSA . 38, No. 12, December 1948, p. 1094. (Proceedings of the Thirty-Third Annual Meeting of the Optical Society of America)
↑ ^a ^b ^c The spectral background is only symbolic and decorative and does not directly coincide with the spectral colors of the associated wavelength.
↑ EasyRGB , accessed June 16, 2019

[Hunter1948a-1] Richard Sewall Hunter: Photoelectric Color-Difference Meter . In: JOSA . 38, No. 7, July 1948, p. 661. (Proceedings of the Winter Meeting of the Optical Society of America)

[Hunter1948b-2] Richard Sewall Hunter: Accuracy, Precision, and Stability of New Photo-electric Color-Difference Meter . In: JOSA . 38, No. 12, December 1948, p. 1094. (Proceedings of the Thirty-Third Annual Meeting of the Optical Society of America)

[anm1-3] The spectral background is only symbolic and decorative and does not directly coincide with the spectral colors of the associated wavelength.

[4] EasyRGB , accessed June 16, 2019