Newton's rings

Newton's rings between a slightly curved lens (radius of curvature approx. 13 m) and a flat plate, illuminated by the monochrome light of a sodium vapor lamp .

Sketch of the lens and the flat support. The curvature of the lens is shown greatly exaggerated.

Newton's rings between two almost flat surfaces of lenses lying on top of one another.

Newton's rings (also Newton rings , by Isaac Newton named) are light-dark-zones, or interference colors caused by interference arising at the air gap between two reflecting, substantially parallel surfaces.

Formation of rings

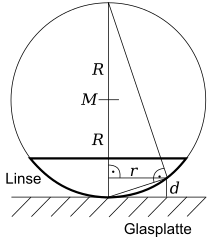
Concentric rings are created in the arrangement described below. A lens with a large radius of curvature R lies with the curved surface on a flat glass plate , between the two boundary surfaces there is an air gap of variable thickness d. If the arrangement is illuminated vertically from above with monochromatic light , concentric light and dark rings appear around the point of contact between the lens and the glass plate , both in reflection and in transparency. With white light, colored rings are created, the intensity of which decreases with the radius.

The colored patterns on soap bubbles and thin layers of oil on water have a similar cause as Newton's rings. In contrast to the Newton rings, the interference does not arise from a thin air gap, but from a thin layer of transparent material.

Explanation

The rings are created by interference at the upper and lower interfaces of the air wedge. Soap bubbles or layers of oil on water in daylight (even better in sunlight ) produce colored rings. The color arises because radiation with a wavelength close to the layer thickness is "interfering" intensified or even extinguished. The layer thickness must be greater than half a wavelength of the light (380 nm to 780 nm). The shorter the wavelength of the light source, the more rings can be seen.

If monochromatic light is shone onto the test arrangement from above, light and dark concentric circles appear alternately due to constructive and destructive interference , the centers of which lie at the point of contact between the lens and the glass plate . The dark rings are created by destructive interference and the light rings by constructive interference. The light waves that are reflected at the interface when passing from the lens into the air interfere with those that are reflected at the interface when passing from the air into the glass plate. If their phase position to each other is 180 °, they cancel each other out, creating dark circles. With mutual reinforcement (phase position 0 °), however, bright rings arise. With increasing distance from the point of support (the distance between the lens surface and the glass plate increases) this condition is repeated several times. This creates several rings that are closer together as the radius increases , as the gradient of the change in distance increases due to the spherical shape of the lens.

Enlargement of the Newton's rings between two planoconvex lenses

If white light is shone in, colored rings are created. The reason for the colors is that the condition for interference is met for different wavelengths with different gap thicknesses. In the image of the glass lenses lying on top of one another, the reflection on the surfaces approaching each other is shown. If the condition for destructive interference is met, the light of the respective color is not reflected. The rest of the spectrum remains and creates the complementary color . The distance between the rings for a certain color is greater, the greater the wavelength of the color. This means that the sequence of colors gradually shifts outwards. In addition, the rings of different colors overlap and colors are created through additive color mixing . In the enlarged section you can see clearly separated red and green stripes on the inner, wide rings. To the left, the two colors overlap to form a yellow. On the very outside they appear again separately, but in the reverse order.

Deriving the equation

Construction aid to explain the interference

The path s that all rays of light travel through the air is

${\displaystyle s=2d}$.

If one takes into account the phase shift of 180 ° in the reflection on the optically denser medium, the following applies:

${\displaystyle s=2d+{\frac {\lambda }{2}}}$.

The prerequisite for extinction is that the path is an odd multiple of half the wavelength. This means:

${\displaystyle s={\frac {2k+1}{2}}\lambda }$

If one sets both formulas the same, the result is:

${\displaystyle 2d+{\frac {\lambda }{2}}={\frac {2k+1}{2}}\lambda }$

Simplified:

${\displaystyle 2d=k\lambda }$

According to the height theorem :

${\displaystyle r^{2}=d(2R-d)}$

Since d is much smaller than R, we get:

${\displaystyle r^{2}=2dR}$

So:

${\displaystyle d={\frac {r^{2}}{2R}}}$

Inserted into the simplified equation:

${\displaystyle 2{\frac {r^{2}}{2R}}=k\lambda }$

Abbreviated:

${\displaystyle {\frac {r^{2}}{R}}=k\lambda }$

The following results for the radius of the k-th ring:

${\displaystyle r={\sqrt {k\lambda R}}}$

k is the number of the (dark) circle counted from the center

λ is the wavelength of the light that creates the ring

R is the radius of curvature of the lens

Occur

Mica disc ( muscovite ) with Newtonian rings.

• Optical surfaces that touch or face each other, such as with non-cemented lenses. This can be avoided by cracking open or cementing it.
• Lenses, mirror blanks and plane-parallel plates that are placed in test glass molds (quality control)
• Color fringes occur on slides framed in glass. The Newtonian rings are created by the air layer of different thicknesses between the glass and the slide film. The effect can be avoided by rough surfaces of so-called anti-Newton glass .
• One can see Newton's rings in the air layer between mica surfaces in minerals like muscovite .

Benefits and uses

The effect is used to judge the quality of the shape of lenses. The number and symmetry of the rings to be observed when the lens is placed in a reference mold sometimes serves as a measure of the quality. Using the rings or “contour lines”, fluctuations in the thickness of thin layers can also be estimated. The effect is also used for non-contact quality testing of high and top quality mirrors, especially for mirror telescopes .

An early form of the reflex sight was also based on this effect.

Web links

Commons : Newton's Rings  - collection of images, videos and audio files

• Newton's Rings ( Newton-gyűrűk , Hungarian) Video of two simple experiments