Periodic orbit

The movement of a harmonic oscillator results in a periodic orbit in phase space .

The orbit of a planet is not exactly periodic because of the rotation of the apse , the animation exaggerates this effect very much.

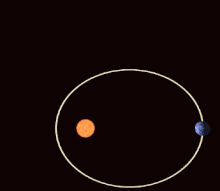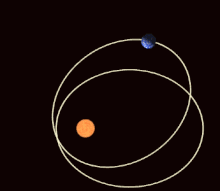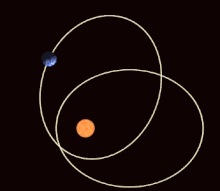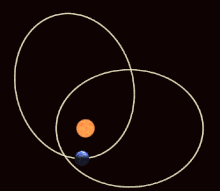
In the mathematical theory of dynamic systems , a periodic orbit or a periodic orbit (also: closed orbit ) is a trajectory that always returns to its starting point after a certain period of time (the "period"), which is therefore closed in itself and thus one corresponds to repetitive, periodic movement. Points on periodic orbits are called periodic points .

Examples of periodic orbits are the movement of a harmonic oscillator or the planetary orbits (which, however, are no longer exactly periodic if one takes into account the rotation of the apses ).

definition

In a time-continuous dynamic system, i. H. with : ${\displaystyle t\in \mathbb {R} }$

${\displaystyle \varphi \colon X\times \mathbb {R} \to X}$

a flow on a state space . The orbit ${\displaystyle X}$

${\displaystyle {\mathcal {O}}(x,\varphi ):=\left\{\varphi (x,t)|t\in \mathbb {R} \right\}}$

of a point is called a periodic orbit if there is one such that ${\displaystyle x\in X}$ ${\displaystyle T>0}$

${\displaystyle \varphi (x,t+T)=\varphi (x,t)}$

applies to all . The smallest possible such positive number is called the period of the orbit. ${\displaystyle t\in \mathbb {R} }$ ${\displaystyle T}$

The same definition is used for discrete dynamic systems, here then and are whole numbers . ${\displaystyle t}$ ${\displaystyle T>0}$

Periodic orbits of temporally continuous systems have the topology of a circle, while in discrete systems (iterated mapping) they consist of a number of points corresponding to the period, which are mapped onto one another cyclically.

Seifert conjecture

The question of whether the flows of all continuous vector fields on the 3-dimensional sphere have a periodic orbit became known as the Seifert conjecture . There are counterexamples to this assumption even with arbitrarily strong conditions on the differentiability of the vector field.

Reeb orbits

The counterexamples to the Seifert conjecture show that vector fields on the 3-dimensional sphere can have very pathological dynamics. There is a more regular behavior for so-called Reeb vector fields of the standard contact structure on the 3-sphere. For these it can be proven that there are always periodic orbites (so-called Reeb orbites ) and methods (e.g. contact homology ) are available for counting the periodic orbites.

Web links

• Periodic orbit (Scholarpedia)

Individual evidence

1. ↑ Lexicon of Physics. Spectrum Academic Publishing House, Heidelberg 1998.
2. ↑ Article with counterexamples:
   • V. Ginzburg, B. Gürel: A- smooth counterexample to the Hamiltonian Seifert conjecture in ]. ${\displaystyle C^{2}}$ ${\displaystyle R^{4}}$In: Ann. of Math. (2) 158, no. 3, 2003, pp. 953-976.
   • J. Harrison: Counterexamples to the Seifert conjecture. In: Topology. 27, no. 3, 1988, pp. 249-278. ${\displaystyle C^{2}}$
   • G. Kuperberg: A volume-preserving counterexample to the Seifert conjecture. In: Comment. Math. Helv. 71, no. 1, 1996, pp. 70-97.
   • K. Kuperberg: A smooth counterexample to the Seifert conjecture. In: Ann. of Math. (2) 140, no. 3, 1994, pp. 723-732.
   • G. Kuperberg, K. Kuperberg: Generalized counterexamples to the Seifert conjecture . In: Ann. of Math. (2) 143, no. 3, 1996, pp. 547-576.
   • H. Seifert: Closed integral curves in 3-space and isotopic two-dimensional deformations. In: Proc. Amer. Math. Soc. 1, 1950, pp. 287-302.
   • PA Schweitzer: Counterexamples to the Seifert conjecture and opening closed leaves of foliations. In: Ann. of Math. (2) 100, 1974, pp. 386-400.