Pseudopotential

Comparison of a 5s wave function in the Coulomb potential of the nucleus (blue) with one in the pseudopotential (red). The real and the pseudo wave function and the potentials themselves agree above the cutoff radius . ${\displaystyle r_{c}}$

The pseudopotential formalism in quantum mechanics is an approach to approximate the computationally close to the nucleus (non-valence) electrons of an atom or ion as well as the atomic nucleus through an effective potential. This approximation is possible because the electrons close to the nucleus hardly contribute to chemical bonds. However, valence electrons are orthogonal to all electrons close to the nucleus, which leads to a strong oscillation close to the nucleus and therefore to a high computing effort. In addition, electrons close to the nucleus have high energy, which means a short wavelength, which means that a high spatial resolution must be expected. By cleverly choosing an empirical potential, the effort required to solve the Schrödinger equation can be massively reduced. The wave function of the valence electrons is then orthogonal to all nuclear states.

The pseudopotential was first introduced in 1934 by Hans Hellmann . The method found widespread use in band structure calculations in solid state physics , with James C. Phillips being a pioneer in the late 1950s (later with Marvin Cohen , Volker Heine, and others).

Approximations

1. A one-electron picture is used to split electrons into nucleus and valence sets.
2. Frozen-Core Approximation : The one-electron states of the core part are constant.
3. The . Small Core Appr and (small core approximation) assumes that the core and valence states have no significant overlap in order for the exchange-correlation potential (see DFT (QM) ) where: ; This is not always true, and then the non-linear core corrections technique (Louie, Froyen, Cohen, 1982) can be used to improve the results. ${\displaystyle E_{xc}(n_{kern}+n_{valenz})=E_{xc}(n_{kern})+E_{xc}(n_{valenz})}$

species

Two classes of pseudopotentials (PP) are used: Norm-conserving PP and Ultrasoft PP.

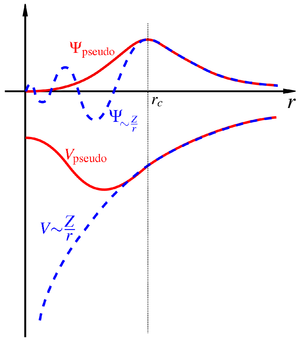
Norm-conserving (norm-maintaining) PP: Outside a certain radius (cutoff radius) the PP wave functions are identical to the real (all-electron) wave functions. They were first proposed in 1979 by DR Hamann, M. Schlueter and C. Chiang. One example is the BHS-PP by Bachelet, Hamann and Schlüter (1982)

Ultrasoft PP was introduced by David Vanderbilt and has the advantage that the wave functions are even “smoother”, that is, require a significantly lower number of plane waves for the description for the same accuracy, and thus the computing time is even less. A disadvantage of these potentials is that the atomic orbitals no longer form an orthonormal system.

Both types of pseudopotentials are “non-local”, which means that the potential depends on the angular momentum quantum number . ${\displaystyle l}$

literature

• Walter A. Harrison (1966): Pseudopotentials in the theory of metals, Frontiers in Physics, University of Virginia
• David Brust, Bernie Alder (Editor) (1968) The Pseudopotential Method and the Single-Particle Electronic Excitation Spectra of Crystals , Methods in Computational Physics 8: 33-61
• Volker Heine (1970), The Pseudopotential Concept , Solid State Physics 24: 1–36,
• Warren E. Pickett (April 1989): Pseudopotential methods in condensed matter applications , Computer Physics reports 9 (3): 115-197

See also

• Density functional theory (quantum physics)

Individual evidence

1. ↑ Hans Hellmann A New Approximation Method in the Problem of Many Electrons , Journal of Chemical Physics ( Karpow ‐Institute for Physical Chemistry, Moscow), Volume 3, 1935, p. 61, Hans Hellmann, W. Kassatotschkin Metallic Binding According to the Combined Approximation Procedure , Journal of Chemical Physics (Karpow Institute for Physical Chemistry, Moscow), Volume 4, 1936, p. 324.
2. ↑ Steven G. Louie, Sverre Froyen, Marvin L. Cohen; Nonlinear ionic pseudopotentials in spin-density-functional calculations, Physical Review B, American Physical Society, Volume 26, 1982, pp. 1738-1742.
3. ^ DR Hamann, M. Schlueter, C. Chiang: Norm-Conserving Pseudopotentials, Physical Review Letters., Volume 43, 1979, pp. 1494-1497.
4. ^ GB Bachelet, DR Hamann, M. Schlueter: Pseudopotentials that work: From H to Pu ", Physical Review B, Volume 26, 1982, pp. 4199-4228.
5. ^ Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B, Vol. 41, 1990, pp. 7892-7895.