QuickHull
QuickHull is an algorithm to compute the convex hull of any finite set of points in two- or three-dimensional space. The convex hull of a set of points is described by a closed polygon , which represents the connection of all extreme points of the set, and thus includes all points of the set. A frequently used intuitive explanation of this cover is a rubber band, which is stretched around the point set. If it rests tightly on all outer points, this forms the convex envelope of the point set.
Naming and origin
The name QuickHull is derived from the similarity to Quicksort , an algorithm for sorting any quantity. It is first mentioned in the book Computational geometry by Franco Preparata and Michael Shamos, in which the two authors present the algorithm described here, which takes up the ideas of other authors.
Basic idea
The algorithmic idea for QuickHull comes from the “ divide and conquer ” principle, which is often used in computer science. It describes how to break down the problem into several small problems and then solve them recursively using the same algorithm . In this context, attempts are often made to choose the division so cleverly that it already eliminates a large number of invalid solution sets. With this type of structure, algorithms that have been designed according to this principle can often be implemented in a simple and easy-to-read manner, since they have an understandable recursive structure.
example
The algorithm operates on any finite set of points. There are no special requirements for the arrangement or number of points. A symmetrical arrangement of the points, however, has a higher probability of leaving the best case (best case) transit time limit of and being significantly slower.
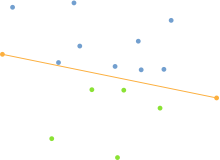
To determine the first division of the set, the two extreme points of the X-axis are searched for. So those points which are furthest left and furthest right. These points can already be added to the polygon of the convex hull, since as extreme points they are guaranteed to be part of the same.
The two points found form a straight line that divides the set of points into two areas. All points to the left of the line represent one set and all points to the right of the line represent the other. In this context, right and left result from the angle between the direction vector of the dividing line and the vector defined by the starting point of the straight line and the point to be checked. If this angle is smaller than 180 °, then the point is considered to be to the right of the straight line, for angles greater than 180 ° it is considered to be to the left of it.
The two sets of points separated by this straight line are now processed recursively with the QuickHull algorithm. In this example only the left part of the point set is considered further. All statements made apply equally to the right part.
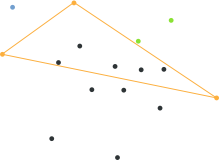
Within the set of points under consideration, that point is determined which has the maximum distance from the straight line. This is obviously also a component of the traverse sought. Together with the start and end point of the straight line, a triangle is created.
The triangle is made up of three points, all of which are part of the convex hull polygon. For this reason, all points inside this triangle cannot be part of this polygon, since they are already inside it. All points within this triangle can therefore be ignored for further recursive calls to the algorithm.
The straight lines resulting from the sides of the triangle are now regarded as new dividing lines for the point set. All points to the left of the triangle represent one set, all points to the right of the triangle represent the other.
This recursive division and determination of further points is repeated until only the start and end point of the dividing line are part of the point set to be considered, because in this case it is clear that this line represents a segment of the desired polygon.
literature
- ^ Franco P. Preparata , Michael Ian Shamos : Computational Geometry . An Introduction. 1st edition. Springer-Verlag , 1985, ISBN 0-387-96131-3 .
- ^ William F. Eddy : A New Convex Hull Algorithm for Planar Sets . In: ACM Transactions on Mathematical Software . 3, 1977, pp. 393-403.
- ↑ Alex Bykat : Convex Hull of a Finite Set of Points in Two Dimensions . In: Information Processing Letters . 7, 1978, pp. 296-298.
- ^ PJ Green , BW Silverman : Constructing the Convex Hull of a Set of Points in the Plane . In: Computer Journal . 22, 1979, pp. 262-266.