Remez algorithm

The Remez algorithm in approximation theory is a minimax approximation algorithm. As such, it minimizes the maximum absolute difference between the polynomial sought (given maximum degree ) and the given (in an interval) continuous function . It is named after the Soviet mathematician Yevgeny Jakowlewitsch Remes , who introduced it in 1934. ${\displaystyle p}$ ${\displaystyle n}$ ${\displaystyle f}$

The algorithm relies on the alternant theorem by Pafnuti Lwowitsch Tschebyschow , by iteratively evaluating the mentioned difference at support points in the interval and calculating new support points from this . ${\displaystyle n+2}$ ${\displaystyle n+2}$

algorithm

Given:	An interval and a continuous function ; ${\displaystyle [a,b]\subset \mathbb {R} }$ ${\displaystyle f\colon [a,b]\to \mathbb {R} }$
	also a maximum polynomial degree . ${\displaystyle n}$
Searched:	A polynomial of degree at most which ${\displaystyle p(x)\in \mathbb {R} [x]}$ ${\displaystyle n}$
	${\displaystyle \max _{a\leq x\leq b}|f(x)-p(x)|}$
	minimized.

From the alternant theorem it follows that the polynomial in the Limes is uniquely determined and that there are points for which applies ${\displaystyle n+2}$ ${\displaystyle (a\leq )\;x_{0}<x_{1}<\ldots <x_{n+1}\;(\leq b)}$

${\displaystyle f(x_{i})-p(x_{i})=\pm (-1)^{i}\cdot E}$

with the deviation ( supremum norm ). ${\displaystyle E:=\max _{a\leq x\leq b}|f(x)-p(x)|=\|f-p\|_{\infty }}$

The polynomial we are looking for is with

${\displaystyle p(x)=:c_{0}+c_{1}\cdot x+\,...\,+c_{n}\cdot x^{n}}$

designated. So it applies to the unknown ${\displaystyle n+1}$

${\displaystyle c_{0},c_{1},\ldots ,c_{n}}$

to determine.

preparation

One begins with the extreme places of the Chebyshev polynomial of the first kind of degree ${\displaystyle n+1}$

${\displaystyle x_{i}={\frac {a+b}{2}}-{\frac {b-a}{2}}\cdot \cos \left({\frac {i\pi }{n+1}}\right)}$   with   . ${\displaystyle i=0,\ldots ,n+1}$

Such a set of points is called a "reference". It is

${\displaystyle a=x_{0}<x_{1}<\,...\,<x_{n+1}=b}$.

iteration

Compute an approximation on the reference

We are looking for the polynomial of the degree whose error function alternates on the reference obtained in the previous step . I.e. are sought ${\displaystyle p(x)}$ ${\displaystyle \leq n}$ ${\displaystyle f(x)-p(x)}$ ${\displaystyle x_{0}<x_{1}<\dots <x_{n+1}}$

${\displaystyle c_{0},c_{1},\ldots ,c_{n}}$   and   . ${\displaystyle E}$

With

${\displaystyle p(x_{i})+(-1)^{i}\cdot E=f(x_{i})}$   for   . ${\displaystyle i=0,\ldots ,n+1}$

This task has only the reference as input and only the values of the function . It can also be formulated as an optimization task, namely as the best approximation on the reference, and can be clearly solved. ${\displaystyle f}$ ${\displaystyle n+2}$ ${\displaystyle f(x_{i})}$

The system of equations to be solved in matrix representation :

${\displaystyle \left({\begin{matrix}1&x_{0}&\cdots &x_{0}^{n}&1\\1&x_{1}&\cdots &x_{1}^{n}&-1\\\vdots &\vdots &\vdots &\vdots &\vdots \\1&x_{n}&\cdots &x_{n}^{n}&(-1)^{n}\\1&x_{n+1}&\cdots &x_{n+1}^{n}&(-1)^{n+1}\\\end{matrix}}\right){\begin{pmatrix}c_{0}\\c_{1}\\\vdots \\c_{n}\\E\end{pmatrix}}={\begin{pmatrix}f(x_{0})\\f(x_{1})\\\vdots \\f(x_{n})\\f(x_{n+1})\\\end{pmatrix}}}$

This gives you new coefficients ${\displaystyle n+1}$

${\displaystyle c_{0},c_{1},\ldots ,c_{n}}$

for the polynomial and a new "reference deviation"  . ${\displaystyle p(x)}$ ${\displaystyle E}$

Find local extreme points of the error function with as a polynomial of degree 2. ${\displaystyle {\tilde {x}}_{1},{\tilde {x}}_{2}}$ ${\displaystyle 1/(37/12-x)-p(x)}$ ${\displaystyle {\color {Blue}p}}$

Replace the reference with extreme places

Starting from the polynomial , extreme points of the error function apply ${\displaystyle p(x)}$ ${\displaystyle n+2}$ ${\displaystyle {\tilde {x}}_{0},{\tilde {x}}_{1},\ldots ,{\tilde {x}}_{n+1}}$

${\displaystyle f(x)-p(x)}$

to find. If it is differentiable , extreme points can often be obtained by setting the derivative function to zero. ${\displaystyle f}$ ${\displaystyle f'-p'}$

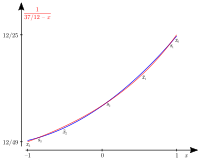
In any case, the interval can be divided into the sub-intervals that can be specified by the current error function as follows. Since with is also continuous, there are, according to the intermediate value theorem, for all zeros of the error function (in the figure, interfaces of the red function with the blue polynomial ) in the interval , since the sign of the error function alternates at the places ( ). Comes in two adjacent intervals and only one zero respectively , then the error function in the interval is only non-negative, or only non-positive. (But even if there are several zeros, the other applies - the extremes may just not be so pronounced.) Because of the continuity of the error function, according to the principle of minimum and maximum, there are (local) extreme points in each sub-interval . The result is the first extremum, the following extremes alternate between maximum and minimum up to the last extremum . ${\displaystyle [a,b]}$ ${\displaystyle [s_{i},s_{i+1}]}$ ${\displaystyle f}$ ${\displaystyle f-p}$ ${\displaystyle i=1,\ldots ,n+1}$ ${\displaystyle s_{i}}$ ${\displaystyle f}$ ${\displaystyle p}$ ${\displaystyle [x_{i-1},x_{i}]}$ ${\displaystyle x_{i}}$ ${\displaystyle \operatorname {sgn}(f-p)(x_{i-1})=-\operatorname {sgn}(f-p)(x_{i})}$ ${\displaystyle [x_{i-1},x_{i}]}$ ${\displaystyle [x_{i},x_{i+1}]}$ ${\displaystyle s_{i}\in [x_{i-1},x_{i}]}$ ${\displaystyle s_{i+1}\in [x_{i},x_{i+1}]}$ ${\displaystyle [s_{i},s_{i+1}]}$ ${\displaystyle [s_{i},s_{i+1}]}$ ${\displaystyle {\tilde {x}}_{i}}$ ${\displaystyle {\tilde {x}}_{0}:=a}$ ${\displaystyle {\tilde {x}}_{n+1}:=b}$

In addition, the (absolute) quality of the approximation occurs in the form of . If it is unsatisfactory, you can iterate with the newly acquired reference . It can also be interesting to increase the degree of approximation by inserting intermediate points in the reference. The Example 2 in the article alternant theorem shows how the quality of the local best approximation depends on the degree of the polynomial. ${\displaystyle \max _{i}|f({\tilde {x}}_{i})-p({\tilde {x}}_{i})|}$ ${\displaystyle {\tilde {x}}_{0},{\tilde {x}}_{1},\ldots ,{\tilde {x}}_{n+1}}$ ${\displaystyle n}$

Convergence speed

Under suitable conditions regarding the function , the method converges locally quadratically. ${\displaystyle f}$

literature

• Leçons sur l'approximation des fonctions d'une variable réellehttp: //vorlage_digitalisat.test/1%3D~GB%3D~IA%3Dleonssurlappro00lavauoft~MDZ%3D%0A~SZ%3D~doppelseiten%3D~LT%3D%27%27Le%C3%A7ons%20sur%20l% 27approximation% 20des% 20fonctions% 20d% 27une% 20variable% 20r% C3% A9elle% 27% 27 ~ PUR% 3D Paris, Gauthier-Villars, 1919, 1952

• C. de Boor, A. Pinkus: Proof of the conjectures of Bernstein and Erdös concerning the optimal nodes for polynomial interpolation . In: Journal of Approximation Theory . 24, 1978, pp. 289-303. doi : 10.1016 / 0021-9045 (78) 90014-X .

References and comments

1. ↑ E. Ya. Remez, "Sur la détermination des polynômes d'approximation de degré donnée", Comm. Soc. Math. Kharkov 10 , 41 (1934);
   "Sur un procédé convergent d'approximations successives pour déterminer les polynômes d'approximation", Compt. Rend. Acad. Sc. 198: 2063 (1934);
   "Sur le calcul effectiv des polynômes d'approximation de Chebyshev", Compt. Rend. Acad. Sc. 199: 337-340 (1934).
2. ↑ René Grothmann Lecture Notes Approximation Theory 1.69. definition
3. ↑ The given matrix has Vandermonde matrices as sub-matrices.
   The solution of the equation system costs many standard packages , but it can also be done in (see polynomial interpolation # Newton's algorithm ). ${\displaystyle {\mathcal {O}}(n^{3})}$ ${\displaystyle {\mathcal {O}}(n^{2})}$
4. ↑ René Grothmann Lecture Notes Approximation Theory 1.71. comment