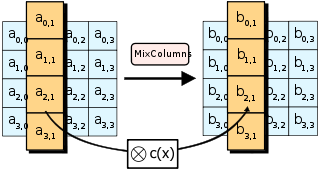
Rijndael MixColumns

The MixColumns step is a step in the Rijndael algorithm (AES).

In MixColumnsstep, each column of the state is linked with c (x) .

The matrix multiplication

In this step a matrix multiplication of a column vector of the state takes place with an MDS matrix so that all 4 input bytes influence each output byte.

${\displaystyle {\begin{pmatrix}2&3&1&1\\1&2&3&1\\1&1&2&3\\3&1&1&2\end{pmatrix}}{\begin{pmatrix}a_{0,i}\\a_{1,i}\\a_{2,i}\\a_{3,i}\end{pmatrix}}={\begin{pmatrix}b_{0,i}\\b_{1,i}\\b_{2,i}\\b_{3,i}\end{pmatrix}}}$

The arithmetic does not take place on the natural numbers , but on the Galois field of Rijndael.

The Galois body of the Rijndael

The Galois body of the Rijndael is the Galois body . ${\displaystyle GF(2^{8})}$

${\displaystyle GF(2^{8})}$is the set of all polynomials of a maximum of 7th degree with coefficients from the remainder class field . ${\displaystyle \mathbb {F} _{2}=\mathbb {Z} /2\mathbb {Z} }$

A general polynomial from has the form As is easy to see, each of these polynomials can be represented by a byte , with the th bit representing the coefficient . ${\displaystyle GF(2^{8})}$ ${\displaystyle a_{7}x^{7}+a_{6}x^{6}+a_{5}x^{5}+a_{4}x^{4}+a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0}\ \ (a_{i}\in \mathbb {F} _{2}).}$ ${\displaystyle i}$ ${\displaystyle a_{i}}$

The addition to is defined as an XOR operation analogous to the body , it takes place coefficient-wise or bit-wise. The subtraction is the same as the addition because the XOR operation is its own inverse function. Example: ${\displaystyle \oplus }$ ${\displaystyle GF(2^{8})}$ ${\displaystyle \mathbb {F} _{2}}$

${\displaystyle (x^{5}+x^{4}+x^{3})-(x^{7}+x^{5}+x^{3}+x+1)=(x^{5}+x^{4}+x^{3})+(x^{7}+x^{5}+x^{3}+x+1)=x^{7}+x^{4}+x+1}$

The multiplication ( ) takes place modulo the irreducible polynomial . To do this, multiply the two polynomials and then calculate the remainder by means of a polynomial division. ${\displaystyle \cdot }$ ${\displaystyle x^{8}+x^{4}+x^{3}+x+1}$

example

The calculation of with is now carried out as an example . Unless otherwise stated, numbers are in hexadecimal . ${\displaystyle b_{0,1}}$ ${\displaystyle {\begin{pmatrix}a_{0,i}\\a_{1,i}\\a_{2,i}\\a_{3,i}\end{pmatrix}}={\begin{pmatrix}{\rm {d4}}\\32\\{\rm {f4}}\\{\rm {ae}}\end{pmatrix}}}$

${\displaystyle {\begin{pmatrix}2&3&1&1\\1&2&3&1\\1&1&2&3\\3&1&1&2\end{pmatrix}}{\begin{pmatrix}{\rm {d4}}\\32\\{\rm {f4}}\\{\rm {ae}}\end{pmatrix}}={\begin{pmatrix}b_{0,i}\\b_{1,i}\\b_{2,i}\\b_{3,i}\end{pmatrix}}}$

It follows ${\displaystyle b_{0,1}=(2\cdot {\rm {{d4})+(3\cdot 32)+(1\cdot {\rm {{f4})+(1\cdot {\rm {{ae})}}}}}}}$

The terms and are trivial. ${\displaystyle 1\cdot {\rm {{f4}={\rm {f4}}}}}$ ${\displaystyle 1\cdot {\rm {{ae}={\rm {ae}}}}}$

${\displaystyle {\begin{aligned}2\cdot {\rm {d4}}&=00000010_{2}\cdot 11010100_{2}\\&=x\cdot (x^{7}+x^{6}+x^{4}+x^{2})\\&=(x^{8}+x^{7}+x^{5}+x^{3})\ {\bmod {\ }}(x^{8}+x^{4}+x^{3}+x+1)\\&=110101000_{2}\ {\bmod {\ }}100011011_{2}\\&=110101000_{2}\ [phone]_{2}\\&=010110011_{2}=b3\end{aligned}}}$

${\textstyle {\begin{aligned}3\cdot 32&=00000011_{2}\cdot 00110010_{2}\\&=(x+1)\cdot (x^{5}+x^{4}+x)\\&=(x^{6}+x^{5}+x^{2}+x^{5}+x^{4}+x)\ {\bmod {\ }}(x^{8}+x^{4}+x^{3}+x+1)\\&=(x^{6}+x^{4}+x^{2}+x)\ {\bmod {\ }}(x^{8}+x^{4}+x^{3}+x+1)\\&=01010110_{2}\ {\bmod {\ }}100011011_{2}\\&=01010110_{2}=56\end{aligned}}}$

This results with XOR : ${\displaystyle b_{0,1}=b3+56+{\rm {{f4}+{\rm {{ae}={\rm {bf}}}}}}}$

The reverse of the MixColumns step

Decryption can be done in the same way as encryption in this step. However, you have to multiply with the inverse matrix. It reads (numbers in hexadecimal ):

${\displaystyle {\begin{pmatrix}E&B&D&9\\9&E&B&D\\D&9&E&B\\B&D&9&E\end{pmatrix}}}$

there

${\displaystyle {\begin{pmatrix}2&3&1&1\\1&2&3&1\\1&1&2&3\\3&1&1&2\end{pmatrix}}{\begin{pmatrix}E&B&D&9\\9&E&B&D\\D&9&E&B\\B&D&9&E\end{pmatrix}}={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}}$

Implementation options

The fact that in the Rijndael only multiplications with , or take place during encryption means that the algorithm can be implemented very efficiently and easily on the computer. ${\displaystyle 1}$ ${\displaystyle x}$ ${\displaystyle (x+1)}$

Multiplication by is trivial. The multiplication with means a shift by 1 bit to the left in the binary representation (the modulo calculation must be considered separately), and the multiplication with can be split into a multiplication with and subsequent addition with itself. If an overflow occurs, you still have to XOR the intermediate result in order to get the correct result. ${\displaystyle 1}$ ${\displaystyle x}$ ${\displaystyle (x+1)}$ ${\displaystyle x}$ ${\displaystyle 1b}$

The following C code only serves as an example for a possible simple implementation and does not represent a safe reference implementation.

unsigned char mul123(unsigned char a, unsigned char b){
  if(b==1){
    return a;
  }
  else if(b==2){
    unsigned char c = a << 1;
    if(a & 0x80)
      c ^= 0x1b;
    return c;
  }
  else if(b==3){
    return mul123(a, 2) ^ a;
  }
  else exit{EXIT_FAILURE};
}

When decoding, however, multiplication with other numbers is also required, where the above approach becomes useless.

The following applies to suitable is bijective. The inverse function is called . Such a suitable one is called a generator, examples for this would be the 3 or the 5, but there are a few more. ${\displaystyle e\in GF(2^{8})}$ ${\displaystyle exp:GF(2^{8})\backslash \{0\}\to GF(2^{8})\backslash \{0\},x\mapsto e^{x}}$ ${\displaystyle ln}$ ${\displaystyle x}$

Proof: At last, this can be checked by recalculating. ${\displaystyle GF(2^{8})}$

Since is bijective, applies to : ${\displaystyle exp}$ ${\displaystyle a,b\in GF(2^{8})\backslash \{0\}}$

${\displaystyle a\cdot b=e^{ln(a\cdot b)}=e^{ln(a)+ln(b)}}$

for true ${\displaystyle a=0\vee b=0}$ ${\displaystyle a\cdot b=0}$

If we now create an exponential and logarithmic table for a generator for the multiplication, we can use this to effectively implement the general multiplication . The table can either be calculated at runtime - generator 3 is available with the above function - or it can be in the source code. ${\displaystyle GF(2^{8})}$

unsigned char RijndaelGaloisMul(unsigned char a, unsigned char b){
  if(a && b) //falls a != 0 und b != 0
    return exp_table[(ln_table[a] + ln_table[b]) % 0xff];
  else
    return 0;
}

Below is the exponential and logarithmic table for generator 3:

 Potenzen:
   | *0  *1  *2  *3  *4  *5  *6  *7  *8  *9  *a  *b  *c  *d  *e  *f |
 ----------------------------------------------------------------------
 0*| 01  03  05  0f  11  33  55  ff  1a  2e  72  96  a1  f8  13  35 |0*
 1*| 5f  e1  38  48  d8  73  95  a4  f7  02  06  0a  1e  22  66  aa |1*
 2*| e5  34  5c  e4  37  59  eb  26  6a  be  d9  70  90  ab  e6  31 |2*
 3*| 53  f5  04  0c  14  3c  44  cc  4f  d1  68  b8  d3  6e  b2  cd |3*
 4*| 4c  d4  67  a9  e0  3b  4d  d7  62  a6  f1  08  18  28  78  88 |4*
 5*| 83  9e  b9  d0  6b  bd  dc  7f  81  98  b3  ce  49  db  76  9a |5*
 6*| b5  c4  57  f9  10  30  50  f0  0b  1d  27  69  bb  d6  61  a3 |6*
 7*| fe  19  2b  7d  87  92  ad  ec  2f  71  93  ae  e9  20  60  a0 |7*
 8*| fb  16  3a  4e  d2  6d  b7  c2  5d  e7  32  56  fa  15  3f  41 |8*
 9*| c3  5e  e2  3d  47  c9  40  c0  5b  ed  2c  74  9c  bf  da  75 |9*
 a*| 9f  ba  d5  64  ac  ef  2a  7e  82  9d  bc  df  7a  8e  89  80 |a*
 b*| 9b  b6  c1  58  e8  23  65  af  ea  25  6f  b1  c8  43  c5  54 |b*
 c*| fc  1f  21  63  a5  f4  07  09  1b  2d  77  99  b0  cb  46  ca |c*
 d*| 45  cf  4a  de  79  8b  86  91  a8  e3  3e  42  c6  51  f3  0e |d*
 e*| 12  36  5a  ee  29  7b  8d  8c  8f  8a  85  94  a7  f2  0d  17 |e*
 f*| 39  4b  dd  7c  84  97  a2  fd  1c  24  6c  b4  c7  52  f6  01 |f*

 Logarithmen:
   | *0  *1  *2  *3  *4  *5  *6  *7  *8  *9  *a  *b  *c  *d  *e  *f |
 ----------------------------------------------------------------------
 0*| --  00  19  01  32  02  1a  c6  4b  c7  1b  68  33  ee  df  03 |0*
 1*| 64  04  e0  0e  34  8d  81  ef  4c  71  08  c8  f8  69  1c  c1 |1*
 2*| 7d  c2  1d  b5  f9  b9  27  6a  4d  e4  a6  72  9a  c9  09  78 |2*
 3*| 65  2f  8a  05  21  0f  e1  24  12  f0  82  45  35  93  da  8e |3*
 4*| 96  8f  db  bd  36  d0  ce  94  13  5c  d2  f1  40  46  83  38 |4*
 5*| 66  dd  fd  30  bf  06  8b  62  b3  25  e2  98  22  88  91  10 |5*
 6*| 7e  6e  48  c3  a3  b6  1e  42  3a  6b  28  54  fa  85  3d  ba |6*
 7*| 2b  79  0a  15  9b  9f  5e  ca  4e  d4  ac  e5  f3  73  a7  57 |7*
 8*| af  58  a8  50  f4  ea  d6  74  4f  ae  e9  d5  e7  e6  ad  e8 |8*
 9*| 2c  d7  75  7a  eb  16  0b  f5  59  cb  5f  b0  9c  a9  51  a0 |9*
 a*| 7f  0c  f6  6f  17  c4  49  ec  d8  43  1f  2d  a4  76  7b  b7 |a*
 b*| cc  bb  3e  5a  fb  60  b1  86  3b  52  a1  6c  aa  55  29  9d |b*
 c*| 97  b2  87  90  61  be  dc  fc  bc  95  cf  cd  37  3f  5b  d1 |c*
 d*| 53  39  84  3c  41  a2  6d  47  14  2a  9e  5d  56  f2  d3  ab |d*
 e*| 44  11  92  d9  23  20  2e  89  b4  7c  b8  26  77  99  e3  a5 |e*
 f*| 67  4a  ed  de  c5  31  fe  18  0d  63  8c  80  c0  f7  70  07 |f*

Web links

• AES encryption tutorial
• FIPS PUB 197: the official AES standard ( PDF file; 273 kB)