Baer-Epstein's theorem

In mathematics , Baer-Epstein's theorem is a fundamental theorem in the topology of surfaces . It says that homotopic curves on surfaces are even isotopic, and that homotopic homeomorphisms of surfaces are always isotopic. It is named after Reinhold Baer and David Epstein .

Curves on surfaces

Two simple closed curves on the torus.

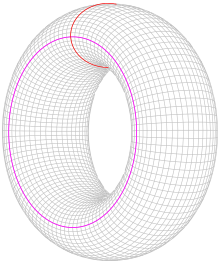
A simple closed curve on a surface is an embedding . Two curves ${\displaystyle F}$ ${\displaystyle i\colon S^{1}\to F}$

${\displaystyle i_{0},i_{1}\colon S^{1}\to F}$

are called homotop if there is a continuous figure

${\displaystyle H\colon S^{1}\times \left[0,1\right]\to F}$

with there. Two simple closed curves are called isotopes if there is a homotopy in which the curve is common to all ${\displaystyle H(x,0)=i_{0}(x),H(x,1)=i_{1}(x)\ \forall \ x\in S^{1}}$ ${\displaystyle i_{0},i_{1}}$ ${\displaystyle t\in \left[0,1\right]}$

${\displaystyle i_{t}(.)=H(.,t)\colon S^{1}\to F}$

is a simple closed curve (i.e. an embedding).

Baer proved in 1928 that two homotopic, simple closed curves must also be isotopic on a closed , orientable surface. This theorem was generalized by Epstein in 1966 to non-compact surfaces with non-empty margins; the most general possible formulation is the following.

Proposition : Let be any surface, let ${\displaystyle F}$

${\displaystyle i_{0},i_{1}\colon S^{1}\to F}$

two base point-preserving homotopic embeddings, with neither an embedded circular disc nor an embedded Möbius strip in the edges. Then there is a base point preserving isotope with a compact carrier between and . ${\displaystyle i_{0}}$ ${\displaystyle F}$ ${\displaystyle i_{0}}$ ${\displaystyle i_{1}}$

Closed area of ​​gender 2.

Homeomorphisms of surfaces

A homeomorphism is a continuous bijection with continuous inverse mapping . Two pictures

${\displaystyle H_{0},H_{1}\colon F\to F}$

are called homotop if there is a continuous figure

${\displaystyle H\colon F\times \left[0,1\right]\to F}$

with there. ${\displaystyle H(x,0)=H_{0}(x),H(x,1)=H_{1}(x)\ \forall \ x\in F}$

Two homeomorphisms are called isotopic if there is a homotopy in which the mapping for all ${\displaystyle H_{0},H_{1}}$ ${\displaystyle t\in \left[0,1\right]}$

${\displaystyle H_{t}(.)=H(.,t)\colon F\to F}$

is a homeomorphism.

Baer and Epstein used their results on curves on surfaces to prove the following equivalence of homotopy and isotopy for homeomorphisms of surfaces.

Proposition : Let be a surface with compact boundary, let ${\displaystyle F}$

${\displaystyle H_{0},H_{1}\colon F\to F}$

two homotopic homeomorphisms. (If the open or closed circular disk or the open or closed circular ring is, additionally assume that and either both are orientation-preserving or both are not orientation-preserving.) Then and are isotopic. ${\displaystyle F}$ ${\displaystyle H_{0}}$ ${\displaystyle H_{1}}$ ${\displaystyle H_{0}}$ ${\displaystyle H_{1}}$

literature

• Reinhold Baer : Isotopy of curves on orientable, closed surfaces and their connection with the topological deformation of the surfaces. In: Journal for pure and applied mathematics . Vol. 159, 1928, pp. 101-116, ( digitized version ).
• David BA Epstein : Curves on 2-manifolds and isotopies. In: Acta Mathematica . Vol. 115, 1966, pp. 83-107 ( online ).
• Andrew J. Casson , Steven A. Bleiler: Automorphisms of Surfaces after Nielsen and Thurston (= London Mathematical Society Student Texts. 9) Cambridge University Press, Cambridge et al. 1988, ISBN 0-521-34203-1 .

Web links

• Cantwell-Conlon: Hyperbolic geometry and homotopic homeomorphisms of surfaces