Casey's theorem

outer tangent sections: inner tangent sections: tangent outer sides: tangent diagonals: Casey condition:

{\ displaystyle t_ {23}, t_ {34}, t_ {24}}

{\ displaystyle t_ {12}, t_ {13}, t_ {14}}

{\ displaystyle t_ {12}, t_ {23}, t_ {34}, t_ {14}}

{\ displaystyle t_ {13}, t_ {24}}

{\ displaystyle t_ {12} t_ {34} + t_ {14} t_ {23} = t_ {13} t_ {24}}

The set of Casey is following the Irish mathematician John Casey named set of elementary geometry. It is an extension of Ptolemy's theorem and describes how the tangent sections of four circles behave in a certain configuration.

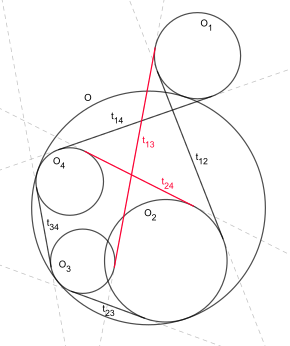
Be 4 clockwise numbered circles, all touching a fifth circle . If the circles and then both touch from the inside or both touch from the outside, then be the length of an outer tangent segment that connects the circles and . If the two circles touch from inside and outside instead , then be the length of an inner tangent segment. The following relationship now applies: ${\ displaystyle O_ {1}, O_ {2}, O_ {3}, O_ {4}}$ ${\ displaystyle O}$ ${\ displaystyle O_ {i}}$ ${\ displaystyle O_ {j}}$ ${\ displaystyle O}$ ${\ displaystyle t_ {ij}}$ ${\ displaystyle O_ {i}}$ ${\ displaystyle O_ {j}}$ ${\ displaystyle O}$ ${\ displaystyle t_ {ij}}$ ${\ displaystyle \, t_ {12} \ cdot t_ {34} + t_ {14} \ cdot t_ {23} = t_ {13} \ cdot t_ {24}}$

If the tangent sections of circles that are adjacent in the numbering are understood as "tangent outsides" (black) and the non-adjacent ones as "tangent diagonals" (red), the sentence can also be formulated as follows:

The sum of the products of the opposite tangent outsides corresponds to the product of the tangent diagonals .

The equation is known as Casey's condition . ${\ displaystyle t_ {12} \ cdot t_ {34} + t_ {14} \ cdot t_ {23} = t_ {13} \ cdot t_ {24}}$

Extensions and Applications

If the radii of the circles are allowed to approach zero, in the borderline case they go over to points on the circle and the tangent sections become the sides and diagonals of a chordal quadrilateral . So we get Ptolemy's theorem as a limiting case. ${\ displaystyle O_ {1}, O_ {2}, O_ {3}, O_ {4}}$ ${\ displaystyle O}$

Casey's theorem remains valid even if it is a degenerate circle, i.e. H. a point (radius zero) or a straight line (radius infinite). The following two sentences apply: ${\ displaystyle O}$


If 4 circles intersect at one point, the Casey condition applies : ${\ displaystyle t_ {12} \ cdot t_ {34} + t_ {14} \ cdot t_ {23} = t_ {13} \ cdot t_ {24}}$	If 4 circles have a common tangent, the Casey condition applies : ${\ displaystyle t_ {12} \ cdot t_ {34} + t_ {14} \ cdot t_ {23} = t_ {13} \ cdot t_ {24}}$

The reverse of Casey's theorem is also correct, that is, the following theorem applies:

If 4 circles fulfill the Casey condition, one of the three following cases applies:

all 4 circles have a common contact circle
all 4 circles have a common tangent
all 4 circles intersect at one point.

history

Sangaku Problem (Gunma Prefecture 1874)

The sentence was first published in Western mathematics by John Casey, but a special case of the sentence in which the 4 touching circles are also inscribed in a square was also known in Japanese mathematics of the Edo period ( Wasan ). Among other things, it has been preserved in the form of a Sangaku problem from 1874 from Gunma Prefecture and was known to the mathematician Chochu Siraishi as early as 1820 .

literature

Roger A. Johnson: Advanced Euclidean Geometry . Dover 2007, ISBN 978-0-486-46237-0 , pp. 121-127 (first published in 1929 by the Houghton Mifflin Company (Boston) under the title Modern Geometry ).
O. Bottema, Reinie Erne: Topics in Elementary Geometry . Springer 2008, ISBN 978-0-387-78130-3 , chapter The Theorems of Ptolemy and Casey .
Shay Gueron: Two Applications of the Generalized Ptolemy Theorem . The American Mathematical Monthly, Vol. 109, No. 4 (April, 2002), pp. 362-370 ( JSTOR 2695499 )

Web links

Commons : Casey's theorem - collection of pictures, videos and audio files

Eric Weisstein: Casey's Theorem . In: MathWorld (English).
Shailesh Shirali: On a generalized Ptolemy Theorem

Individual evidence

↑ Eric Weisstein: Casey's Theorem . In: MathWorld (English).
↑ Christiane Hartmann: Sangaku - Japanese Temple Geometry ( MS Word ; 3.3 MB) . (Term paper for the state examination Julius-Maximilians-Universität Würzburg 2008)

[1] Eric Weisstein: Casey's Theorem . In: MathWorld (English).

[2] Christiane Hartmann: Sangaku - Japanese Temple Geometry ( MS Word ; 3.3 MB) . (Term paper for the state examination Julius-Maximilians-Universität Würzburg 2008)