Symmetrical monoidal category

In mathematics , a symmetric monoidal category is a monoidal category (i.e., a category in which a "tensor product" is defined) whose tensor product is symmetric (i.e. one has a natural isomorphism between and for all objects and ). ${\ displaystyle \ otimes}$ ${\ displaystyle A \ otimes B}$ ${\ displaystyle B \ otimes A}$ ${\ displaystyle A}$ ${\ displaystyle B}$

A typical example is the category of vector spaces over a given body .

definition

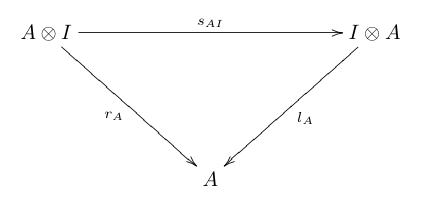
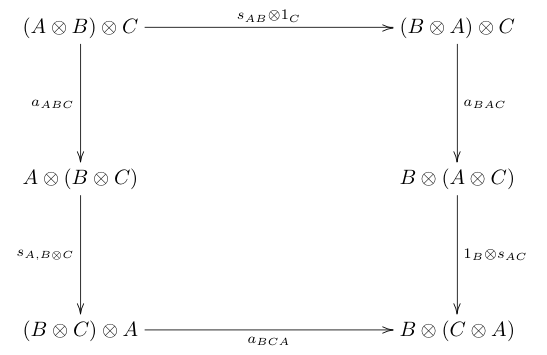
Let it be a monoidal category with associativity isomorphism and left and right unit isomorphisms, respectively . The monoidal category is called symmetric if there are two objects from an isomorphism ${\ displaystyle ({\ mathcal {C}}, \ otimes, I)}$ ${\ displaystyle a}$ ${\ displaystyle l}$ ${\ displaystyle r}$ ${\ displaystyle A, B}$ ${\ displaystyle {\ mathcal {C}}}$

{\ displaystyle s_ {AB}: A \ otimes B \ to B \ otimes A}

which is of course in and , so that the following diagrams commute : ${\ displaystyle A}$ ${\ displaystyle B}$

Compatibility with the unitary object:

Compatibility with the associative law:

Symmetric monoidal associativity coherence.png

Reverse rule:

Examples of symmetric monoidal categories

The category of sets with the set product as the tensor product and a one-element set as the unit object.

The category of topological spaces with the direct product as a tensor product and a single-element space as a unitary object.

The category of groups with the direct product as the tensor product and the trivial group as the unit object.

The category of rings with the direct product as the tensor product and the zero ring as the unit object.

The category of vector spaces over a given field with the direct sum as the tensor product and the zero vector space as the unit object.

The category of vector spaces over a given body with the tensor product of vector spaces as the tensor product and the one-dimensional space as the unit object. ${\ displaystyle K}$ ${\ displaystyle K ^ {1}}$

For a given group, the category of representations of over a given body with the tensor product of representations as the tensor product and the trivial representation as a unit object. ${\ displaystyle G}$ ${\ displaystyle G}$

Web links

symmetric monoidal category (nLab)