Triangulated category

Triangulated category is a term from homological algebra . Triangulated categories provide a common framework for derived categories and for the stable module categories of representation theory . They were originally introduced by Verdier to study derived functors of algebraic geometry .

definition

A triangulated category consists of

• an additive category , ${\displaystyle {\mathcal {C}}}$
• an additive functor which is an equivalence of categories ^(a) , and ${\displaystyle T\colon {\mathcal {C}}\rightarrow {\mathcal {C}}}$
• a class of triples of morphisms in . Elements of this class are called excellent triples . ${\displaystyle A\,{\xrightarrow {f}}\,B\,{\xrightarrow {g}}\,C\,{\xrightarrow {h}}\,T(A)}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle (f,g,h)}$

One demands that the following four axioms hold: ^(b)

(TR1)

• For each object of the triplet is excellent. ${\displaystyle X}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle X\,{\xrightarrow {\operatorname {Id} _{X}}}\,X\rightarrow \,0\,\rightarrow T(X)}$
• For every morphism from there is at least one distinctive triple of the form . ${\displaystyle A\,{\xrightarrow {f}}\,B}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle A\,{\xrightarrow {f}}\,B\,{\xrightarrow {g}}\,C\,{\xrightarrow {h}}\,T(A)}$
• A triple is excellent if and only if it is isomorphic to an excellent triple. That means: If the diagram is commutative , and if the vertical morphisms are isomorphisms , then the lower line is an excellent triple if and only if the upper line is an excellent triple.
  
  

(T2)

Is excellent, then is also excellent. ${\displaystyle A\,{\xrightarrow {f}}\,B\,{\xrightarrow {g}}\,C\,{\xrightarrow {h}}\,T(A)}$ ${\displaystyle B\,{\xrightarrow {g}}\,C\,{\xrightarrow {h}}\,T(A)\,{\xrightarrow {-T(f)}}\,T(B)}$

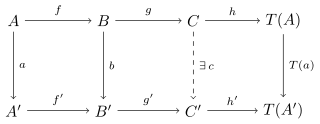
(TR3)

If the left square in the diagram commutes and the two lines are marked triples, then there is (at least) one morphism such that the whole diagram commutes.

${\displaystyle c}$

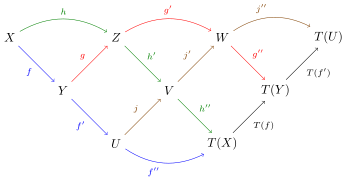
(T4) Weak octahedral axiom

Is , then there is excellent triplet , , and such that the following "Zopfdiagramm" ^(c) commutated. ${\displaystyle h=g\circ f}$ ${\displaystyle (f,f',f'')}$ ${\displaystyle (g,g',g'')}$ ${\displaystyle (h,h',h'')}$ ${\displaystyle (j,j',j'')}$

Examples

The class of the distinguished triples is often defined by describing a class of standard triples and then defining: A triple is distinguished if and only if it is isomorphic to a standard triplet.

1. Be an Abelian category . Then the category of all chain complexes is also in Abelian. Analogous to the conventional homotopy category , the homotopy category is formed by identifying chain homotopic morphisms with one another. This category is not itself Abelian, but it is triangulated, where: ${\displaystyle {\mathcal {A}}}$ ${\displaystyle \mathop {Ch} ({\mathcal {A}})}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle K({\mathcal {A}})}$ ${\displaystyle \mathop {Ch} ({\mathcal {A}})}$
   • ${\displaystyle T}$is the shift , that is, and . ${\displaystyle T(A)_{*}=A[-1]_{*}}$ ${\displaystyle T(A)_{n}=A_{n-1}}$ ${\displaystyle d_{n}^{T(A)}=-d_{n-1}^{A}}$
   • The standard triples are the triples of the shape for each morphism from , where is the mapping cone and , are the corresponding structure maps . ${\displaystyle A_{*}\,{\xrightarrow {f_{*}}}\,B_{*}\,{\xrightarrow {i_{*}}}\,C(f)_{*}\,{\xrightarrow {j_{*}}}\,A[-1]_{*}}$ ${\displaystyle A_{*}\,{\xrightarrow {f_{*}}}\,B_{*}}$ ${\displaystyle \mathop {Ch} ({\mathcal {A}})}$ ${\displaystyle C(f)_{*}}$ ${\displaystyle i_{*}}$ ${\displaystyle j_{*}}$

literature

• Sergei I. Gelfand, Yuri I. Manin : Methods of Homological Algebra . 2nd Edition. Springer, Berlin 2003, ISBN 978-3-642-07813-2 .
• Dieter Happel : Triangulated Categories in the Representation Theory of Finite Dimensional Algebras (=  London Mathematical Society Lecture Note Series . No. 119 ). Cambridge University Press, 1988, ISBN 0-521-33922-7 .
• Amnon Neeman : Triangulated Categories (=  Annals of Mathematics Studies . No. 146 ). Princeton University Press, 2001, ISBN 0-691-08685-0 .
• Wolfgang Soergel : Derived Categories and Functors. (PDF) Mathematical Institute, University of Freiburg, April 7, 2017, accessed on April 8, 2017 (lecture notes). 
• Charles A. Weibel : An introduction to homological algebra (=  Cambridge Studies in Advanced Mathematics . No. 38 ). Cambridge University Press, 1994, ISBN 0-521-43500-5 , chapter 10 .
• Alexander Zimmermann: Representation Theory: A Homological Algebra Point of View (=  Algebra and Applications . No. 19 ). Springer, Cham 2014, ISBN 978-3-319-07968-4 , §3.4 .

Remarks

^(a)Many sources even require an isomorphism of categories, which simplifies some statements. The stable module category is an example where - in this case the Heller operator - is not an isomorphism of categories. ${\displaystyle T}$

^(b)Axioms after Paul Balmers' review of an article by J. Peter May

^(c)This diagrammatic representation of the axiom of the octahedron is by May, who cites a sine wave diagram by JF Adams as his inspiration.

Individual evidence

1. ↑ Alexander Zimmermann: Representation Theory: A Homological Algebra Point of View (=  Algebra and Applications . No. 19 ). Springer, Cham 2014, ISBN 978-3-319-07967-7 , p. 288 , doi : 10.1007 / 978-3-319-07968-4 .
2. ↑ Paul Balmer : MR1867203 (2002k: 18019). In: MathSciNet . American Mathematical Society , accessed April 26, 2017 (credit required). 
3. ↑ ^{a b} J. Peter May : The additivity of traces in triangulated categories . In: Advances in Mathematics . tape 163 , no. 1 , October 15, 2001, p. 34-73 , doi : 10.1006 / aima.2001.1995 .
4. ^ JF Adams : Stable Homotopy and Generalized Homology . University of Chicago Press, Chicago 1974, ISBN 0-226-00523-2 , pp. 212 .