Multi-pendulum

A multi- pendulum is a pendulum with additional pendulums attached to its arm. An unpredictable movement pattern is created, which varies greatly even with minor disturbances. Chaotic processes can be simulated easily, which is why it has become a popular model in chaos theory .

Model presentation

The model of the multi-pendulum -th stage is an idealized system of a thread pendulum, to whose oscillating mass point further thread pendulums of the same construction are coupled. The connecting threads between the suspension point and the mass points are regarded as completely inelastic, massless rods. The entire system is considered to be frictionless. ${\displaystyle n}$ ${\displaystyle n-1}$

Equations of motion of the n- th order multiple pendulum

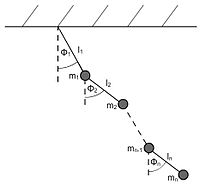
Structure: multi-pendulum

The equations of motion for a multipendulum- th level can be derived with the Lagrange formalism of the second kind. ${\displaystyle n}$

Generalized coordinates

Using trigonometry one obtains:

${\displaystyle x_{1}=l_{1}\sin \varphi _{1}}$

${\displaystyle y_{1}=-l_{1}\cos \varphi _{1}}$

${\displaystyle x_{2}=l_{1}\sin \varphi _{1}+l_{2}\sin \varphi _{2}}$

${\displaystyle y_{2}=-l_{1}\cos \varphi _{1}-l_{2}\cos \varphi _{2}}$

...

${\displaystyle x_{n}=l_{1}\sin \varphi _{1}+...+l_{n}\sin \varphi _{n}}$

${\displaystyle y_{n}=-l_{1}\cos \varphi _{1}-...-l_{n}\cos \varphi _{n}}$

Consequently, the Cartesian coordinates of the mass points for ∈ {1, ..., } and their time derivatives can be written in the following form: ${\displaystyle (x_{k}|y_{k})}$ ${\displaystyle m_{k}}$ ${\displaystyle k}$ ${\displaystyle n}$

${\displaystyle x_{k}=\sum _{i=1}^{k}l_{i}\sin \varphi _{i}}$

${\displaystyle {\dot {x}}_{k}=\sum _{i=1}^{k}l_{i}{\dot {\varphi }}_{i}\cos \varphi _{i}}$

${\displaystyle y_{k}=-\sum _{i=1}^{k}l_{i}\cos \varphi _{i}}$

${\displaystyle {\dot {y}}_{k}=\sum _{i=1}^{k}l_{i}{\dot {\varphi }}_{i}\sin \varphi _{i}}$

Lagrange function

Kinetic energy and potential result in: ${\displaystyle T}$ ${\displaystyle V}$

${\displaystyle T(\varphi _{1},...,\varphi _{n},{\dot {\varphi }}_{1},...,{\dot {\varphi }}_{n})=\sum _{k=1}^{n}{\frac {m_{k}}{2}}({\dot {x}}_{k}^{2}+{\dot {y}}_{k}^{2})}$

${\displaystyle V(\varphi _{1},...,\varphi _{n})=g\sum _{k=1}^{n}m_{k}y_{k}}$

Thus the Lagrange function is : ${\displaystyle L=T-V}$

${\displaystyle L(\varphi _{1},...,\varphi _{n},{\dot {\varphi }}_{1},...,{\dot {\varphi }}_{n})={\frac {1}{2}}\sum _{k=1}^{n}m_{k}\left[\left(\sum _{i=1}^{k}l_{i}{\dot {\varphi }}_{i}\cos \varphi _{i}\right)^{2}+\left(\sum _{i=1}^{k}l_{i}{\dot {\varphi }}_{i}\sin \varphi _{i}\right)^{2}\right]+g\sum _{k=1}^{n}\sum _{i=1}^{k}m_{k}l_{i}\cos \varphi _{i}}$

Equations of motion

The equations of motion of the n- th level multiple pendulum result from

${\displaystyle {d \over dt}{\partial {L} \over \partial {{\dot {\varphi }}_{j}}}-{\partial {L} \over \partial {\varphi _{j}}}=0}$

or.

${\displaystyle {d \over dt}{\partial {T} \over \partial {{\dot {\varphi }}_{j}}}-{\partial {} \over \partial {\varphi _{j}}}(T-V)=0}$

for ∈ {1, ..., }. ${\displaystyle j}$ ${\displaystyle n}$

The equations of motion for the generalized coordinates ( ) represent a nonlinear system of differential equations of the second order, which cannot be solved analytically. ${\displaystyle {\varphi _{1}},...,{\varphi _{n}}}$ ${\displaystyle n}$ ${\displaystyle n>1}$

It can in known adverse conditions, such as the start values ${\displaystyle 2n}$

${\displaystyle \left(\varphi _{1}(t=0),...,\varphi _{n}(t=0),{\dot {\varphi }}_{1}(t=0),...,{\dot {\varphi }}_{n}(t=0)\right)}$

can be solved using numerical methods . Small-angle approximations can be made to simplify the equations of motion .

Chaotic movement patterns arise for steps . Even slight changes in the local coordinates and / or their temporal derivatives lead to significant changes in the further course of movement. ${\displaystyle n>1}$

Equations of motion for one- to three-stage pendulums

Mathematical pendulum

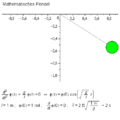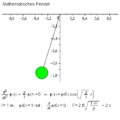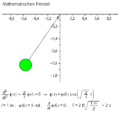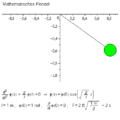
For the simple case of the mathematical pendulum results . ${\displaystyle n=1}$

Here kinetic energy yield and potential to ${\displaystyle T}$ ${\displaystyle V}$

${\displaystyle T(\varphi ,{\dot {\varphi }})={\frac {m}{2}}l^{2}{\dot {\varphi }}^{2}}$

${\displaystyle V(\varphi )=-mgl\cos \varphi }$

with . ${\displaystyle m:=m_{1},l:=l_{1},\varphi :=\varphi _{1}}$

Accordingly, the equation of motion is:

${\displaystyle {\ddot {\varphi }}+{\frac {g}{l}}\sin \varphi =0}$

The equation can be simplified with the small-angle approximation : ${\displaystyle \sin \varphi \approx \varphi }$

${\displaystyle {\ddot {\varphi }}+{\frac {g}{l}}\varphi =0}$

A useful solution to the equation of motion is

${\displaystyle \varphi (t)=\varphi (0)\cos \left({\sqrt {\frac {g}{l}}}t+\alpha \right)}$,

so that if the start conditions are known for the parameter : ${\displaystyle \alpha }$

${\displaystyle \alpha =\arcsin \left(-{\frac {{\dot {\varphi }}(0)}{\varphi (0)}}{\sqrt {\frac {l}{g}}}\right)}$

The pendulum swings in harmony with the period:

${\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}}$

Double pendulum

The case represents the double pendulum . ${\displaystyle n=2}$

Here kinetic energy and potential result as: ${\displaystyle T}$ ${\displaystyle V}$

${\displaystyle T(\varphi _{1},\varphi _{2},{\dot {\varphi }}_{1},{\dot {\varphi }}_{2})={\frac {m_{1}}{2}}l_{1}^{2}{\dot {\varphi }}_{1}^{2}+{\frac {m_{2}}{2}}\left(l_{1}^{2}{\dot {\varphi }}_{1}^{2}+l_{2}^{2}{\dot {\varphi }}_{2}^{2}+2l_{1}l_{2}{\dot {\varphi }}_{1}{\dot {\varphi }}_{2}\cos(\varphi _{1}-\varphi _{2})\right)}$

${\displaystyle V(\varphi _{1},\varphi _{2})=-(m_{1}+m_{2})gl_{1}\cos \varphi _{1}-m_{2}gl_{2}\cos \varphi _{2}}$

The equations of motion are accordingly:

${\displaystyle m_{2}l_{2}{\ddot {\varphi }}_{2}\cos \left(\varphi _{1}-\varphi _{2}\right)+\left(m_{1}+m_{2}\right)l_{1}{\ddot {\varphi }}_{1}+m_{2}l_{2}{\dot {\varphi }}_{2}^{2}\sin \left(\varphi _{1}-\varphi _{2}\right)+\left(m_{1}+m_{2}\right)g\sin \varphi _{1}=0}$

and

${\displaystyle l_{2}{\ddot {\varphi }}_{2}+l_{1}{\ddot {\varphi }}_{1}\cos \left(\varphi _{1}-\varphi _{2}\right)-l_{1}{\dot {\varphi }}_{1}^{2}\sin \left(\varphi _{1}-\varphi _{2}\right)+g\sin \varphi _{2}=0}$

An example of a double pendulum is a bell with a clapper.

Triple pendulum

The case represents the triple pendulum . ${\displaystyle n=3}$

Here the kinetic energy results from: ${\displaystyle T}$

${\displaystyle T(\varphi _{1},\varphi _{2},\varphi _{3},{\dot {\varphi }}_{1},{\dot {\varphi }}_{2},{\dot {\varphi }}_{3})={\frac {m_{1}+m_{2}+m_{3}}{2}}l_{1}^{2}{\dot {\varphi }}_{1}^{2}+{\frac {m_{2}+m_{3}}{2}}l_{2}^{2}{\dot {\varphi }}_{2}^{2}+{\frac {m_{3}}{2}}l_{3}^{2}{\dot {\varphi }}_{3}^{2}+(m_{2}+m_{3})l_{1}l_{2}{\dot {\varphi }}_{1}{\dot {\varphi }}_{2}\cos(\varphi _{1}-\varphi _{2})}$

${\displaystyle +m_{3}l_{1}l_{3}{\dot {\varphi }}_{1}{\dot {\varphi }}_{3}\cos(\varphi _{1}-\varphi _{3})+m_{3}l_{2}l_{3}{\dot {\varphi }}_{2}{\dot {\varphi }}_{3}\cos(\varphi _{2}-\varphi _{3})}$

The following applies to the potential : ${\displaystyle V}$

${\displaystyle V(\varphi _{1},\varphi _{2},\varphi _{3})=-(m_{1}+m_{2}+m_{3})gl_{1}\cos \varphi _{1}-(m_{2}+m_{3})gl_{2}\cos \varphi _{2}-m_{3}gl_{3}\cos \varphi _{3}}$

The equations of motion are accordingly:

${\displaystyle m_{3}l_{3}{\ddot {\varphi }}_{3}\cos(\varphi _{1}-\varphi _{3})+(m_{2}+m_{3})l_{2}{\ddot {\varphi }}_{2}\cos(\varphi _{1}-\varphi _{2})+(m_{1}+m_{2}+m_{3})l_{1}{\ddot {\varphi }}_{1}+m_{3}l_{3}{\dot {\varphi }}_{3}^{2}\sin(\varphi _{1}-\varphi _{3})}$

${\displaystyle +(m_{2}+m_{3})l_{2}{\dot {\varphi }}_{2}^{2}\sin(\varphi _{1}-\varphi _{2})+(m_{1}+m_{2}+m_{3})g\sin \varphi _{1}=0}$

and

${\displaystyle m_{3}l_{3}{\ddot {\varphi }}_{3}\cos(\varphi _{2}-\varphi _{3})+(m_{2}+m_{3})l_{2}{\ddot {\varphi }}_{2}+(m_{2}+m_{3})l_{1}{\ddot {\varphi }}_{1}\cos(\varphi _{1}-\varphi _{2})-(m_{2}+m_{3})l_{1}{\dot {\varphi }}_{1}^{2}\sin(\varphi _{1}-\varphi _{2})}$

${\displaystyle +m_{3}l_{3}{\dot {\varphi }}_{3}^{2}\sin(\varphi _{2}-\varphi _{3})+(m_{2}+m_{3})g\sin \varphi _{2}=0}$

and

${\displaystyle l_{3}{\ddot {\varphi }}_{3}+l_{2}{\ddot {\varphi }}_{2}\cos(\varphi _{2}-\varphi _{3})+l_{1}{\ddot {\varphi }}_{1}\cos(\varphi _{1}-\varphi _{3})-l_{2}{\dot {\varphi }}_{2}^{2}\sin(\varphi _{2}-\varphi _{3})-l_{1}{\dot {\varphi }}_{1}^{2}\sin(\varphi _{1}-\varphi _{3})+g\sin \varphi _{3}=0}$

Simulation of the trajectories

• 

  Simulation: ${\displaystyle n=1}$

• 

  Simulation: ${\displaystyle n=2}$

• 

  Simulation: ${\displaystyle n=3}$

literature

• Georg Hamel: Theoretical Mechanics . Springer, Berlin 1967. Corrected reprint 1978, ISBN 3-540-03816-7
• Friedhelm Kuypers: Classic mechanics . 5th edition. VCH, Weinheim 1997, ISBN 3-527-29269-1
• Landau / Lifschitz: Textbook of theoretical physics. Volume 1: Mechanics . 14th edition. German, Thun 1997, ISBN 3-8171-1326-9

swell

• LD Landau, EM Lifschitz: Volume 1 of Course of Theoretical Physics . 3rd Edition 1976, ISBN 0-7506-2896-0 , §5, p. 11 f. (English)
• Derivation of the differential equations to describe the double pendulum (English)

Web links

• Simulations of multiple pendulums
• Double pendulum simulation in Java and Python (German)