Vector control
The vector control is a control concept in which sinusoidal - or assumed to be largely sinusoidal - alternating variables (e.g. alternating voltages and alternating currents) are not controlled directly in their instantaneous value, but in an instantaneous value adjusted for the phase angle within the period. For this purpose, the recorded alternating variables are each transferred to a coordinate system rotating with the frequency of the alternating variables. Within the rotating coordinate system, the alternating variables then result in constant variables to which all common methods of control engineering can be applied.
General
For practical reasons, one with two mutually perpendicular axes d and q is practically always chosen for the rotating coordinate system when controlling electrical quantities. This has the advantage that the space vector representation ( English space vector ) of AC voltages and currents and their relation is identical to each other, resulting in the corresponding models of electric motors can be used directly.
With this vector control, which is also called field-oriented control with reference to the rotating field of an electrical machine , a frequency converter for electric motors achieves increased speed and positioning accuracy compared to a control that only uses a low-pass filter for effective values of currents and voltages of one or even several periods (n) used.
The use of vector control is not limited to drives, the principle can also be used for converters for feeding into networks. The frequency and phase can either be specified by the network, they are then measured, as is the case with drive control, or the converter gives, e.g. B. in an island network , these sizes before.
The vector control reaches the limit of its applicability when the variables to be controlled and measured are no longer sufficiently sinusoidal. In this case, the transfer to the rotating coordinate system can only eliminate the influence of the fundamental oscillation, the harmonics remain and cannot be distinguished by the controller from exposure to disturbance variables . However, filtering the harmonics is usually sufficient for practical applications in drive technology. In applications for converters that do not act on mechanical drives or are not supported by them, but z. If, for example, you work directly on other power converters (e.g. battery power converters in island operation supplies 230 V ~ compact fluorescent lamps ), this must be taken into account.
Vector control for synchronous machines
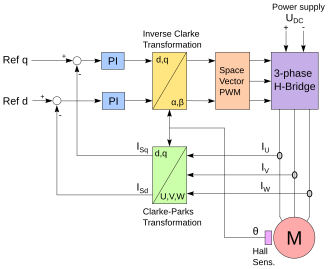
If the stator flux and stator current are parallel in the rotating DQ field in the synchronous motor, the torque is zero. The rotor-related d / q system is calculated from the stator-related three-phase system using the Clarke transformation and subsequent d / q transformation (Park transformation) . The d and q vectors are perpendicular to each other, the q value represents the torque and the d value the magnetic flux density and can be modeled similar to a DC machine with a PI controller . The torque of the machine can be influenced by externally specified q reference value. In the case of synchronous motors permanently excited in the rotor, which is typical for so-called brushless direct current motors (BLDC), the d reference value in the basic speed range is zero, provided that the d and q inductances are of the same size, i.e. there is no reluctance contribution to the torque. In the field weakening range, a negative d reference value is used to limit the induced voltage. With an inverse transformation and subsequent space vector modulation ( English Space Vector PWM ), the drive signals for the three phases performed four-quadrant formed.
To regulate the space vector at right angles , a control loop with feedback to the machine is required, which specifies the position of the pole wheel . In synchronous machines , this feedback was usually implemented with three Hall sensors . However, since these are prone to errors and only offer a low angular resolution, encoders ( resolvers , optical incremental and absolute encoders or inductive encoders) are mostly used in servo drives . With block commutation, sensorless controls can be implemented by measuring back the counter voltage induced in the motor . However, this feedback has increasing disadvantages, especially at low speeds. Another sensorless method for detecting the rotor position at low speeds is to measure the winding inductances. These change depending on whether there is a permanent magnet over the measured coil or not.
Another possibility to operate a synchronous machine sensorless using vector control is based on mathematical calculation of the required control parameters. The decisive factor here is a realistic and as precise as possible software model of the machine. A digital signal processor uses this machine model to estimate the parameters required for vector control, such as the rotor angle and the speed . The only measured variables required with this method are the three stator currents of the machine. Since the star point of the machine (if present) is usually not connected, it is sufficient to measure two stator currents, which inevitably allows conclusions to be drawn about the third stator current.
Vector control for asynchronous machines
The vector control of rotating field machines was invented in 1968 by K. Hasse at the TH Darmstadt and independently of it also described in the doctoral thesis of Felix Blaschke 1973 at the TU Braunschweig with the title "The method of field orientation for the control of the rotating field machine". With the vector control of the asynchronous machine, the magnetic air gap field is decisive for the operating behavior. In the case of the basic speed range, the magnetizing current must be kept constant regardless of the speed.
Asynchronous machines can also be controlled with a vector-modulated frequency to increase performance. The active and reactive currents Iw and Iu are of interest here. The reactive current ensures magnetization of the stator, the active current for the torque. Since the reactance X of the stator changes with the frequency, but the ohmic resistance R remains constant when the frequency changes, the U / f characteristic curve in an asynchronous motor is non-linear. Especially at low frequencies, the voltage drop across R is so great that no full reactive current can flow through X and the machine then loses torque due to insufficient magnetization. This is also the reason why it is difficult to regulate very low speeds with asynchronous machines and why the asynchronous motor is unsuitable for precise positioning.
In order to compensate for these disadvantages at low speeds, many frequency converters , which work according to the U / f characteristic , offer a "boost" mode for low speeds, in which the voltage drop across the stator R is additionally fed in. However, such fixed boost factors are only a compromise for an average torque output, since the torque also causes an active current. This active current results in the same voltage drop in the equivalent circuit diagram of the stator R, which is why the desired reactive current is again not optimal. In the event of a faulty reactive current, either the torque is too low or the machine has to convert a high iron loss into heat if it is over-magnetized. In addition, the effective resistance R of the machine changes when it is heated to a value that can no longer be neglected, especially at low speeds.
At this point, the vector modulation intervenes and tracks the rotating field vector in a closed control loop, which ideally takes into account all of the system's disturbances. In practice, almost ideal servo properties can be achieved with asynchronous machines for positioning down to zero speed. With various frequency converters it is now state of the art that the control of the vector modulation works adaptively. Unknown machine models are learned and application-specific load jumps are automatically adjusted.
Web links
- Study work, presentation and animations introducing the topic of space vector
- Application example and theory of field-oriented control with a sensor from Atmel (PDF; 467 kB)
- Application example and theory of field-oriented control without a sensor from Microchip (PDF; 486 kB)
- Position detection and start-up algorithm of a rotor in a sensorless BLDC motor utilizing induction variation PREM (PDF; 1256 kB)
- Dissertation (PDF; 2.1 MB) on the field-oriented control of the permanent magnet synchronous machine