Kac-Moody algebra

Kac-Moody algebras , named after Victor Kac and Robert Moody , are algebras studied in the mathematical theory of Lie algebras. One starts with a matrix with certain properties and applies a method to it that is based on the classical construction of a finite-dimensional, semi-simple Lie algebra from a given Cartan matrix . One can then identify three types of such Kac-Moody algebras. The finite-type algebras (see below) are the finite-dimensional semi-simple Lie algebras known from classical theory, so that the theory of Kac-Moody algebras can be viewed as a generalization of classical theory. There are also two further types, the affine type and the indefinite type (see below), which are neither finite-dimensional nor semi-simple.

construction

Generalized Cartan matrices

A matrix is called a generalized Cartan matrix , if ${\displaystyle n\times n}$ ${\displaystyle A=(A_{i,j})}$

• All coefficients are integral, that is, for all ${\displaystyle A_{i,j}\in \mathbb {Z} }$ ${\displaystyle i,j=1,\ldots ,n}$
• ${\displaystyle A_{i,i}=2}$ for all ${\displaystyle i=1,\ldots ,n}$
• ${\displaystyle A_{i,j}\leq 0}$ for all ${\displaystyle i,j=1,\ldots ,n,\,i\not =j}$
• From always follows for everyone . ${\displaystyle A_{i,j}=0}$ ${\displaystyle A_{j,i}=0}$ ${\displaystyle i,j=1,\ldots ,n}$

Obviously, Cartan matrices are examples of generalized Cartan matrices.

Two generalized cartan matrices and are called equivalent if there is a permutation on with . ${\displaystyle n\times n}$ ${\displaystyle A=(A_{i,j})}$ ${\displaystyle A'=(A'_{i,j})}$ ${\displaystyle \sigma }$ ${\displaystyle \{1,\ldots ,n\}}$ ${\displaystyle A'_{i,j}=A_{\sigma (i),\sigma (j)}}$

A generalized Cartan matrix is ​​called decomposable if it becomes a matrix of form

${\displaystyle {\begin{pmatrix}A_{1}&0\\0&A_{2}\end{pmatrix}}}$

with sub-matrices and is equivalent, otherwise indivisible . ${\displaystyle A_{1}}$ ${\displaystyle A_{2}}$

Realizations of a matrix

For a given generalized cartan matrix there is ${\displaystyle n\times n}$ ${\displaystyle A=(A_{i,j})}$

• a finite - vector space ${\displaystyle \mathbb {C} }$ ${\displaystyle H}$
• a linearly independent subset , ${\displaystyle \Pi ^{\vee }=\{h_{1},\ldots ,h_{n}\}\subset H}$
• a linearly independent subset , where the dual space of is, ${\displaystyle \Pi =\{\alpha _{1},\ldots ,\alpha _{n}\}\subset H^{*}}$ ${\displaystyle H^{*}}$ ${\displaystyle H}$

so that for everyone ${\displaystyle A_{i,j}=\alpha _{j}(h_{i})}$ ${\displaystyle i,j=1,\ldots ,n}$

The data is called a realization of . It can be shown that the dimension of at least , wherein the rank of the matrix is that this minimum is attained, and that for any two realizations and a minimum dimension Vektorraumisomorphismus is, the on maps and the dual picture on maps. These so-called minimal realizations are thus clearly defined except for isomorphism. ${\displaystyle (H,\Pi ^{\vee },\Pi )}$ ${\displaystyle A}$ ${\displaystyle H}$ ${\displaystyle 2n-\mathrm {rang} (A)}$ ${\displaystyle \mathrm {rang} (A)}$ ${\displaystyle (H_{1},\Pi _{1}^{\vee },\Pi _{1})}$ ${\displaystyle (H_{2},\Pi _{2}^{\vee },\Pi _{2})}$ ${\displaystyle \varphi :H_{1}\rightarrow H_{2}}$ ${\displaystyle \Pi _{1}^{\vee }}$ ${\displaystyle \Pi _{2}^{\vee }}$ ${\displaystyle \Pi _{2}}$ ${\displaystyle \Pi _{1}}$

A Lie algebra from generators and relations

So far we have constructed a minimal implementation for a generalized cartan matrix . We use this data to define a Lie algebra from generators and relations . The set of producers is ${\displaystyle n\times n}$ ${\displaystyle A=(A_{i,j})}$ ${\displaystyle (H,\Pi ^{\vee }=\{h_{1},\ldots ,h_{n}\},\Pi =\{\alpha _{1},\ldots ,\alpha _{n}\})}$ ${\displaystyle {\tilde {L}}(A)}$

${\displaystyle X=\{e_{1},\ldots ,e_{n},f_{1},\ldots ,f_{n}\}\cup \{{\tilde {x}}\mid x\in H\}}$.

The elements are only symbols, only the matrix size and the vector space are included here. The relations are ${\displaystyle n}$ ${\displaystyle H}$

• ${\displaystyle {\tilde {x}}-\lambda {\tilde {y}}-\mu {\tilde {z}}}$   for everyone   with ${\displaystyle x,y,z\in H,\,\lambda ,\mu \in \mathbb {C} }$ ${\displaystyle x=\lambda x+\mu z}$
• ${\displaystyle [{\tilde {x}}{\tilde {y}}]}$   for all   ${\displaystyle x,y\in H}$
• ${\displaystyle [e_{i}f_{i}]-{\tilde {h_{i}}}}$   for all   ${\displaystyle i=1,\ldots ,n}$
• ${\displaystyle [e_{i}f_{j}]}$   for all   ${\displaystyle i,j=1,\ldots ,n,\,i\not =j}$
• ${\displaystyle [{\tilde {x}}e_{i}]-\alpha _{i}(x)}$   for all   ${\displaystyle i=1,\ldots ,n,\,x\in H}$
• ${\displaystyle [{\tilde {x}}f_{i}]+\alpha _{i}(x)}$   for all   ${\displaystyle i=1,\ldots ,n,\,x\in H}$

If we denote the set of these relations, we put ${\displaystyle R}$

${\displaystyle {\tilde {L}}(A):=L(X;R)}$, where the latter is the Lie algebra defined by the generators and relations . ${\displaystyle X}$ ${\displaystyle R}$

The first two groups of relations obviously lead to a Lie-algebra homomorphism between Abelian Lie-algebras . One can even show that this is an isomorphism . ${\displaystyle H\mapsto {\tilde {H}}:=\{{\tilde {x}}\mid x\in H\},\,x\mapsto {\tilde {x}}}$

Definition of the Kac-Moody algebras

For a generalized Cartan matrix , we have constructed a Lie algebra with an Abelian subalgebra contained in it . It can now be shown that ${\displaystyle A=(A_{i,j})}$ ${\displaystyle {\tilde {L}}(A)}$ ${\displaystyle {\tilde {H}}}$

${\displaystyle I:=\sum \{J\mid \,J\subset {\tilde {L}}(A){\text{ Lie-Ideal mit }}J\cap {\tilde {H}}=\{0\}\}}$

is again an ideal with . Is called ${\displaystyle I\cap {\tilde {H}}=\{0\}}$

${\displaystyle L(A):={\tilde {L}}(A)/I}$

the Kac-Moody algebra for the generalized Cartan matrix . ${\displaystyle A}$

One can show that the isomorphism class only depends on the equivalence class of the generalized Cartan matrix, in particular not on the choice of a minimal realization. If there is even a Cartan matrix, then the Kac-Moody algebra is too isomorphic to the finite-dimensional semi-simple Lie algebra with this Cartan matrix. ${\displaystyle L(A)}$ ${\displaystyle A}$ ${\displaystyle A}$

Three types of Kac-Moody algebras

The Kac-Moody algebras on indecomposable generalized Cartan matrices fall into three types. They are defined by properties of the underlying generalized Cartan matrix. Note that such matrices have integer and thus real-valued coefficients and therefore operate on the , the vector space of the column vectors. On the is component-wise order given, that is , if component by component applies. We write accordingly if applies to components . ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \leq }$ ${\displaystyle u\leq v}$ ${\displaystyle u_{i}\leq v_{i}}$ ${\displaystyle u<v}$ ${\displaystyle u_{i}<v_{i}}$

The following type designations are used, for which there is an indecomposable generalized Cartan matrix, both for and for the Kac-Moody algebra . ${\displaystyle A}$ ${\displaystyle n\times n}$ ${\displaystyle A}$ ${\displaystyle L(A)}$

Kac-Moody algebras of finite type

${\displaystyle A}$and thus also has finite type, if ${\displaystyle L(A)}$

• ${\displaystyle \det(A)\not =0}$,
• There is with and , ${\displaystyle u\in \mathbb {R} ^{n}}$ ${\displaystyle u>0}$ ${\displaystyle Au>0}$
• From follows or . ${\displaystyle Au\geq 0}$ ${\displaystyle u>0}$ ${\displaystyle u=0}$

Affine type Kac-Moody algebras

${\displaystyle A}$and thus also has affine type, if ${\displaystyle L(A)}$

• ${\displaystyle \mathrm {rang} (A)=n-1}$, that means the Korang is 1,
• There is with and , ${\displaystyle u\in \mathbb {R} ^{n}}$ ${\displaystyle u>0}$ ${\displaystyle Au=0}$
• From follows . ${\displaystyle Au\geq 0}$ ${\displaystyle Au=0}$

Kac-Moody algebras of indefinite type

${\displaystyle A}$and thus also has indefinite type, if ${\displaystyle L(A)}$

• There is with and , ${\displaystyle u\in \mathbb {R} ^{n}}$ ${\displaystyle u>0}$ ${\displaystyle Au<0}$
• Out and follows . ${\displaystyle Au\geq 0}$ ${\displaystyle u\geq 0}$ ${\displaystyle u=0}$

Remarks

It is not obvious that this is actually a tripartite division of the indecomposable generalized Cartan matrices. Alternatively, one can characterize these three types for indecomposable generalized Cartan matrices as follows:

• ${\displaystyle A}$has finite type if and only if there is with and ${\displaystyle u\in \mathbb {R} ^{n}}$ ${\displaystyle u>0}$ ${\displaystyle Au>0}$
• ${\displaystyle A}$has affine type if and only if there is with and ${\displaystyle u\in \mathbb {R} ^{n}}$ ${\displaystyle u>0}$ ${\displaystyle Au=0}$
• ${\displaystyle A}$has indefinite type if and only if there is with and ${\displaystyle u\in \mathbb {R} ^{n}}$ ${\displaystyle u>0}$ ${\displaystyle Au<0}$

One can show that Kac-Moody algebras of finite type are precisely the finite-dimensional simple Lie algebras . The Kac-Moody algebras of affine or indefinite type are neither semi-simple, they have a non-trivial center , nor are they finite-dimensional.

Dynkin diagrams

Similar to the theory of finite-dimensional semi-simple Lie algebras, one can assign a Dynkin diagram to every generalized Cartan matrix , this happens according to the following rules: The Dynkin diagram for the generalized Cartan matrix is a graph made up of nodes , which are marked with. For the edges between these nodes, proceed as follows: ${\displaystyle n\times n}$ ${\displaystyle A=(A_{i,j})}$ ${\displaystyle n}$ ${\displaystyle 1,\ldots ,n}$

• If the nodes and are not connected. ${\displaystyle A_{i,j}A_{j,i}=0}$ ${\displaystyle i}$ ${\displaystyle j}$
• If , the nodes and are connected by a single edge. ${\displaystyle A_{i,j}A_{j,i}=1}$ ${\displaystyle i}$ ${\displaystyle j}$
• If the nodes and are connected by two edges. A> sign through these edges indicates with the tip , if , otherwise after . ${\displaystyle A_{i,j}A_{j,i}=2}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle i}$ ${\displaystyle A_{i,j}=-2}$ ${\displaystyle j}$
• Is , the nodes and are connected by three edges. A> sign through these edges indicates with the tip , if , otherwise after . ${\displaystyle A_{i,j}A_{j,i}=3}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle i}$ ${\displaystyle A_{i,j}=-3}$ ${\displaystyle j}$
• If and , the nodes and are connected by four edges. A> sign through these edges indicates with the tip , if , otherwise after . ${\displaystyle A_{i,j}A_{j,i}=4}$ ${\displaystyle |A_{i,j}|\not =|A_{j,i}|}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle i}$ ${\displaystyle A_{i,j}=-4}$ ${\displaystyle j}$
• If and , the nodes and are connected by two edges. A> and a <sign are drawn through these edges, their tips point to one another. ${\displaystyle A_{i,j}A_{j,i}=4}$ ${\displaystyle A_{i,j}=A_{j,i}=-2}$ ${\displaystyle i}$ ${\displaystyle j}$
• If , the nodes and are connected by a single edge and the whole numbers and are noted on this edge. ${\displaystyle A_{i,j}A_{j,i}\geq 5}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle |A_{i,j}|}$ ${\displaystyle |A_{j,i}|}$

It is clear that you can recover from the Dynkin diagram, the generalized Cartan matrix, as well, that a generalized Cartan matrix if and indivisible if their Dynkin diagram coherently is.

In classical theory, that is, for indecomposable generalized Cartan matrices of finite type, one obtains the well-known list of Dynkin diagrams , which represents a complete classification of the finite-dimensional simple Lie algebras. For indecomposable generalized Cartan matrices of affine type, a complete classification is also possible, here too a manageable list is obtained. The last-mentioned rule for creating the Dynkin diagram does not apply in the affine case; this only occurs in the case of indecomposable generalized Cartan matrices of indefinite type. ${\displaystyle A_{n},B_{n},C_{n},D_{n},E_{6},E_{7},E_{8},F_{4},G_{2}}$

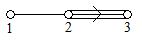
The Dynkin diagram for the generalized Cartan matrix ${\displaystyle {\tilde {G}}_{2}}$

As an example of a generalized Cartan matrix of affine type, consider

${\displaystyle {\tilde {G}}_{2}={\begin{pmatrix}2&-1&0\\-1&2&-1\\0&-3&2\end{pmatrix}}}$.

The name comes from a classification of the indecomposable Cartan matrices of affine type. There ${\displaystyle {\tilde {G}}_{2}}$

${\displaystyle {\begin{pmatrix}2&-1&0\\-1&2&-1\\0&-3&2\end{pmatrix}}\cdot {\begin{pmatrix}1\\2\\3\end{pmatrix}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}}$,

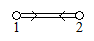
The Dynkin diagram for the generalized Cartan matrix ${\displaystyle {\tilde {A}}_{1}}$

if, according to the above criteria, there is actually an affine type: There is a with . The associated Dynkin diagram is shown in the adjacent drawing. ${\displaystyle u>0}$ ${\displaystyle {\tilde {G}}_{2}u=0}$

Another example of a generalized affine type Cartan matrix is

${\displaystyle {\tilde {A}}_{1}={\begin{pmatrix}2&-2\\-2&2\end{pmatrix}}}$.

The penultimate rule is used to create the Dynkin diagram.

Here is the complete list of all Dynkin diagrams for indecomposable, generalized Cartan matrices of affine type:

The names given for the Dynkin diagrams are standard names. The tilde used indicates a certain affinization , i.e. a process with which one can generate more from given Lie algebras. The linked to these Dynkin diagrams Kac-Moody algebras are called exactly that is, we speak of Kac-Moody algebras , , , , , , , , , , , , , , . ${\displaystyle {\tilde {A}}_{1}'}$ ${\displaystyle {\tilde {A}}_{n}}$ ${\displaystyle {\tilde {B}}_{n}}$ ${\displaystyle {\tilde {B}}_{n}^{t}}$ ${\displaystyle {\tilde {C}}_{n}}$ ${\displaystyle {\tilde {C}}_{n}^{t}}$ ${\displaystyle {\tilde {C}}_{n}'}$ ${\displaystyle {\tilde {D}}_{n}}$ ${\displaystyle {\tilde {E}}_{6}}$ ${\displaystyle {\tilde {E}}_{7}}$ ${\displaystyle {\tilde {E}}_{8}}$ ${\displaystyle {\tilde {F}}_{4}}$ ${\displaystyle {\tilde {F}}_{4}^{t}}$ ${\displaystyle {\tilde {G}}_{2}}$ ${\displaystyle {\tilde {G}}_{2}^{t}}$

further remarks

For Kac-Moody algebras, large parts of the root system- based theory of finite-dimensional semi-simple Lie algebras can be set up analogously. The image of in quotient algebra serves as a substitute for the Cartan sub-algebra . It can be shown that the mapping is injective. So one can understand it as a sub- algebra of. This is a representation of the form ${\displaystyle {\tilde {H}}}$ ${\displaystyle L(A)}$ ${\displaystyle H\rightarrow L(A),\,x\mapsto {\tilde {x}}+I}$ ${\displaystyle H}$ ${\displaystyle L(A)}$

${\displaystyle L(A):=H\oplus \sum _{\alpha \in Q}L_{\alpha }}$     With

${\displaystyle L_{\alpha }:=\{y\in L(A)\mid \,[xy]=\alpha (x)y{\text{ für alle }}x\in H\}}$

possible, whereby they are called weights as usual and can be combined linearly from the integral numbers . The foundations of this theory are worked out in the frequently cited textbook by Roger Carter . ${\displaystyle \alpha \in Q\subset H^{*}}$ ${\displaystyle \alpha _{1},\ldots ,\alpha _{n}\in \Pi \subset H^{*}}$

Individual evidence

1. ^ Roger Carter : Lie Algebras of Finite and Affine Type , Cambridge studies in advanced mathematics 96 (2005), ISBN 978-0-521-85138-1 , Chapter 14.1: Realizations of a square matrix
2. ↑ Roger Carter: Lie Algebras of Finite and Affine Type , Cambridge studies in advanced mathematics 96 (2005), ISBN 978-0-521-85138-1 , Chapter 14.3: The Kac-Moody algebra L (A)
3. ^ Roger Carter: Lie Algebras of Finite and Affine Type , Cambridge studies in advanced mathematics 96 (2005), ISBN 978-0-521-85138-1 , Chapter 15.1: A trichotomy for indecomposable GCMs
4. ^ Roger Carter: Lie Algebras of Finite and Affine Type , Cambridge studies in advanced mathematics 96 (2005), ISBN 978-0-521-85138-1 , Chapter 15.1: The classification of affine generalized Cartan matrices