ω-automaton

An ω-automaton ( omega automaton ) is a mathematical model that represents an extension of the finite automaton to the input of infinite words . Finally the called machine , so as the number of its internal states finite. Likewise, the alphabet over which this automaton works is finite.

The Greek letter ω ( omega ) stands for the smallest infinite ordinal number .

The consideration of such machines is motivated by many systems (e.g. operating systems ) which, by definition, should not actually terminate, but rather be operated indefinitely.

description

Based on a special state (starting state) , the ω-automaton reads a countably infinite sequence of symbols (input word) that are elements of a finite set of symbols (input alphabet) .

The ω-automaton proceeds step by step, with the next symbol of the input word being read in each step. The subsequent state is determined by the state transition function depending on the currently read character and the current state. ${\displaystyle \delta }$

The question of whether the input word is accepted depends on the type of ω-automaton. In each case, the set of states is consulted, which are passed through infinitely often.

presentation

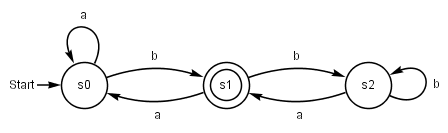
An ω-automaton can be represented both as a state diagram and as a state table:

		a b s0 s0 s1 s1 s0 s2 s2 s1 s2
State diagram		State table

The diagram reads as follows:

• Simple circles represent states .
• The name of the state or the state is in the circle.
• Arrows represent transitions (state transitions). The arrows indicate which characters (or even which words) the automaton reads during the transition.
• The initial state is characterized in that it is the end point of an arrow that does not have a state as a starting point.
• Final states are indicated by double circles (but not all types of ω-automata have final states; the acceptance mechanisms are different).

Types

As with finite automata, a distinction is made between deterministic and nondeterministic automata for ω-automata.

Furthermore, one differentiates between the machines according to the way in which it is decided whether an entered word is accepted or not. In most cases, this acceptance of a word is decided according to the infinitely often assumed states. Examples of ω-automata are the Büchi automaton , the Muller automaton , the Rabin automaton , the Streett automaton and the parity automaton .

Except for the deterministic Büchi automata, all named automata recognize the class of ω-regular expressions (the extension of regular expressions to infinite character strings). The deterministic Büchi automaton recognizes only a subset of these expressions and represents a really weaker automaton class.

Formal definition

An ω-automaton is a 5-tuple:

${\displaystyle M=(\Sigma ,Z,Z_{0},\delta ,Z_{E})}$

The elements are defined as follows:

• ${\displaystyle \Sigma }$is a finite set , the input alphabet, from the elements of which the input words are composed.
• ${\displaystyle Z}$is the finite set of states of the automaton that is too disjoint . ${\displaystyle \Sigma }$
• ${\displaystyle Z_{0}\in Z}$ is the start state.
• ${\displaystyle \delta :\Sigma \times Z\rightarrow Z}$is the transfer function, it is usually total, i.e. H. every element of the set of archetypes has an image. ${\displaystyle \Sigma \times Z}$
• ${\displaystyle Z_{E}}$is a component that is dependent on the type of machine and controls when a word is accepted; in Büchi machines, for example, this is a subset of . ${\displaystyle Z}$

In the case of nondeterministic automata, the (not necessarily total) transfer relation is defined as, where the power set of is. When entering a new character, the automaton can then non-deterministically go into one of several states, which are given by the image (set of states) of the function. ${\displaystyle \Delta :\Sigma \times Z\rightarrow P(Z)}$ ${\displaystyle P(Z)}$ ${\displaystyle Z}$

See also

• Model testing