Braking distance
The braking distance is defined as the distance covered from the moment the braking is initiated until the vehicle or train comes to a standstill or until the braking process reaches its final speed. The time required for this is the braking time (also known as the braking duration ). The braking time in turn contains breakdown, reversal and slip times (unbraked movement) as well as the time for the developing braking friction force (effective braking time).
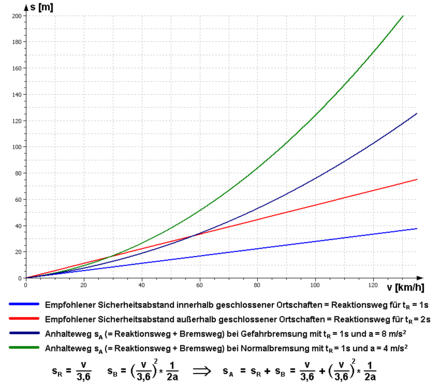
The driving speed and the braking deceleration are decisive for the length of the braking distance . The stopping distance , on the other hand, is longer and also takes into account the reaction path , which is covered without braking and which depends on the reaction time.
In the case of rail vehicles, the graphical representation of the speed over the braking distance covered is called the braking curve and is important for the function of safe stopping by train control systems . The minimum braking deceleration is 5 m / s² according to § 41 Paragraph 4 StVZO for vehicles that drive faster than 25 km / h.
Calculations and physical background
If the initial speed is in m / s and a is the constant braking deceleration in m / s², then the braking distance s B (in m) is:
- (1)
Derivation of this formula:
The following applies to the speed during the braking process:
- (2)
This is that part of the speed that was lost due to braking, i.e. negative acceleration.
The following applies to the distance covered :
- (3)
Explanation:
- is the distance that the object would have traveled if it had not been braked.
- is then the distance that it covers less due to the braking process.
The object finally comes to a standstill when v (t) = 0.
This is now inserted into equation (2):
If you solve this equation for the time t, you get the braking time :
If you insert the braking time into equation (3), you get the formula for the braking distance:
The maximum possible braking deceleration depends on the friction pairing tire / road surface.
Reference values for the maximum braking deceleration of cars in m / s²:
- Dry asphalt surface:> 8
- Sand: 4–5
- Snow-covered road: 1–4
In modern sports cars, the braking deceleration can be greater than the acceleration due to gravity g (~ 9.81 m / s²) , even if the vehicle is only pressed against the road by its weight . With special rubber compounds, static friction coefficients of up to 1.8 can be achieved in automobile racing, and even peak values of 5.0 can be achieved in the short term.
Braking on the incline
When braking on the slippery slope to the Earth's gravity affects. The component of the acceleration due to gravity g parallel to the roadway adds up to the braking deceleration . The resulting delay results:
The angle of inclination of the roadway is positive on an incline.
The maximum braking deceleration parallel to the inclined plane results from:
As above, the following applies to the smallest braking distance :
The deceleration can be zero or negative on slopes ( ) and slippery roads. Then the object is not braked, but faster. Therefore no braking distance can be specified.
Vehicle stopping distance
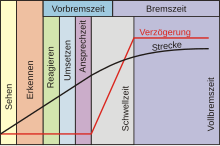
The stopping distance is the distance that a vehicle covers from the point in time at which the obstacle occurs or can be seen to standstill. The detection usually takes about 0.1 s (an instant ). The reaction time is about 0.8 s. If the traffic situation requires increased attention and readiness to react, the reaction and brake response time is a maximum of 0.6 seconds (BGH VRS 6, 13).
The response time (also application time or slip time ) refers to the time from pressing the brake pedal to the first contact of the brake lining with the brake disc or drum. During the response time, the vehicle continues to drive at unbraked speed. The response time can be shortened by reducing the clearance and by using electronic sensors. The sensor and control unit can recognize emergency braking by the rapid change from accelerator to brake pedal and the high speed of brake actuation. The braking is initiated automatically by these brake assistance systems, response and threshold times are shortened by rapid pressure build-up.
The threshold time (i.e. the effective braking time , see figure) is the time that the brakes need to develop their maximum braking effect. With a hydraulic brake system, the time is between 0.1 and 0.2 seconds, with a compressed air brake system between 0.2 and 0.4 seconds. In order to reduce the build-up time in compressed air brake systems, relay valves are installed close to the brake.
For a car driver, the reaction and pre-braking times are assumed to last one second. It is shorter with attentive, experienced drivers. Drugs, alcohol and medication significantly extend it. The response time largely determines the length of the necessary safety distance .
Wheel rail
In the case of trains, the braking delay is approx. 1 m / s², which results from the lower friction between the metal surfaces of the wheel and rail . With the same initial speed, the braking distance of a train is about ten times longer than that of a car. The braking distance of a 90 km / h stopping train is over 313 meters. In the Netherlands, express trains travel at speeds of 110–125 km / h and have a minimum braking distance of more than half a kilometer. High-speed trains travel at speeds of 220–320 km / h, which means that their minimum braking distance is two to more than five kilometers.
Ships
Ships are mainly braked by a targeted increase in hydrodynamic resistance. However, other means, such as casting anchors and adjusting sails appropriately to reduce speed, are also possible.
The main method used for active braking is to reverse the thrust of the drive. For this purpose, in the case of propellers and paddle wheels, the direction of rotation is reversed, in the case of water jet propulsion the jet is deflected. Since ships are relatively heavy and the medium water with its relatively low viscosity offers only a low flow resistance, large ships usually brake more slowly than cars and trains. Ships with a high ratio of engine power per unit of mass such as light cruisers and tugs therefore have a comparatively high braking deceleration.
The smaller a boat is, the faster it is slowed down by the drag: a rudder eight runs out several dozen meters without a belt. A single kayak or small rubber dinghy can only run a few meters without paddling. The International Maritime Organization stipulates that ships must come to a stop within 15 (in exceptional cases 20) ship lengths in the event of an emergency stop maneuver from full speed. Such a maneuver loads the main engine , its foundations and the shaft so much that this is only practiced in exceptional cases, except for the technical acceptance. With a maximum ship length of 450 m, the regulations would result in a maximum distance of 9 km (4.9 nm) for this vehicle to come to a standstill in an emergency.
See also
- ABS (anti-lock braking system)
- Braking time
- Brake (railway)
- Sand spreader
Web links
Individual evidence
- ↑ Braking delay and extrapolation. WABCO Basic Course 23 (PDF), p. 2 ( page can no longer be accessed , search in web archives ) Info: The link was automatically marked as defective. Please check the link according to the instructions and then remove this notice. , last accessed April 26, 2016.
- ^ Bosch: Kraftfahrtechnisches Taschenbuch , 26th edition 2007, ISBN 978-3-8348-0138-8 , p. 435.
- ↑ Michael Trzesniowski: racing car technology . 2nd Edition. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-0857-8 , p. 204.