Daisyworld
Daisyworld is a computer simulation of a hypothetical planet orbiting a sun-like star , whose radiation output and thus temperature, like the sun, increases slowly over the course of billions of years, although the global average temperature of the planet remains approximately constant over a long period of time due to self-organizing biological feedback processes . James Lovelock and Andrew Watson published this model in 1983 in order to underpin the plausibility of the Gaia hypothesis , which postulates a self-regulation of various environmental parameters of a living planet by life itself.
The Daisyworld model
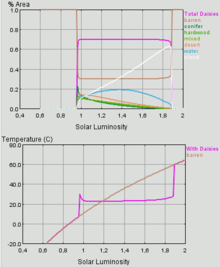
In the computer simulation Daisyworld there are only two types of living beings on a simulated Earth-like planet : black daisys ( daisies ) and white daisys. White daisys have white flowers that reflect light and black daisys have black flowers that absorb light. Both species have the same growth curve (their rate of reproduction has the same dependence on temperature), but because of their black flowers, black daisys are warmer than white daisys and bare soil. A planet with a preponderance of white daisys is cooler than one with more black ones.
At the beginning of the simulation, the planet Daisyworld is so cold that only a few black Daisys and almost no white Daisys can survive. Every time the temperature drops, the black flowers begin to dominate. These absorb the heat from the sun, which in turn causes the temperature of the planet to rise. This in turn leads to better growth of the black daisys and this to a further increase in temperature. With the warming of the planet, white daisys can now reproduce better, which due to their lower temperature have a better reproduction rate than the black and hotter daisys that are now above their optimum. The planet reaches a temperature equilibrium. Every warming leads to a larger number of white daisys, every cooling to more black daisys. Such a system is remarkably stable in relation to the changing radiant power of the sun. The entire planet regulates itself . At some point, however, the external radiant power exceeds the regulatory powers of the competing daisys and the planet is overwhelmed by heat.
If the simulation is run without the Daisys, the temperature profile increases synchronously with the radiation output of the sun. With Daisys, there is increased heating at the beginning of the simulation and increased cooling at the end, resulting in an almost constant equilibrium temperature for most of the simulation. In this way, the Daisys change the climate in such a way that the conditions become more livable for them. However, Daisy World model for certain shows solar constant and hysteresis , so that the planet two different stable states for this solar constant has: Typically, each of the abiotic and the other almost completely populated.
Later extensions of the Daisyworld model included so-called rabbits, foxes and other species that have absorption rates between the black and white daisys. One of the more surprising results of these simulations was that the self-regulating forces of the entire planet increased with the number of species. This observation supported the view that biodiversity is valuable and sparked the modern biodiversity debate.
Daisyworld also drew criticism. The simulation shows little resemblance to Earth ; the system requires an ad hoc death rate (γ) to maintain equilibrium, and the model blurs the differences between phenomena at the species and individual levels. However, Daisyworld undeniably shows that biologically regulated equilibrium does not need a teleological explanation.
Trivia
A version of the Daisyworld simulation was built into the SimEarth computer game by Maxis .
literature
- Andrew J. Watson and James E. Lovelock: Biological homeostasis of the global environment. The parable of Daisyworld . In: Tellus , Vol. 35 / B (1983), pp. 286-289 (the original Watson and Lovelock publication introducing the Daisyworld model); online (PDF; 566 kB).
Web links
- Modeling of Daisyworld including the equations used in it
- James Lovelock's Daisyworld material on the subject of "Complex Systems in Physics Lessons" by Rolf Carstensen, Institute for Science Education, University of Kiel