Delaunay triangulation

The Delaunay triangulation (more rarely also Delaunay triangulation ) is a common method to create a triangular network from a set of points . It is named after the Russian mathematician Boris Nikolajewitsch Delone (1890–1980, French form of the surname: Delaunay ), who dealt with it in a 1934 publication.

principle

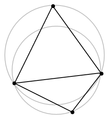
With the Delaunay triangulation process, points are linked to form triangles in such a way that no other points are contained within the circle on which the three triangle points lie ( circumference of the triangle). The method is used, for example, to optimize calculation networks for the finite element method . ${\ displaystyle \ mathbb {R} ^ {2}}$

In a Delaunay triangulation, all triangles of the triangular network fulfill the so-called circumcircle condition : The circumcircle of a triangle of the network must not contain any further points from the specified point set. As a result, mathematically speaking, “the smallest interior angle is maximized over all triangles”. Too good German, it is guaranteed that the smallest angle in the triangles will be as large as it can be in this triangular network. However, no statement is made about the other angles.

The Delaunay triangulation is not unambiguous if there are more than three points on a circumference, ie the user can freely choose which three points he connects to a triangle.

In two-dimensional meshes, Delaunay generally leads to triangles with relatively large interior angles . This property is very desirable in computer graphics because it minimizes rounding errors.

In three-dimensional space, instead of the circumcircle condition , the analogous circumference condition is used, which then creates a tetrahedron from four points . However, Delaunay triangulation in 3D or higher spaces can lead to the formation of artifacts called slivers. These artifacts have negative properties for computer graphics, finite element methods, and many other applications. Therefore Delaunay is not an independent means of generating computer graphics, but must be accompanied by error handling.

Relation to Voronoi diagrams

The Delaunay triangulation is the dual graph of the Voronoi diagram of the point set: The corners of the Voronoy cells are the circumcenters of the triangles of the Delaunay triangulation. The Voronoi cells are obtained by drawing the perpendiculars from all sides of the triangle up to the common point of intersection with the other two perpendiculars of the same triangle. In the case of obtuse triangles, this point may well lie outside the triangle surface. For right triangles, it is the point that bisects the hypotenuse .

Delaunay triangulation of a set of points in the plane.
Voronoi diagram of the same set of points.
Voronoi diagram (orange) and Delaunay triangulation (black)

Algorithms

There are several approaches to performing Delaunay triangulation. The best runtime achieved is with a storage space requirement of . ${\ displaystyle {\ mathcal {O}} (n \ cdot \ log (n))}$ ${\ displaystyle {\ mathcal {O}} (n)}$

Flip

The flip algorithm is a special version for two-dimensional triangular networks. It is based on a local evaluation of the perimeter condition.

First, any triangular mesh is generated using a simple algorithm. This does not have to fulfill the circumcircle condition by any means, it simply must not contain any overlapping edges.

For each triangle it is checked whether the perimeter of this triangle includes another point that is part of an adjacent triangle. In this case, a flip of the common edge is performed. That is, the common edge is replaced by a new edge that connects the two points that were not connected before. After the flip, the perimeter condition is met locally. However, this may have disturbed the circumcircle condition in the neighboring triangles again. In the worst case, all other triangles would have to be checked again after a flip, which is why the computing effort of the flip algorithm is. ${\ displaystyle \ Theta (n ^ {2})}$

These two triangles do not meet the circumcircle condition.
After the flip, the perimeter condition (local) is fulfilled.

Incremental construction

In the incremental method, the points are added one at a time. In contrast to the other methods, not only can the Delaunay triangulation of a fixed set of points be generated, but it can also be expanded later with points that were not yet known at the beginning and are only determined by a process. The core of this method is an algorithm that assumes an existing Delaunay triangulation and adds a point within it. As an initialization, it is sufficient to specify a triangle that includes the area of all points to be expected. The algorithm can be divided into three steps:

In the triangulation, the triangle that contains the new point is searched for. A naive way of simply testing every triangle has the effort . ${\ displaystyle \ Theta (n)}$
The new point is connected to the three corners of the triangle found, so that three new triangles are created. This triangulation may no longer meet the Delaunay condition.
Each of the three new triangles is then tested for the circumference condition and, if necessary, corrected as in the flip algorithm. After each correction, there are further triangles that may no longer meet the perimeter condition. This testing and correction continues through the triangulation until all triangles meet the perimeter condition. Since in the worst case all triangles have to be corrected, the worst case is effort . But this case will rarely occur. If the points are inserted in a random order, usually only a limited number of corrections have to be carried out, so that an average effort is to be expected. ${\ displaystyle \ Theta (n)}$ ${\ displaystyle {\ mathcal {O}} (1)}$

Carrying out the search method with for all n points takes the effort . The corrections for n points (in random order) only . The total effort is therefore determined by the search. A simple way of improving the search is to run the triangulation starting from any triangle in the direction of the point you are looking for. The hassle of this method is . A more complicated search can be implemented by storing the history of all triangles created in a tree. Although this tree structure requires additional storage space, it improves the search and thus the entire incremental algorithm . ${\ displaystyle \ Theta (n)}$ ${\ displaystyle \ Theta (n ^ {2})}$ ${\ displaystyle {\ mathcal {O}} (n)}$ ${\ displaystyle {\ mathcal {O}} ({\ sqrt {n}})}$ ${\ displaystyle {\ mathcal {O}} (n \ log {n})}$

Divide and conquer

The divide-and- conquer approach combines two Delaunay triangulations while maintaining the Delaunay condition. The computing effort is included . ${\ displaystyle {\ mathcal {O}} (n \, \ log \, n)}$

Sweep

The sweep algorithm always adds a triangle in compliance with the Delaunay condition. In contrast to the incremental construction, an adjacent triangle is always added here, whereas any triangle can be added in the incremental construction. The computing effort is included . ${\ displaystyle {\ mathcal {O}} (n \, \ log \, n)}$

Voronoi

In the Voronoi approach, the Voronoi graph is first formed for all points. Due to the duality of the triangular network, you have already determined all the necessary circumferential centers and now only have to draw the corresponding circles.

Calculation over the convex hull in 3D

Each 2D point is expanded by a z coordinate . The convex hull - a surface faceted with triangles - is created around these 3D points . The orientation of the triangle normals is determined to the outside. If all triangles oriented downwards (i.e. those with a negative z-coordinate of their normal vector ) are projected back into the original xy-plane , the 2D Delaunay triangular network is obtained there. The time required is in . ${\ displaystyle z = x ^ {2} + y ^ {2}}$ ${\ displaystyle {\ mathcal {O}} (n \, \ log \, n)}$

application

The Delaunay triangulation allows, for example, a simple proof for Thue's theorem , which says that the hexagonal circle packing is the closest of all possible circle packing .

literature

R. Klein: Algorithmic Geometry. Springer, 2005, ISBN 3-540-20956-5 .
F. Aurenhammer, R. Klein: Voronoi Diagrams. (PDF; 856 kB).
A. Okabe et al: Spatial Tessellations: Concepts and Applications of Voronoi Diagrams. Wiley, 2000, ISBN 0-471-98635-6 .

credentials

^ Boris N. Delaunay: Sur la sphère vide. In: Bulletin of Academy of Sciences of the USSR. 7, No. 6, 1934, pp. 793-800.
^ Pavel Maur: Delaunay Triangulation in 3d state of the art and doctoral thesis. (PDF) In: Technical Report. University of West Bohemia, February 1, 2002, pp. 3–4 , accessed July 4, 2020 .
↑ ^a ^b Jianwei Guo, Dong-Ming Yan, Li Chen, Xiaopeng Zhang, Oliver Deussen: Tetrahedral meshing via maximal Poisson disk sampling . In: Computer Aided Geometric Design . tape 43 , March 2016, 4th Tetrahedral Meshing, pp. 186–199 , doi : 10.1016 / j.cagd.2016.02.004 ( elsevier.com [accessed on July 4, 2020]): "In 3D, even well-spaced vertices could create degenerate 3D elements (eg, slivers)."
↑ F. Aurenhammer, R. Klein: Voronoi Diagrams. (PDF; 856 kB).
^ ^A ^b P. Su, RLS Drysdale: A Comparison of Sequential Delaunay Triangulation Algorithms. In: Computational Geometry: Theory and Applications. v7 n5, 1997, pp. 361-385.
↑ Rolf Klein: Algorithmic Geometry . Springer, 2005, ISBN 3-540-20956-5 , pp. 304ff.
↑ Hai-Chau Chang, Lih-Chung Wang: A Simple Proof of Thue's Theorem on Circle Packing. 2010, arxiv : 1009.4322 .