Deontic logic

Deontic logic is the area of logic that examines the logical relationships of terms that relate to the ought . Terms related to the ought are command ( duty ), prohibition , permission and others.

Etymologically, the expression comes from the ancient Greek δέον déon (Gen. δέοντος déontos ). "to déon" is translated in different ways: among other things with the necessary , the appropriate , the "necessary", "the necessary", the "duty".

The term ontic logic is occasionally formed as an opposite term . "Ontic logic" is then the logic of sentences (only) about being.

Sentences about being have (in two-valued) logic the truth values true or not true ( false ). Sentences about the ought are not true or false, but valid or not valid ( invalid ).

Note the difference between is standard and a standard set of "norms enjoin, prohibit or allow certain behavior, authority records say other hand, that a certain behavior commanded or forbidden is allowed.". Depending on the context, the same sentence can express a norm or an authority sentence. The sentence "Murder is forbidden" can mean the prohibition of murder (norm) or the assertion that murder is forbidden (norm sentence). An authority sentence as an assertion about a norm can be true or false.

Deontic logic is a formal , philosophical , non-classical logic. It is viewed as an application of modal logic , as "modal logic in the broader sense" or (only) as logic based on modal logic.

Like ontic logic, modern deontic logic is formalized and, if possible, operated in a calculated manner. There are different views on the basic deontic ( deontological ) terms to be used.

Basic deontic terms

Basic deontic terms are required and prohibited .

A restriction to this would mean that everything that is not required would be prohibited.

Aristotle is believed to have assumed that a specific act was either required or prohibited.

The (general) modal logic knows three basic concepts and their negations: necessary / unnecessary , impossible / possible contingent / not contingent . In analogy to this, three basic deontic concepts and their negation are assumed: required / not required , forbidden / not forbidden and indifferent / not indifferent .

Instead of indifferent one also speaks of "exempted" or "indifferent".

It is emphasized that "allowed" can have (at least) two different meanings: on the one hand as "not forbidden" (from a certain prohibition): relatively allowed ( not forbidden ), which does not exclude that something is required . Allowed can also be meant in an absolute sense, i.e. H. something is neither forbidden nor required: indifferent .

syntax

The formalized deontic logic uses linguistic signs to abbreviate the basic deontic terms called deontic operators . These can vary from language to language and from author to author within a language. The following are common:

• It is imperative: O (from obligatory );
• It is forbidden: V , also F (from forbidden );
• It is allowed: E , also P (from permitted );
• It is up to: I .

This enables, for example, the following atomic deontic sentences:

• For "It is necessary to do the action p ", one can write "O (p)" in a formalized way.
• For "It is imperative that the individual a does the action p , one can write" O (p (a)) ".

Illustrations

The relationships between the basic deontological concepts are presented in different ways. On the one hand as logical squares or as deontological hexagonal

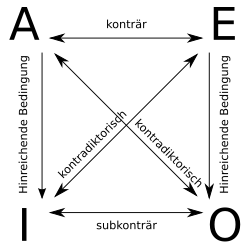
logical square

The logical square

If the relationships are represented as a deontic logical square ("norm square"), it should be noted that a distinction must be made between a command and a permission square.

In the bid square, "A" stands for commandment ( O ), "E" for prohibition ( F ), "I" for permission and O for "It is not forbidden".

In the permission square, "A" stands for "¬ P (¬ p)", "E" for "¬ P (p)", "I" for "P (p)" and "O" for "P (¬ p)" .

(Translated: "Is not allowed that not p" ("A") is contradictory to "It is allowed that p" ("O"). "A" contains "subaltern" "I", ie "It is allowed that p "." I "is contradictory to" E ", ie" It is not allowed that p "." A "and" E "are contrary, ie are mutually exclusive. It cannot be at the same time that p is not is allowed ("E") and that it is not allowed that not p is ("A").)

deontological hexagon

Analogous to modal logic, a deontological hexagon can also be used as a basis for the three basic concepts and their negations to illustrate the relationships between the basic concepts

Operator equivalences

As in modal logic, there are operator equivalences :

• Example: F (p) ↔ O (¬ p)

"Exactly when it is forbidden to perform the action described by p, it is imperative not to perform the action described by p = the prohibition corresponds to the commandment to omit."

• Example: O (p) ↔ F (¬ p)

"Exactly when it is necessary to perform the action described by p, it is forbidden not to perform the action described by p = the commandment corresponds to the prohibition of omission."

history

Early Deontic Logic

Philosophers of the Indian Mimamsa school and the ancient Greeks noticed the formal logical relations of the deontic concepts. Late Middle Ages philosophers compared deontic concepts to alethic ones . In Elementa juris naturalis , Leibniz noted that the logical relations between licitum (allowed), illicitum (forbidden), debitum (required) and indifferent (irrelevant) are equivalent to those between possibile (possible), impossibile (impossible), necessarium (necessary) and contingens (contingent).

Mally's first Deontic Logic

Ernst Mally , a student of Alexius Meinong , was the first to propose a formal system of deontic logic in the basic laws of ought , based on the syntax of Whitehead and Russell's propositional calculus . Mally's deontic vocabulary consisted of the logical constants U and ∩, the single-valued connectivity! and the two-valued connectives f and ∞.

* Mally read! A as "A shall be the case".
* He read A f B as "A needs B".
* He read A ∞ B as "A and B need each other."
* He read U as "unconditional commitment".
* He read ∩ as "unconditional prohibition".

Mally defined f, ∞ and ∩ as follows:

Def. F. A f B = A →! B
Def. ∞. A ∞ B = (A f B) & (B f ​​A)
Def. ∩. ∩ = ¬U

Mally suggested five informal principles:

(i) If AB needs and if it follows from BC, then A needs C.
(ii) If AB needs and if AC needs, then AB and C.
(iii) A needs B if and only if it is mandatory that B follows from A.
(iv) The unconditional commitment is mandatory.
(v) The unconditional obligation does not need its own negation.

He formalized these principles as his axioms:

I. ((A f B) & (B → C)) → (A f C)
II. ((A f B) & (A f C)) → (A f (B & C))
III. (A f B) ↔! (A → B)
IV. ∃U! U
V. ¬ (U f ∩)

From these axioms, Mally deduced 35 theorems, many of which he found strange. The axioms III. and IV. mix factual sentences and norms and thus violate Hume's law . Karl Menger showed that! A ↔ A is a theorem so that the introduction of the sign! is irrelevant because Mally is supposed to have A when A is the case, which discredited Mally's system. Mally introduced the term "deontisch" in German.

From Wright's First Meaningful Deontic Logic

The first meaningful system of deontic logic was suggested by GH von Wright . Von Wright introduced the term deontic in English. Since then, many philosophers and computer scientists have developed many systems of deontic logic. Nevertheless, deontic logic remained one of the most controversial branches of logic.

In 1951, GH von Wright based his deontic logic not on the syntax of propositional calculus like Mally, but on Leibniz's alethic modal logic , which Mally had ignored. But in 1964 he returned to the syntax of propositional calculus in A New System of Deontic Logic , which he explained in more detail in Deontic Logic: A Personal View and A New System of Deontic Logic .

Classic deontic logic

In von Wright's first system, obligation and permissibility were understood as characteristics of action. But soon afterwards it was found that a deontic logic of statements could be given simple and elegant Kripke semantics , and Wright followed suit. The so specified deontic logic was the "Classical deontic logic", often referred to as SDL , KD or simply D . It is axiomatized by the following addition to the classical propositional logic :

${\displaystyle O(A\rightarrow B)\rightarrow (OA\rightarrow OB)}$

${\displaystyle OA\to \lnot O\lnot A}$

The axioms state:

• If it should be that AB implies, then B should be if A should be.
• If A is supposed to be, then it is not mandatory that A is not.

FA means that A is forbidden and is formally defined as or . ${\displaystyle O\lnot A}$ ${\displaystyle \lnot PA}$

There are two important extensions of SDL : The first is the addition of an alethic modal operator to express Kant's thesis that should be able to imply: ${\displaystyle \Box }$

${\displaystyle OA\to \Diamond A.}$

whereby . Most of the time it is considered to be at least a KT operator, usually even an S5 operator. ${\displaystyle \Diamond \equiv \lnot \Box \lnot }$ ${\displaystyle \Box }$

The second important addition consists of adding an operator to the conditional obligation O (A / B): "It is mandatory that A if B". The supplement is motivated by the following case: It applies that the hungry should be cared for. If the hungry are cared for, it follows that there are hungry people. It follows from the basic principles of the SDL that there should be hungry people. The argument is valid in every normal modal logic because of the basic axiom K of the SDL and the principle:

${\displaystyle \vdash A\to B\Rightarrow \ \vdash OA\to OB.}$

If one introduces an intensional conditional operator, one can say: The hungry should be cared for, but only if there are actually hungry, formally written O (A / B). From this one can no longer deduce that there should be hungry people.

Dyadic deontic logic

An important problem of deontic logic is the correct representation of conditional obligations, e.g. B. If you smoke (s), use an ashtray (a)! It is unclear whether any of the following representations are adequate:

${\displaystyle O(\mathrm {smoke} \rightarrow \mathrm {ashtray} )}$

${\displaystyle \mathrm {smoke} \rightarrow O(\mathrm {ashtray} )}$

In the first representation, it is a void truth that if you break a prohibition you have to take some further action, regardless of whether it is mandatory, permitted or prohibited.

In the second representation, the killer paradox arises: From (1) If you murder, do it gently! , (2) You murder. and (3) To murder gently, you must murder. the result is: you should murder!

Some deontic logicians have responded by developing dyadic deontic logics that include binary deontic operators:

${\displaystyle O(A\mid B)}$means it is mandatory that A, if B

${\displaystyle P(A\mid B)}$ie it is permissible that A if B .

(The notation follows that for conditional probability .) Dyadic deontic logic does not have the problem of deontic logic with single-valued operators, but has other problems.

Other variations

Many other variants of Deontic Logic have been developed, e.g. B. non-monotonous deontic logics, paraconsistent deontic logics and dynamic deontic logic. After presenting individual systems, Edgar Morscher provides a review of the history of norm logic since "Ernst Mally's false start" in the 15th chapter of his book "Normlogik" (2012).

Jørgensen's dilemma

Deontic logic has a problem - Jørgensen's dilemma. Norms are not truthful, but truth values are used in logic . There are two possible answers:

• Deontic logic deals with logical statements about norms, not norms.
• Alternative theories of truth, e.g. B. Truth as general validity or as success as in speech act theory.
• Extension of the concept of inference so that truth-preserving inference is viewed as a special case of logical inference at all. (But even then, no propositional sentences can be inferred from normative sentences; and no normative sentences from declarative sentences. An argument for an ought must then renounce the truth claim or its validity assert without claiming truth. That does not correspond to the normal use of arguments. If one abandons the truth functionality of logical inference, then logic becomes the mere art of formalization.)

See also

• Modal logic

Individual evidence

1. ↑ Jan C. Joerden : Deontic logic. , in: Eric Hilgendorf , Jan C. Joerden (ed.): Handbuch Rechtssphilosophie. Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1 , p. 242
2. ↑ Jan C. Joerden : Deontic logic. , in: Eric Hilgendorf , Jan C. Joerden (ed.): Handbuch Rechtssphilosophie. Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1 , p. 242
3. ↑ Hans-Joachim Koch , Helmut Rüßmann : Legal Justification: An Introduction to Basic Problems of Law. Munich: Beck, 1982 (series of legal training; issue 22), ISBN 3-406-03452-7 , p. 45
4. ↑ Cf. Hans-Joachim Koch , Helmut Rüßmann : Juristische Justification Doctrine: An Introduction to Basic Problems in Law. Munich: Beck, 1982 (series of legal training; issue 22), ISBN 3-406-03452-7 , p. 45
5. ↑ Jan C. Joerden : Deontic logic. , in: Eric Hilgendorf , Jan C. Joerden (ed.): Handbuch Rechtssphilosophie. Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1 , p. 242
6. ^ So Jan C. Joerden : Deontic logic. , in: Eric Hilgendorf , Jan C. Joerden (ed.): Handbuch Rechtssphilosophie. Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1 , p. 242 (243)
7. ^ So Jan C. Joerden : Deontic logic. , in: Eric Hilgendorf , Jan C. Joerden (ed.): Handbuch Rechtssphilosophie. Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1 , p. 242 (243)
8. ↑ Cf. Hans-Joachim Koch , Helmut Rüßmann : Juristische Justification Doctrine: An Introduction to Basic Problems in Law. Munich: Beck, 1982 (series of legal training; issue 22), ISBN 3-406-03452-7 , p. 45 ( using instead of p F )
9. ^ Röhl, Klaus F .; Hans Christian Röhl: General legal theory. 3. Edition. C. Heymanns, Cologne a. a. 2008, § 22 II, p. 192
10. ↑ See Strobach, Introduction to Logic (2005), p. 117
11. ↑ After Herberger, Maximilian; Dieter Simon: Theory of Science for Lawyers. Metzner, Frankfurt a. M. 1980, p. 185
12. ↑ See Jan C. Joerden : Deontic Logic. , in: Eric Hilgendorf , Jan C. Joerden (ed.): Handbuch Rechtssphilosophie. Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1 , p. 242 (243)
13. ↑ Herberger, Maximilian; Dieter Simon: Theory of Science for Lawyers. Metzner, Frankfurt a. M. 1980, p. 184
14. ↑ Herberger, Maximilian; Dieter Simon: Theory of Science for Lawyers. Metzner, Frankfurt a. M. 1980, p. 184
15. ↑ Huisjes, CH, 1981, "Norms and logic," Thesis, University of Groningen
16. ↑ Knuuttila, Simo, 1981, “The Emergence of Deontic Logic in the Fourteenth Century,” in New Studies in Deontic Logic, Ed. Hilpinen, Risto, pp. 225-248, University of Turku, Turku, Finland: D. Reidel Publishing Company.
17. ↑ Menger, Karl, 1939, "A logic of the doubtful: On optative and imperative logic," in Reports of a Mathematical Colloquium, 2nd series, 2nd issue, pp. 53-64, Notre Dame, Indiana: Indiana University Press.
18. ↑ Mally's Deontic Logic by Gert Lokhorst in the Stanford Encyclopedia of Philosophy
19. ↑ Mally, Deontik , 1926
20. ^ GH von Wright, Deontic Logic in: Mind , 1951
21. ↑ Albert JJ Anglberger, A Possible Worlds Semantics for GH von Wright's first calculus of deontic logic in: Conceptus-Zeitschrift für Philosophie , No. 89-90, 2004
22. ↑ Albert JJ Anglberger, Non-Cognitivism and Norm Logic : Considerations on a multi-valued Possible World Semantics , in: Kreuzbauer, G./Gratzl, N./Hiebl, E. (Eds.): Persuasion and Science: Current Issues of Rhetoric and Argumentation Theory 2006 , Vienna, LIT-Verlag, 2007
23. ↑ From Wright 1956, cited in Aqvist 1994

literature

• Jan C. Joerden : Deontic Logic , in: Eric Hilgendorf , Jan C. Joerden (ed.): Handbuch Rechtssphilosophie Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1 , pp. 242–245
• Lennart Åqvist , 1994, "Deontic Logic" in D. Gabbay and F. Guenthner, ed., Handbook of Philosophical Logic: Volume II Extensions of Classical Logic . Kluwer.
• Hilpinen, Risto, 2001, "Deontic Logic," in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic . Blackwell.
• GH von Wright , 1951. "Deontic logic," Mind 60 : 1-15.
• Franz von Kutschera : Introduction to the logic of norms, values ​​and decisions. Freiburg i. Br./ Munich, Alber, 1973.
• Hans Lenk (ed.): Norm logic. Basic problems of deontic logic. Pullach near Munich, Verlag Documentation, 1974.

Web links

• McNamara, Deontic Logic , Stanford Encyclopedia of Philosophy , 2006.
• KED (PDF file; 91 kB) - Hyperlink invalid!