Bell-shaped function

The density function of the normal distribution is an archetypal example of a bell-shaped function

A bell-shaped function is a function from to whose graph has a characteristic "bell shape". Such functions are often chosen regularly (e.g. continuous or even smooth ) and they converge for towards 0. In addition, they have a single global maximum, often at . The antiderivatives of bell-shaped functions are therefore mostly sigmoid functions . Bell-shaped functions are often mirror-symmetric to the axis on which the maximum is assumed. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle x\to \pm \infty }$ ${\displaystyle x=0}$

Many commonly used probability density functions are bell-shaped.

Some bell-shaped functions, such as the density functions of the normal distribution or the Cauchy distribution , can be used to construct Dirac sequences . These are function sequences with decreasing variance, which ( in the sense of distributions ) converge to a delta distribution .

Examples

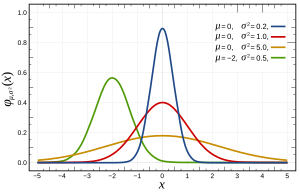
• The density functions of the normal distribution. This often occurs in practical applications (see central limit theorem ).

${\displaystyle f(x)=ae^{-(x-b)^{2}/(2c^{2})}}$

• The generalized membership function of fuzzy logic

${\displaystyle f(x)={\frac {1}{1+\left|{\frac {x-c}{a}}\right|^{2b}}}}$

• The hyperbolic secant

${\displaystyle f(x)=\operatorname {sech} (x)={\frac {2}{e^{x}+e^{-x}}}}$

• The Versiera of Agnesi , density function of the Cauchy distribution

${\displaystyle f(x)={\frac {8a^{3}}{x^{2}+4a^{2}}}}$

• An often used test function

${\displaystyle \varphi _{b}(x)={\begin{cases}\exp {\frac {b^{2}}{x^{2}-b^{2}}}&|x|<b,\\0&|x|\geq b.\end{cases}}}$

• Many window functions , such as B. the Kaiser window

• The derivation of the logistic function .

${\displaystyle f(x)={\frac {e^{x}}{\left(1+e^{x}\right)^{2}}}}$

• Some algebraic functions such as

${\displaystyle f(x)={\frac {1}{(1+x^{2})^{3/2}}}}$

gallery

• 

  ${\displaystyle f(x)=\operatorname {sech} (x)}$ (blue)

• 

  Versiera of the Agnesi

• 

  A test function with carrier ${\displaystyle [-1,1]}$

• 

  Kaiser window

Individual evidence

1. ^ Fuzzy Logic Membership Function . Retrieved December 29, 2018.
2. ↑ Generalized bell-shaped membership function . Retrieved December 29, 2018.