Homotopy method

Homotopy methods (also known as homotopy method , continuation or embedding method) are calculation methods in numerical mathematics for the determination of solutions to nonlinear systems of equations . The aim is to enlarge the convergence range of a method for solving nonlinear systems of equations (such as Newton's method).

Preview

A solution to a nonlinear system of equations is a point that usually satisfies nonlinear conditions that are combined into a vector-valued nonlinear function (figure) . In many applications the function contains problem parameters, for example , which can have different values. A well-known example is the real pendulum whose period of oscillation depends non-linearly on the reduced pendulum length. In this case the system of equations reads more correctly , and the solution also depends on the parameter and therefore forms a solution curve with it ${\displaystyle F(x)=0}$ ${\displaystyle x\in \mathbb {R} ^{n}}$ ${\displaystyle n}$ ${\displaystyle F_{1}(x)=F_{2}(x)=\cdots =F_{n}(x)=0}$ ${\displaystyle F:\,\mathbb {R} ^{n}\to \mathbb {R} ^{n}}$ ${\displaystyle F}$ ${\displaystyle t\in \mathbb {R} }$ ${\displaystyle F(x,t)=0}$ ${\displaystyle x}$ ${\displaystyle t}$ ${\displaystyle x\colon [0,1]\to \mathbb {R} ^{n}}$

${\displaystyle F{\bigl (}x(t),t{\bigr )}=0}$ for all ${\displaystyle t\in [0,1]}$

As a possible range of the parameter thereby is without loss of generality , the interval chosen. The existence of a smooth curve follows from the theorem on implicit functions under suitable conditions . Homotopy methods are numerical methods that follow such implicitly defined curves. ${\displaystyle t}$ ${\displaystyle [0,1]}$

Homotopy for nonlinear systems of equations

A fundamental difficulty when using the Newton method is the determination of a starting approximation that has to be close enough to the solution to achieve convergence. This problem can be avoided by embedding it in a homotopy and following the solution curve. Let it now be the nonlinear system of equations to be solved with solution . Then you can get through ${\displaystyle {\hat {x}}}$ ${\displaystyle G(x)=0,\ x\in \mathbb {R} ^{n}}$ ${\displaystyle {\hat {x}}}$

${\displaystyle F(x,t)=0,\quad F(x,t):=G(x)-(1-t)G(y),\quad t\in [0,1],}$

Define an auxiliary problem with a fixed one, the solution of which is known at the point : obviously results . On the other hand with is sought solution just entered in the place : so . With the method described in the following section, the curve can now be followed from the known solution in to the one sought in . ${\displaystyle y\in \mathbb {R} ^{n}}$ ${\displaystyle t=0}$ ${\displaystyle 0{\stackrel {!}{=}}F(x,0)=G(x)-G(y)}$ ${\displaystyle x(0)=y}$ ${\displaystyle G}$ ${\displaystyle t=1}$ ${\displaystyle 0{\stackrel {!}{=}}F(x,1)=G(x)}$ ${\displaystyle {\hat {x}}=x(1)}$ ${\displaystyle x(t)}$ ${\displaystyle t=0}$ ${\displaystyle t=1}$

Numerical curve tracking

The Newton method already mentioned converges very quickly (quadratically), but only locally if the starting approximation is sufficiently precise. This is used when following the curve that the parameter is increased in small steps, for example from to . Then the old solution for a small step size is a good starting approximation for the problem : ${\displaystyle t}$ ${\displaystyle 0\leq t_{m-1}}$ ${\displaystyle t_{m}=t_{m-1}+h_{m}\,}$ ${\displaystyle x(t_{m-1})}$ ${\displaystyle h_{m}}$ ${\displaystyle F(x(t_{m}),t_{m})=0}$

Trivial predictor

${\displaystyle \,\!x_{0}(t_{m}):=x(t_{m-1})}$,

Proofreading iteration

${\displaystyle \left.{\begin{array}{rl}D_{x}F(x_{k}(t_{m}),t_{m})v_{k}=&-F(x_{k}(t_{m}),t_{m}),\\[0.3em]x_{k+1}(t_{m})=&x_{k}(t_{m})+v_{k},\end{array}}\right\}k=0,1,\ldots .}$

This is a shorthand notation for the quadratic Jacobi matrix of the partial derivatives according to the variables . ${\displaystyle \,\!D_{x}F}$ ${\displaystyle x_{1},\ldots ,x_{n}}$

It forms the matrix of the linear system of equations that has to be solved for the corrections in every Newton step . The first diagram shows a sketch of this procedure. ${\displaystyle s_{k}}$

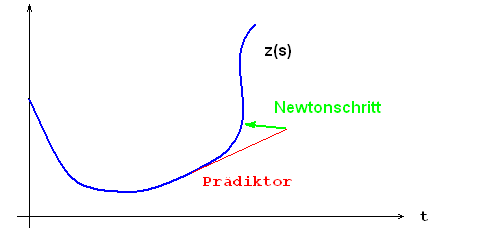
The second diagram shows that you get a better starting approximation if you go from the point in the direction of the curve tangent. The tangent can be determined using the chain rule . Because the function vanishes identically, so does its derivation, ${\displaystyle x(t_{m-1})}$ ${\displaystyle F(x(t),t)}$

${\displaystyle 0\equiv {\frac {d}{dt}}F(x(t),t)=D_{x}F(x(t),t)x'(t)+D_{t}F(x(t),t).}$

The tangent direction at the point can therefore be determined from a linear system of equations. This procedure is as follows: ${\displaystyle t_{m-1}}$ ${\displaystyle z_{m-1}:=x'(t_{m-1})}$

Tangential predictor

${\displaystyle \left.{\begin{array}{rl}D_{x}F{\big (}x(t_{m-1}),t_{m-1}{\big )}z_{m-1}=&-D_{t}F{\big (}x(t_{m-1}),t_{m-1}{\big )},\\[0.3em]x_{0}(t_{m})=&x(t_{m-1})+h_{m}z_{m-1},\end{array}}\right\}}$

Proofreading iteration

${\displaystyle \left.{\begin{array}{rl}D_{x}F(x_{k}(t_{m}),t_{m})v_{k}=&-F(x_{k}(t_{m}),t_{m}),\\x_{k+1}(t_{m})=&x_{k}(t_{m})+v_{k},\end{array}}\right\}k=0,1,\ldots .}$

Compared to the simple method, only the first equation has been replaced.

The diagram shows that the starting error that the Newton steps (shown in green) have to bridge is usually much smaller than with the trivial predictor, with a smooth curve of the order of magnitude . This improvement actually only requires an insignificant additional effort, because the matrix corresponds to that from the Newton step. You can therefore reuse the last LR decomposition from Newton's method for calculating the tangent . ${\displaystyle O(h_{m}^{2})}$ ${\displaystyle D_{x}F{\big (}x(t_{m-1}),t_{m-1}{\big )}}$ ${\displaystyle x(t_{m-1})}$ ${\displaystyle z_{m-1}}$

In the practical implementation one tries to ensure the convergence of the Newton method by step size control . To do this, choose the step size so that the contraction in the first two Newton steps is sufficiently small, in particular less than one. If the selected one turns out to be too large and the Newton method converges poorly or not at all, repeat the step with a smaller one . ${\displaystyle h_{m}}$ ${\displaystyle h_{m}}$ ${\displaystyle t_{m-1}\to t_{m}=t_{m-1}+h_{m-1}}$ ${\displaystyle h_{m}}$

General curve tracking

The described methods only work without problems if the function F is differentiable enough often and the Jacobi matrix is regular everywhere . If the latter no longer applies, turning points and branch points of the curve can occur. ${\displaystyle D_{x}F}$

After turning points, the curve runs "backwards", at branch points it splits. In both cases, therefore, a (unique) parameterization according to the variable t is no longer possible. Therefore, one simply considers t as the -th component of the unknown and parameterizes the curve according to its arc length s . Then you look for all the solutions ${\displaystyle (n+1)}$ ${\displaystyle y=(x_{1},\ldots ,x_{n},t)^{T}}$

${\displaystyle y(s):\quad F(y(s))=0}$, in which ${\displaystyle F:\,\mathbb {R} ^{n+1}\to \mathbb {R} ^{n}}$

is. This system of equations is underdetermined and has an infinite number of solutions which, under suitable conditions, form a smooth solution curve . ${\displaystyle y(s)}$

As before, it follows from the chain rule that the tangent direction satisfies the homogeneous system of equations with the full Jacobian matrix, i.e. lies in the core of this matrix. So a predictor can be calculated again. The Newton method can also be carried out by choosing a direction that is orthogonal to the curve tangent, i.e. to the core of . This direction is calculated automatically by the Moore-Penrose pseudo inverse of . With this procedure, an approximation to the arc length s is increased step by step: ${\displaystyle F'(y(s))y'(s)\equiv 0}$ ${\displaystyle y'(s)}$ ${\displaystyle F'=\partial F/\partial y\in \mathbb {R} ^{n\times (n+1)}}$ ${\displaystyle F'(y)}$ ${\displaystyle F'}$

General predictor-corrector step

${\displaystyle {\begin{array}{rl}F'{\big (}y(s_{m-1}){\big )}z_{m-1}&=0,\ \|z_{m-1}\|_{2}=1,\\s_{m}&:=s_{m-1}+h_{m},\\y_{0}(s_{m})&:=y(s_{m-1})+h_{m}z_{m-1};\\y_{k+1}(s_{m})&:=y_{k}(s_{m})-{\Big (}F'(y_{k}(s_{m})){\Big )}^{+}\,F(y_{k}(s_{m})),\ k=0,1,\ldots .\end{array}}}$

The name denotes the mentioned pseudo-inverse . ${\displaystyle (\ldots )^{+}}$

The third diagram outlines this procedure, the Newton step (shown in green) runs approximately orthogonally to the curve and therefore has no problems at the reversal point (vertical course of the curve).

Remarks :

• The first condition does not yet determine the direction of the tangent . One chooses the sign of course so that the inner product is to proceed in one direction. ${\displaystyle \pm z_{m-1}}$ ${\displaystyle z_{m-1}^{T}z_{m-2}>0}$
• The two sub-steps can be carried out efficiently with the QR decomposition of the transposed matrix . The tangent direction can be obtained with any vector by normalizing if the last expression is not equal to zero. ${\displaystyle \,(F'(y))^{T}=QR}$ ${\displaystyle u\not =0}$ ${\displaystyle \,(E-QQ^{T})u}$
• The Newton correction is calculated using , where the vector solves the quadratic triangle system . ${\displaystyle \,v_{k}=y_{k+1}(s_{m})-y_{k}(s_{m})}$ ${\displaystyle v_{k}=-Q{\tilde {v}}_{k}}$ ${\displaystyle {\tilde {v}}_{k}\in \mathbb {R} ^{n}}$ ${\displaystyle R^{T}{\tilde {v}}_{k}=F(y_{k}(s_{m}))}$

literature

• Werner Rheinboldt: Numerical Analysis of Parametrized Nonlinear Equations. John Wiley and Sons, New York 1986, ISBN 0-471-88814-1 . (see also the FORTRAN module PITCON as part of the netlib.org library contin )
• P. Deuflhard, A. Hohmann: Numerical Mathematics. de Gruyter, 1991, ISBN 3-11-012917-5 .
• EL Allgower, K. Georg: Introduction to numerical continuation methods. SIAM Philadelphia, 2003, ISBN 0-89871-544-X .
• Schwetlick, H. and Kretschmar, H .: Numerical methods for natural scientists and engineers . Fachbuchverlag Leipzig, 1991, ISBN 3-343-00580-0 , p. 200 .