KTHNY theory

The KTHNY theory describes melting of crystals in two dimensions. The name comes from the first letters of the surnames of John Michael Kosterlitz and David J. Thouless or Bertrand Halperin , David R. Nelson and A. Peter Young , who developed the theory. In addition to the Ising model in 2D and the XY model in 2D, it is one of the few descriptions of phase transitions that can be solved analytically and that predicts transition temperatures . ${\displaystyle T>0}$

idea

The theory describes the dissociation of topological defects that destroy the order of the crystal. Michael Kosterlitz and David Thouless received the Nobel Prize in Physics in 2016 for using a renormalization group to describe how thermally excited virtual dislocations make the crystal increasingly soft when heated. The shear modulus disappears when they completely dissociate. David Nelson and Bertrand Halperin have shown that the resulting hexatic phase is not yet an isotropic liquid: the orientation order only disappears when a second class of topological defects, the disclinations, dissociate. Independently of this, Peter Young calculated the critical exponent of the diverging correlation length for the phase transition crystalline to hexatic.

The KTHNY theory predicts two continuous phase transitions , i.e. H. there is no latent heat and no phase coexistence occurs. The phases can be differentiated on the basis of their different discrete or continuous orders or symmetries with regard to translation and orientation. One phase transition separates the solid phase with quasi-long-range translation order and long-range orientation order from the hexatic phase, which has short-range translation order and quasi-long-range orientation order. The other phase transition separates the hexatic phase from the isotropic liquid, in which translation and orientation order are short-range. Since the energy differences between the respective thermodynamic phases disappear at the transition, the system is dominated by so-called critical fluctuations. This means that ordered and disordered areas fluctuate greatly in terms of space and time. The size of the areas increases very strongly in the vicinity of the respective phase transitions until they diverge at the transition temperature. At the phase transition, the patterns of the symmetry-broken areas show a fractal pattern compared to those of the high-symmetry phase . Fractals are length scale invariant; H. they look the same on any length scale or any enlargement factor (this applies to all scales greater than the interatomic distance). This scale invariance is the prerequisite for using the renormalization group to describe the phase transitions. In the transition from the high to the low temperature phase, spontaneous symmetry breaking occurs. In contrast to the melting and freezing of three-dimensional crystals, the symmetry breaks for translational and orientational symmetry do not have to occur at the same temperature, since the two types of topological defects can destroy the order at different temperatures.

background

Michael Kosterlitz and David Thouless tried in their work to resolve a contradiction about two-dimensional crystals: On the one hand, the Mermin-Wagner theorem says that there is no spontaneous symmetry breaking in two dimensions for continuous order parameters. For 2D crystals this means that there cannot be a perfect long-range periodicity. However, the first molecular dynamics simulations by Bernie Alder and Thomas E. Wainwright showed crystallization in 2D. The definition of a 2D crystal has been implicitly modified with the KTHNY theory, which predicts two symmetry breaks: Long-range periodicity is not a necessary criterion for a finite shear modulus, as amorphous solids already show. According to KTHNY theory, the existence of a shear modulus is sufficient to define a solid in 2D, which includes quasicrystals in the definition.

Structure factor

Structure factor of a) isotropic liquid, b) the hexatic phase, c) a crystal in two dimensions

The three different thermodynamic phases and their respective order states and symmetries can be identified with the structure factor

${\displaystyle S({\vec {q}})={\frac {1}{N}}\langle \sum _{ij}e^{-i{\vec {q}}({\vec {r}}_{i}-{\vec {r}}_{j})}\rangle }$

visualize. The double sum runs over all positions of the particle pairs i and j, the square brackets mean a time averaging over different configurations. In the isotropic liquid one sees concentric rings at , if the mean particle distance is obtained from the 2D particle density . In the crystalline phase one finds sixfold symmetry, which results from the long-range orientation order. Since the translation order is only quasi-long-range due to the Mermin-Wagner theorem , the peaks do not have any pointy shape ( peaks) as in 3D, but rather, according to theory, the shape of a Lorenz curve. The hexatic phase is characterized by six circular segments, which reflect the quasi-long-range orientation order. The structure factors in the figure are calculated from the positions of the particles from a monolayer of colloids (the crosses at high intensities are artifacts from the finite spatial (square) image section when calculating the Fourier transformation). ${\displaystyle q=2\pi /a}$ ${\displaystyle a=1/{\sqrt {\rho }}}$ ${\displaystyle \rho }$ ${\displaystyle \delta }$

Interaction of Dislocations

When the elastic modulus is reached, the elasticity disappears discontinuously and the crystal melts ${\displaystyle 16\pi }$

To analyze the melting of the crystal due to the dissociation of the dislocations, one starts from the energy as a function of the distance between two dislocations: ${\displaystyle H_{lok}}$

${\displaystyle H_{lok}=-{\frac {a^{2}E}{8\pi }}\sum _{k\neq l}{\Big [}{\vec {b}}({\vec {r}}_{k})\cdot {\vec {b}}({\vec {r}}_{l})\ln {\frac {\Delta {\vec {r}}_{k,l}}{a}}-{\frac {[{\vec {b}}({\vec {r}}_{k})\cdot \Delta {\vec {r}}_{k,l}][{\vec {b}}({\vec {r}}_{l})\cdot \Delta {\vec {r}}_{k,l}]}{\Delta r_{i,j}^{2}}}{\Big ]}+E_{c}\cdot N_{lok}}$

The double sum runs over all positions of pairs of defects and , measures the distance between the respective dislocations. is the Burgers vector and determines the orientation of the dislocation at the location . In this way, the second term in square brackets has the effect that dislocation pairs are preferably aligned antiparallel for energetic reasons. This term can be neglected for further calculations if the distances between the defects are large. The logarithmic term (first term in brackets) is important, which describes how the energy of a dislocation pair diverges with increasing distance. Because there is a shortest distance for Dislokationspaare given by the mean particle distance , the scaling of the Dislokationsabstandes prevented that may be negative. The strength of the interaction is proportional to the modulus of elasticity , which indicates the stiffness of the crystal lattice. In order for a dislocation pair to arise, the atoms need to be shifted slightly to one another, less than the mean particle distance . The associated discrete energy must be counted for each of the disclinations (last term). ${\displaystyle k}$ ${\displaystyle l}$ ${\displaystyle \Delta {\vec {r}}_{k,l}={\vec {r}}_{k}-{\vec {r}}_{l}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle {\vec {r}}_{k}}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle \ln {\frac {\Delta {\vec {r}}_{k,l}}{a}}}$ ${\displaystyle E}$ ${\displaystyle a}$ ${\displaystyle E_{c}}$ ${\displaystyle N_{lok}}$

A clear argument for the logarithmic term is that the magnitude of the distortion around an isolated dislocation decreases with increasing distance. In the Hook's approximation, strain is linear in elastic stress. The energy is obtained by integrating the voltage once, which provides the logarithm. The logarithmic distance dependence is the reason why the KTHNY theory is one of the few theories for phase transitions that can be solved analytically: In statistical physics, the partition function has to be calculated, i.e. H. the probability distribution for all possible configurations of dislocation pairs, given by a Boltzmann factor . Here is the thermal energy with the Boltzmann constant . For the majority of problems in statistical physics , the partition function cannot be solved because of the enormous number of particles / degrees of freedom. With the logarithmic energy function of the dislocations and the exponential function as an inverse function in the Boltzmann factor, this is different for the KTHNY theory. ${\displaystyle \propto {\frac {1}{r}}}$ ${\displaystyle e^{\frac {H_{lok}}{k_{B}T}}}$ ${\displaystyle k_{B}T}$ ${\displaystyle H_{lok}}$

example

The mean square of the distance between two dislocations is to be determined as an observable, whereby the interaction is simplified and only the dominant logarithmic term is considered:

${\displaystyle \langle r^{2}\rangle ={\frac {\int r^{2}\cdot e^{-{\frac {Ea\ln(r/a)}{4\pi k_{B}T}}}d^{2}r}{\int e^{-{\frac {Ea\ln(r/a)}{4\pi k_{B}T}}}d^{2}r}}\sim {\frac {2-{\frac {E\cdot a}{4\pi k_{B}T}}}{4-{\frac {E\cdot a}{4\pi k_{B}T}}}}}$

For low temperatures the square of the distance tends to zero , the dislocations annihilate and the crystal is free of defects. However, if the denominator becomes zero, this expression diverges . That happens when is. If the spacing of the dislocations diverges, it means that they are dissociated and no longer form a bonded pair. In this case the crystal is melted. The melting temperature is determined by the modulus of elasticity: ${\displaystyle \langle r^{2}\rangle \to 0}$ ${\displaystyle \langle r^{2}\rangle \to \infty }$ ${\displaystyle {\frac {E\cdot a}{4\pi k_{B}T}}=4}$ ${\displaystyle T_{m}}$

${\displaystyle {\frac {E\cdot a}{k_{B}T_{m}}}=16\pi }$

The dimensionless quantity represents a universal constant for melting in two dimensions and is completely independent of the type of system. The example here only considers an isolated pair of dislocations. In general, many dislocations will occur during melting and the elastic modulus will depend on the temperature. This feedback of the dislocations on the modulus of elasticity describes the renormalization group . ${\displaystyle 16\pi }$

Renormalization of elasticity

When the crystal is heated, local virtual dislocation pairs are created in the vicinity of the melting temperature due to thermal fluctuations . Virtual means that the mean thermal energy is not yet sufficient to dissociate the dislocations; however, for a short time they can arise locally before they annihilate again. Although they disappear again, they have a measurable effect on the elasticity, they make the crystal softer. The principle is completely analogous to the renormalization of the electrical charge in quantum electrodynamics, where virtual electron-positron pairs shield the naked charge of the electron / proton as a quantum fluctuation of the vacuum. Put clearly: If the crystal is softer due to the presence of virtual dislocations, the probability (fugacity) of new virtual dislocations increases, proportional to the Boltzmann factor of the discrete energy of a dislocation pair . If there are further virtual dislocations, they make the crystal softer, if the crystal is softer, the fugacity increases and so on…. David Nelson, Bertrand Halperin and independently Peter Young derived the recursion equations for fugacity and elasticity by using the renormalization group: the system is critical near the phase transition, which means that it is self-similar on all length scales . If a length scale transformation is now made by the factor and , the system must look identical, in particular the energy function of the dislocations must be form-invariant. After not only one pair of dislocations, but many mutually shielding dislocations (which make the system softer) are considered after a length scale transformation (in a larger section of the crystal), this additional softness is compensated for in the renormalized (reduced) elasticity. The recursion equation for the elasticity module and the fugacity are: ${\displaystyle y}$ ${\displaystyle y=e^{\frac {E_{C}}{k_{B}T}}}$ ${\displaystyle \gg a}$ ${\displaystyle l}$ ${\displaystyle E\to E(l)}$ ${\displaystyle y\to y(l)}$

${\displaystyle {\frac {dE^{-1}(l)}{dl}}={\frac {3}{2}}\pi y^{2}e^{E(l)/8\pi }I_{0}{\Big (}E(l)/8\pi {\Big )}-{\frac {3}{4}}\pi y^{2}e^{E(l)/8\pi }I_{1}{\Big (}E(l)/8\pi {\Big )}}$

${\displaystyle {\frac {dy(l)}{dl}}={\Big (}2-{\frac {E(l)}{8\pi }}{\Big )}y(l)+2\pi y^{2}e^{E(l)/16\pi }I_{0}{\Big (}E(l)/8\pi {\Big )}}$

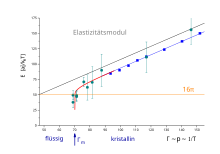
Analog recursion equations can be written for the shear modulus and the compression modulus, and are each Bessel functions . For different starting values, these recursion formulas run in two “directions”, means no defects, the system is crystalline and , meaning any number of defects, the system is fluid. The fixed point of the system delivers at , but now with the renormalized modulus of elasticity instead of the unrenormalized. In the figure, the modulus of elasticity is plotted as a function of the dimensionless coupling strength . is the ratio of the repulsive energy between two particles to the thermal energy (which was left constant in this experiment) and can be interpreted as pressure or inverse temperature. The black curve is a thermodynamic calculation of a perfect hexagonal crystal at . The blue curve is from computer simulations and shows a reduced modulus of elasticity due to lattice vibrations . The red curve is the renormalization according to the recursion equations, it drops off at zero. The turquoise points are measurements of the elasticity of a colloidal monolayer, they confirm the melting temperature at . ${\displaystyle I_{0}}$ ${\displaystyle I_{1}}$ ${\displaystyle y\to 0}$ ${\displaystyle y\to \infty }$ ${\displaystyle y=0}$ ${\displaystyle E_{R}/k_{B}T=16\pi }$ ${\displaystyle E_{R}}$ ${\displaystyle \Gamma }$ ${\displaystyle \Gamma }$ ${\displaystyle T=0}$ ${\displaystyle T>0}$ ${\displaystyle 16\pi }$ ${\displaystyle E_{R}=16\pi }$

Interaction of the disclinations

Frank's constant in the hexatic phase: it falls below on the transition to the isotropic liquid, and diverges on the transition to the 2D crystal ${\displaystyle 72/\pi }$

After dissociation of dislocations, the system is in the hexatic phase . In order to analyze the further melting of the hexatic phase into the isotropic liquid due to the dissociation of the disclinations, analogous considerations can be made. One starts with the energy as a function of the distance between two disclinations: ${\displaystyle H_{kli}}$

${\displaystyle H_{kli}=-{\frac {K_{A}\cdot \pi }{36}}\sum _{k\neq l}s({\vec {r}}_{k})\cdot s({\vec {r}}_{l})\ln {\frac {\Delta {\vec {r}}_{k,l}}{a}}+E_{s}\cdot N_{kli}}$

The logarithmic term of the distance between the individual disclinations is again dominant. The sign of the interaction, i.e. H. the attraction or repulsion is determined by the number of turns and the five- or seven-fold disclinations, so that 'charges' attract each other with different signs. The general strength of the interaction is set by the rigidity against twisting, called Frank's constant based on the theory of liquid crystals . is the discrete distortion energy that is necessary to turn one dislocation into two disclinations. Completely analog calculations can be made for the square of the distance between the disclinations, only the prefactor has to be replaced accordingly. It diverges when it is. If the disclinations are unbound, the system has passed from the hexatic phase into the isotropic liquid, the transition temperature is given by the Frank constant: ${\displaystyle +\pi /3}$ ${\displaystyle -\pi /3}$ ${\displaystyle F_{A}}$ ${\displaystyle E_{s}}$ ${\displaystyle {\frac {F_{A}\cdot \pi }{36}}=4}$ ${\displaystyle T_{m}}$

${\displaystyle {\frac {F_{A}}{k_{B}T_{i}}}=72/\pi }$

The constant is also a universal constant. The figure shows the measurement of the torsional stiffness of a colloidal monolayer; The Frank constant falls below this universal constant. ${\displaystyle 72/\pi }$ ${\displaystyle T_{i}}$

Critical exponents

Continuous phase transitions (those of the 2nd or higher order according to Ehrenfest notation ) show critical fluctuations in ordered and disordered areas in the vicinity of the phase transition. The appropriately chosen correlation lengths typically diverge algebraically in 3D with as transition temperature and as critical exponent. Another special feature of the Kosterlitz-Thouless transitions is that the correlation lengths of the translation and orientation correlation function (see hexatic phase ) diverge exponentially: ${\displaystyle \xi =\xi _{0}{\Big (}{\frac {T-T_{c}}{T_{c}}}{\Big )}^{-\nu }}$ ${\displaystyle T_{c}}$ ${\displaystyle \nu }$

${\displaystyle \xi =\xi _{0}\cdot e^{{\Big (}{\frac {T-T_{c}}{T_{c}}}{\Big )}^{-\nu }}}$

with the critical exponent for the divergence at the crystalline - hexatic transition according to renormalization group theory. D. Nelson and B. Halperin have predicted that the Frank constant also diverges exponentially with . The red curve in the figure shows an exponential fit of the critical behavior with . This value is compatible with the KTHNY theory within the framework of the error bars. The theory predicts the divergence at the hexatic - isotropic transition . This smooth value is compatible with molecular field theories (mean field theory) and means that no renormalization of the Frank constant is necessary, i.e. H. the increasing shielding of disclination pairs need not be considered - this has already been sufficiently taken over by dislocations, of which there are many. Experiments provided a value of . ${\displaystyle {\bar {\nu }}=0{,}36963\dots }$ ${\displaystyle T_{m}}$ ${\displaystyle {\bar {\nu }}}$ ${\displaystyle {\bar {\nu }}=0{,}35\pm 0{,}02}$ ${\displaystyle \nu =0{,}5}$ ${\displaystyle T_{i}}$ ${\displaystyle \nu =0{,}5\pm 0{,}03}$

Alternative theoretical models for two-dimensional melting were u. a. set up by ST Chui as well as MA Glaser and N. Clark. In contrast to the KTHNY theory, however, there is no hexatic phase here. The verification of the hexatic phase has been successful both experimentally and via computer simulations . For short-range particle interaction, simulations (deviating slightly from the KTHNY theory) for the hexatic - isotorp transition show that it is weak first order.

Individual evidence

1. ^ JM Kosterlitz, DJ Thouless: Long Range Order and Metastability in Two-Dimensional Solids and Superfluids . In: Journal of Physics C . 5, 1972, p. 124. doi : 10.1088 / 0022-3719 / 5/11/002 .
2. ^ JM Kosterlitz, DJ Thouless: Ordering Metastability, and Phase Transitions in Two-Dimensional Systems . In: Journal of Physics C . 6, No. 1181, 1973. doi : 10.1088 / 0022-3719 / 6/7/0102 .
3. ^ BI Halperin, DR Nelson: Theory of Two-Dimensional Melting . In: Physical Review Letters. . 41, 1978, p. 121. doi : 10.1103 / PhysRevLett.41.121 .
4. ^ DR Nelson, BI Halperin: Dislocation-mediated melting in two dimensions . In: Physical Review B . 19, 1979, p. 2457. doi : 10.1103 / PhysRevB.19.2457 .
5. ^ PA Young: Melting and the vector Coulomb gas in two dimensions . In: Physical Review B . 19, 1979, p. 1855. doi : 10.1103 / PhysRevB.19.1855 .
6. ^ JM Kosterlitz: The critical properties of the two-dimensional XY model . In: Journal of Physics C . 7, 1974, p. 1046. doi : 10.1088 / 0022-3719 / 7/6/005 .
7. ^ DR Nelson, JM Kosterlitz: Universal Jump in the Superfluid Density of Two-Dimensional Superfluids . In: Physical Review Letters . 39, 1977, p. 1201. doi : 10.1103 / PhysRevLett.39.1201 .
8. ^ M. Kosterlitz: Nobel Lecture 2016
9. ^ M. Kosterlitz: Commentary on Ordering, metastability and phase transitions in two-dimensional systems . In: Journal of Physics C . 28, 2016, p. 481001. doi : 10.1088 / 0953-8984 / 28/48/481001 .
10. ↑ U. Gasser, G. Maret, P. Keim Phase transitions through topological defects: The melting of two-dimensional crystals
11. ↑ J. Zanghellini, P. Keim, von Grünberg HH: The softening of two-dimensional colloidal crystals . In: J. Phys. Cond. Mat. . 17, No. 45, 2005, p. 3579. doi : 10.1088 / 0953-8984 / 17/45/051 .
12. ^ P. Keim, G. Maret, HH von Grünberg: Frank's constant in the hexatic phase . In: Physical Review E . 75, 2007, p. 031402. doi : 10.1103 / PhysRevE.75.031402 .
13. ↑ U. Gasser, C. Eisenmann, G. Maret, P. Keim: Melting of crystals in two dimensions - mini review . In: ChemPhysChem . 11, No. 5, 2010, p. 963. doi : 10.1002 / cphc.200900755 .
14. ↑ A. Jaster: The hexatic phase of the two-dimensional system hard disks . In: Physics Letters A . 330, 2004, p. 120. doi : 10.1016 / j.physleta.2004.07.055 .
15. ^ S. Kapfer, W. Krauth: Two-Dimensional Melting: From Liquid-Hexatic Coexistence to Continuous Transitions . In: Physical Review Letters . 114, 2015, p. 035702. doi : 10.1103 / PhysRevLett.114.035702 .