Communicating tubes

Hydrostatic paradox : the water level in communicating pipes is the same, regardless of their shape and course.

Animation for filling communicating tubes

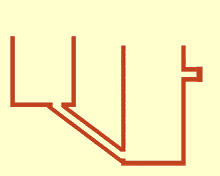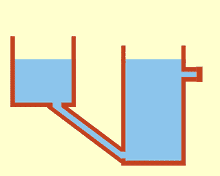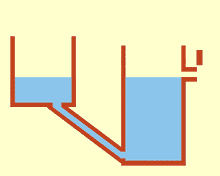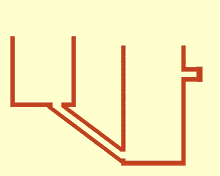
When communicating tubes or communicating vessels is called open at the top, but related bottom vessels . A homogeneous liquid is the same level in them because gravity and air pressure are constant.

The connection between the tubes can even be above the liquid level as long as the connecting line is completely filled with liquid and its connection to the vessels is below the liquid level. This principle is also used in the Hotopp siphon for emptying lock chambers . The filling of the "connecting pipe" or the drain pipe is brought about by negative pressure generated by a hydraulic piston ; this corresponds to the suction lifter principle .

A light liquid rises higher.

When different liquids are connected in tubes, the heights of the liquid columns are inversely proportional to their specific gravity , i.e. H. lighter liquids rise higher.

Schematic representation of a culvert

Applications and occurrences

The principle of communicating vessels is used for leveling devices to determine the horizontal , for example with the hose level and the sewer level , with which one can measure height differences to a fraction of a millimeter.

With the siphon , a form of suction pump, the liquid transfer is only stopped when the two liquid levels are equal. Siphons and culverts are water pipes going down and up again that can be used to bridge a depression. Water towers also use the principle of communicating tubes to create constant pressure in water pipes. With a culvert , fluids (mostly water) can be passed under obstacles or through a valley between mountains without building an aqueduct . The Romans used the principle for inner-city pressure lines.

If containers set up next to one another, such as rainwater tanks, are connected to one another by communicating pipes, this results in the same fill level in all containers , even if only a single container has an inlet or outlet. A large container can be replaced by a battery of smaller vessels.

A glass tube ( sight glass ) or a transparent hose connected near the bottom serves as a level indicator of a closed, opaque container , which is led upwards from there and shows its liquid level.

The tube centrifuge uses the different heights of rising liquids of different densities to separate liquid mixtures ( liquid-liquid separation ).

In the event of a flood, a wall or a dam can only stop the water if the foundation is such that there is no water flow in the ground. Otherwise the water level would be the same on both sides.

The water flows from an artesian well due to the pressure of the water column in the water-bearing soil layers. The water pressure can be used for water features and fountains .

Level surface and measuring accuracy

The communicating liquid level lies on a level or equipotential surface along which the earth's gravity potential is constant.

For accurate height measurements , disruptive effects must be avoided. This mainly includes vibrations in the system that cause the water level to fluctuate at both ends. Even small air pressure differences due to the influence of wind or temperature differences can have a noticeable effect depending on the type and length of the tubes . The capillary effect is noticeable in the case of very thin tubes or hoses .

If all these effects are precisely recorded or avoided by controlled conditions, height differences over distances of hundreds of meters can be measured with a deviation of 0.01 mm with precision hose levels. In this way, z. B. to understand a network of heights on both sides of a river more precisely than would be possible with measurements on an optical basis, since this results in the disruption of light refraction by the moisture contained in the air .

literature

E. Jochmann: Ground plan of the experimental physics. 1st edition, Salzwasser Verlag GmbH, Paderborn, ISBN 978-3-84600-754-9 .
Orest D. Chwolson, Gerhard Schmitt (ed.): The theory of the gaseous, liquid and solid bodies. Second improved and increased edition, Springer Fachmedien Wiesbaden GmbH, Wiesbaden 1913.
Alfred Böge, Wolfgang Böge: Technical Mechanics. Statics - Friction - Dynamics - Strength of Materials - Fluid Mechanics, 31st edition, Springer Fachmedien, Wiesbaden 2015, ISBN 978-3-658-09154-5 .

Web links

Video of communicating tubes
Communicating Tubes in Spectrum of Science (accessed September 1, 2016)
Uni Kassel Hydrostatics (accessed on September 1, 2016) Template: dead link /! ... nourl ( page no longer available )
Application of hydrostatic pressure (accessed on September 1, 2016) Template: dead link /! ... nourl ( page no longer available )
Operating Instructions Communicating Tubes (accessed September 1, 2016)

Remarks

↑ The maximum altitude is limited by air pressure and gravity. With an air pressure of , a gravitational acceleration of and a density of the liquid of , the maximum altitude is at most . From this height a vacuum would arise, but the liquid usually becomes gaseous beforehand. ${\ displaystyle p = 10 ^ {5} \, \ mathrm {Pa}}$ ${\ displaystyle g = 10 \, \ mathrm {\ tfrac {m} {s ^ {2}}}}$ ${\ displaystyle \ rho = 10 ^ {3} \, \ mathrm {\ tfrac {kg} {m ^ {3}}}}$ ${\ displaystyle h}$ ${\ displaystyle h = {\ tfrac {p} {g \ cdot \ rho}} = 10 \, \ mathrm {m}}$

↑ see also the graphic at Friedrich Engelhard: Canal and lock construction. Springer-Verlag, 2013, ISBN 978-3-709-19963-3 , p. 205 ( limited preview in Google book search).

[1] The maximum altitude is limited by air pressure and gravity. With an air pressure of , a gravitational acceleration of and a density of the liquid of , the maximum altitude is at most . From this height a vacuum would arise, but the liquid usually becomes gaseous beforehand. ${\ displaystyle p = 10 ^ {5} \, \ mathrm {Pa}}$ ${\ displaystyle g = 10 \, \ mathrm {\ tfrac {m} {s ^ {2}}}}$ ${\ displaystyle \ rho = 10 ^ {3} \, \ mathrm {\ tfrac {kg} {m ^ {3}}}}$ ${\ displaystyle h}$ ${\ displaystyle h = {\ tfrac {p} {g \ cdot \ rho}} = 10 \, \ mathrm {m}}$

[2] see also the graphic at Friedrich Engelhard: Canal and lock construction. Springer-Verlag, 2013, ISBN 978-3-709-19963-3 , p. 205 ( limited preview in Google book search).