Local structure
The local structure is a term from nuclear solid-state spectroscopy that describes the close vicinity of an atom with its neighboring atoms in crystals and molecules .
The atoms in crystals, for example, form very extensive, regular structures, the order of which is retained on a macroscopic scale, see Naica Cave . However, the lattice structure of crystals is not perfect, but contains defects. These are flaws at which an element of a lattice site is replaced by another element (substitution) or an atom (foreign or not foreign in the crystal) sits on an interstitial lattice. Vacancies are also possible where an atom is missing. Vacancies are of great importance for the diffusion in crystal lattices.
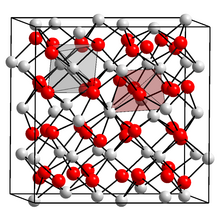
With the methods of nuclear solid-state spectroscopy it is possible to use the atomic nucleus as a probe and to measure the interactions hyperfine interaction of the atomic nucleus with the electric and magnetic local fields surrounding it. The atomic nucleus is much smaller than the atom, approx. 10,000–150,000 times smaller, so that the nucleus can be viewed almost as a point. The electric fields are created by the electrons in the atomic shell and are influenced by the closest neighboring atoms. In the above example of NaCl , each sodium atom is surrounded by 6 chlorine atoms, which form an octahedron around the sodium atom (more precisely sodium ion), see blue colored object. If all charges around the sodium atom are distributed symmetrically, which is usually the case in cubic crystal lattices, they cancel each other out at the nucleus. If this is not the case, the nucleus experiences a gradually changing field, see electric field gradient (EFG). The magnitude of EFG is about 10 21 V / m². The fields can be particularly large in the case of defects. Methods of nuclear solid-state spectroscopy such as B. Mössbauer spectroscopy or disturbed gamma-gamma angle correlation enable the direct measurement of the statistical distribution of EFG in a structure. In connection with calculations of the EFG with the density functional theory , improved models of the local structure can be created.
With magnetic materials, the same picture emerges as was just described, only that local magnetic fields are considered here.
Understanding the local structure plays a role in functional materials that are often determined by their defect chemistry. Areas of application can be found in ceramic electronic components, semiconductor materials, computer chips, batteries, solar cells or the many magnetic materials that z. B. be used in hard drives or in magnets .
Individual evidence
- ^ Kaufmann, Elton N; Reiner J. Vianden (1979). "The electric field gradient in noncubic metals". Reviews of Modern Physics. 51 (1): 161-214. doi: 10.1103 / RevModPhys.51.161 .
