Morphism (variety)

In algebraic geometry, a morphism of varieties is a mapping of varieties with certain regularity properties. An affine variety morphism is a polynomial map. Morphisms of affine varieties clearly correspond to homomorphisms of their coordinate rings . The definition can be generalized to quasi-affine, projective and quasi-projective varieties by locally defining morphisms with the help of regular functions.

Abstract variety morphisms are local sheaf morphisms.

(Note: The designation is not uniform in the literature. Sometimes the term regular mapping is also used for a morphism, not to be confused with regular functions .)

Definitions

Affine varieties

${\displaystyle \mathbb {A} _{k}^{n}}$denote the n- dimensional affine space over a body k.

A subset is an algebraic set if it is determined by an ideal : ${\displaystyle V\subset \mathbb {A} _{k}^{n}}$ ${\displaystyle I\subset k[x_{1},\ldots ,x_{n}]}$

${\displaystyle V=\{(x_{1},\ldots ,x_{n})|f(x_{1},\ldots ,x_{n})=0{\text{ für alle }}f\in I\}}$

An algebraic set is an affine variety if it cannot be written as a true union of two algebraic sets.

If and are algebraic sets or affine varieties, then a mapping is called ${\displaystyle V\subset \mathbb {A} _{k}^{n}}$ ${\displaystyle W\subset \mathbb {A} _{k}^{m}}$

${\displaystyle f\colon V\to W}$

Morphism, if there are polynomials , so for the mapping ${\displaystyle f_{1},\ldots ,f_{m}\in k[x_{1},\ldots ,x_{n}]}$

${\displaystyle F\colon \mathbb {A} _{k}^{n}\to \mathbb {A} _{k}^{m}}$

${\displaystyle F\colon (x_{1},\ldots ,x_{n})\mapsto (f_{1}(x_{1},\ldots ,x_{n}),\ldots ,f_{m}(x_{1},\ldots ,x_{n}))}$

holds that

${\displaystyle F|_{V}=f}$

An isomorphism is a bijective morphism whose inverse mapping is also a morphism. There are bijective morphisms that are not isomorphisms.

The morphisms from to form an algebra, the coordinate ring, which is denoted by. There is a canonical isomorphism ${\displaystyle V}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k[V]}$

${\displaystyle k(x_{1},\ldots ,x_{n})/I(V)\to k[V]}$

where the vanishing ideal of is: ${\displaystyle I(V)}$ ${\displaystyle V}$

${\displaystyle I(V):=\{f\in k[x_{1},\ldots ,x_{n}]|f(x_{1},\ldots ,x_{n})=0{\text{ für alle }}(x_{1},\ldots ,x_{n})\in V\}}$

Relation to algebra homomorphisms

Is a morphism ${\displaystyle \alpha }$

${\displaystyle \alpha \colon V\to W}$

then ${\displaystyle \alpha ^{*}}$

${\displaystyle \alpha ^{*}\colon k[W]\to k[V]}$

defined by

${\displaystyle \alpha ^{*}(f)=f\circ \alpha }$

a homomorphism of algebras. ${\displaystyle k}$

This assignment is a contravariant functor from the category of algebraic sets to the category of reduced -algebras of finite type. Every reduced algebra is isomorphic to one . The functor is an equivalence of categories . ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k[V]}$

The assignment is also a contravariant functor from the category of affine varieties to the category of zero- divisor - algebras of finite type. This is also an equivalence of categories. ${\displaystyle k}$

Affine, quasi-affine, projective and quasi-projective varieties

In order to extend the definition to quasi-affine, projective and quasi-projective varieties, regular functions are first defined in order to then define a morphism locally.

Regular functions

If it is a quasi-affine variety, then a function is regular at a point if there is an open neighborhood with and polynomials such that nowhere has zeros and ${\displaystyle Y\subset \mathbb {A} _{k}^{n}}$ ${\displaystyle f\colon Y\to k}$ ${\displaystyle P\in Y}$ ${\displaystyle U}$ ${\displaystyle P\in U}$ ${\displaystyle g,h\in k[x_{1},\ldots ,x_{n}]}$ ${\displaystyle h}$ ${\displaystyle U}$ ${\displaystyle f|_{U}={\frac {g}{h}}}$

Is a quasi-projective variety, then a function is regular at a point if there is an open neighborhood with and there are homogeneous polynomials with the same degree, so that nowhere has zeros and ${\displaystyle Y\subset \mathbb {P} _{k}^{n}}$ ${\displaystyle f\colon Y\to k}$ ${\displaystyle P\in Y}$ ${\displaystyle U}$ ${\displaystyle P\in U}$ ${\displaystyle g,h\in k[x_{0},x_{1},\ldots ,x_{n}]}$ ${\displaystyle h}$ ${\displaystyle U}$ ${\displaystyle f|_{U}={\frac {g}{h}}}$

${\displaystyle g}$and are not functions on that , but is a well-defined function since and are homogeneous of the same degree. ${\displaystyle h}$ ${\displaystyle \mathbb {P} _{k}^{n}}$ ${\displaystyle {\frac {g}{h}}}$ ${\displaystyle g}$ ${\displaystyle h}$

If a quasi-affine or a quasi-projective variety, then a function is regular if it is regular at every point in . ${\displaystyle Y}$ ${\displaystyle f\colon Y\to k}$ ${\displaystyle Y}$

If the body is identified with the affine space , then a regular function is continuous in the Zariski topology . (Conversely, however, not every continuous mapping is a regular function.) ${\displaystyle k}$ ${\displaystyle \mathbb {A} _{k}^{1}}$

Morphisms

In the following, and are affine, quasi-affine, projective or quasi-projective varieties. ${\displaystyle X}$ ${\displaystyle Y}$

These objects naturally carry a topology , namely the Zariski topology , in which the closed sets are exactly the algebraic sets.

A morphism from to is a continuous function that retrieves regular functions from to regular functions from . More accurate: ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \phi \colon X\to Y}$ ${\displaystyle Y}$ ${\displaystyle X}$

• A continuous function is a morphism if it holds for all open subsets that, if is a regular function, then is also regular on . ${\displaystyle \phi \colon X\to Y}$ ${\displaystyle V\subset Y}$ ${\displaystyle f\colon V\to k}$ ${\displaystyle f\circ \phi \colon \phi ^{-1}(V)\to k}$ ${\displaystyle \phi ^{-1}(V)}$

Rational illustration

→ Main article : Rational mapping

A rational mapping is a morphism from an open set to , so that has no continuation on a proper superset of . Is , is called in regularly . A morphism is therefore also called a regular mapping. ${\displaystyle \phi }$ ${\displaystyle U\subset X}$ ${\displaystyle Y}$ ${\displaystyle \phi }$ ${\displaystyle Y}$ ${\displaystyle x\in U}$ ${\displaystyle \phi }$ ${\displaystyle x}$

Examples

Neil's parable

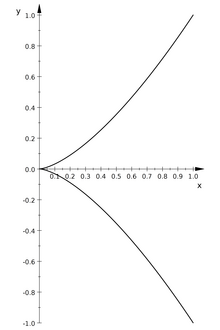
Neil's parabola in the affine real plane

An isomorphism is bijective and a homeomorphism , but a bijective homeomorphism is not necessarily an isomorphism: Is the semicubical parabola , ${\displaystyle X}$

${\displaystyle X:=\{(x,y)\in \mathbb {A} _{k}^{2}|\ y^{2}=x^{3}\}}$

so is the picture

${\displaystyle f\colon \mathbb {A} _{k}^{1}\to X}$

${\displaystyle f\colon (x)\mapsto (x^{2},x^{3})}$

a bijective homeomorphism that is not an isomorphism since the inverse mapping is not a morphism.

Quasi-affine varieties

It is not always possible to define morphisms of quasi-affine varieties by restricting their affine major variety, since not every morphism of a quasi-affine variety is a restriction of a morphism of the major variety. The variety is quasi-affine. The morphism: ${\displaystyle Y=A_{k}^{1}\setminus \{0\}}$

${\displaystyle f\colon Y\to Y}$

${\displaystyle f\colon x\mapsto {\frac {1}{x}}}$

is an isomorphism for which there is no morphism with ${\displaystyle g\colon A_{k}^{1}\to A_{k}^{1}}$ ${\displaystyle g_{|Y}=f}$

It applies

${\displaystyle Y\subsetneq A_{k}^{1}\subsetneq P_{k}^{1}}$ and

${\displaystyle Y\cup \{0\}=A_{k}^{1}}$

${\displaystyle A_{k}^{1}\cup \{\infty \}=P_{k}^{1}}$

For morphism with , so and , on the other hand, applies . ${\displaystyle g\colon P_{k}^{1}\to P_{k}^{1}}$ ${\displaystyle (x:y)\mapsto (y:x)}$ ${\displaystyle 0\mapsto \infty }$ ${\displaystyle \infty \mapsto 0}$ ${\displaystyle g_{|Y}=f}$

An isomorphism from to an affine variety can be given. It is an irreducible polynomial in general and ${\displaystyle Y}$ ${\displaystyle h\in k[x_{1},\ldots ,x_{n}]}$

${\displaystyle A_{k}^{n}\setminus V(f)=\{(x_{1},\ldots ,x_{n})\in A_{k}^{n}|f(x_{1},\ldots ,x_{n})\neq 0\}}$

the corresponding quasi-affine variety, also the hypersurface ${\displaystyle X\subset A_{k}^{n+1}}$

${\displaystyle X:=\{(x_{1},\ldots ,x_{n+1})\in A_{k}^{n+1}|x_{n+1}f(x_{1},\ldots ,x_{n})=1\}}$

so is the picture

${\displaystyle \phi \colon X\to A_{k}^{n}\setminus V(f)}$

${\displaystyle \phi \colon (x_{1},\ldots ,x_{n+1})\mapsto (x_{1},\ldots ,x_{n})}$

an isomorphism.

If, however, a sub-variety of codimension greater than 1 is removed from an affine variety, then this variety is not affine.

Images of morphisms

Images of quasi-projective varieties under morphisms are generally not quasi-projective varieties. If one looks at the morphism, for example

${\displaystyle f\colon A_{k}^{2}\to A_{k}^{2},(x,y)\mapsto (x,xy),}$

so you get as a picture . This is not a locally closed set in . However, the image is always a constructible set . In general, morphisms map constructible sets to constructible sets. ${\displaystyle f(A_{k}^{2})=\{(0,0)\}\cup \{(x,y)\in A_{k}^{2}\mid x\neq 0\}}$ ${\displaystyle A_{k}^{2}}$

Individual evidence

1. ^ Harris, Joe: Algebraic geometry. A first course. Corrected reprint of the 1992 original. Graduate Texts in Mathematics, 133. Springer-Verlag, New York, 1995. ISBN 0-387-97716-3
2. ^ Joe Harris : Algebraic Geometry. A first course. Springer, New Your 1992, ISBN 3-540-97716-3 , Theorem 3.16.

literature

• Brüske, Ischebeck, Vogel: Commutative Algebra , Bibliographisches Institut (1989), ISBN 978-3411140411
• Klaus Hulek: Elementary Algebraic Geometry . Vieweg, Braunschweig / Wiesbaden 2000, ISBN 3-528-03156-5 .
• Robin Hartshorne : Algebraic Geometry , Springer-Verlag, New York / Berlin / Heidelberg 1977, ISBN 3-540-90244-9