Polylogarithm

The polylogarithm is a special function created by the series

${\displaystyle \operatorname {Li} _{s}(z)=\sum _{k=1}^{\infty }{\frac {z^{k}}{k^{s}}}}$

is defined. For the polylogarithm changes to the ordinary logarithm : ${\displaystyle s=1}$

${\displaystyle \operatorname {Li} _{1}(z)=-\ln(1-z)}$

In the cases and one speaks accordingly of dilogarithm or trilogarithm. The definition applies to complex and with . This definition can be extended to further ones by analytical continuation . ${\displaystyle s=2}$ ${\displaystyle s=3}$ ${\displaystyle s}$ ${\displaystyle z}$ ${\displaystyle |z|<1}$ ${\displaystyle z}$

In the most important use cases is a natural number . For these cases one can use the polylogarithm recursively ${\displaystyle s=n}$

${\displaystyle \operatorname {Li} _{0}(z)={\frac {z}{1-z}}}$

${\displaystyle \operatorname {Li} _{n}(z)=\int _{0}^{z}{\frac {\operatorname {Li} _{n-1}(t)}{t}}\,{\text{d}}t\quad {\mbox{für}}\quad n=1,2,3,\dotsc }$

define according to which the dilogarithm is an integral of the logarithm, the trilogarithm an integral of the dilogarithm and so on. For negative integer values ​​of , the polylogarithm can be expressed using rational functions . ${\displaystyle s}$

The polylogarithm appears, for example, in connection with the Fermi-Dirac distribution and the Bose-Einstein distribution . In addition, it can be used to calculate any number of polylogarithmic constants (e.g. ) individually in the hexadecimal number system . ${\displaystyle \pi }$

Function values ​​and recursions

Graphs of some integer polylogarithms

Some explicit function terms for special integer values ​​of : ${\displaystyle s}$

${\displaystyle \operatorname {Li} _{1}(z)=-\ln \left(1-z\right)}$

${\displaystyle \operatorname {Li} _{0}(z)={\frac {z}{1-z}}}$

${\displaystyle \operatorname {Li} _{-1}(z)={\frac {z}{(1-z)^{2}}}}$

${\displaystyle \operatorname {Li} _{-2}(z)={\frac {z(1+z)}{(1-z)^{3}}}}$

${\displaystyle \operatorname {Li} _{-3}(z)={\frac {z(1+4z+z^{2})}{(1-z)^{4}}}}$

${\displaystyle \operatorname {Li} _{-4}(z)={\frac {z(1+z)(1+10z+z^{2})}{(1-z)^{5}}}}$

Formally, one can define with the (for all diverging) series . Although this series does not converge, this definition can be used to prove functional equations (in the ring of formally defined Laurent series ). ${\displaystyle \operatorname {Li} _{-n}(z):=\left(z{\frac {\text{d}}{{\text{d}}z}}\right)^{n}H(z)}$ ${\displaystyle z}$ ${\displaystyle H(z)=\sum _{k=-\infty }^{\infty }z^{k}}$

For all integer non-positive values ​​of , the polylogarithm can be written as a quotient of polynomials. So in these cases it is a rational function . For the three smallest positive values ​​of , the function values are given below: ${\displaystyle s}$ ${\displaystyle s}$ ${\displaystyle 1/2}$

${\displaystyle \operatorname {Li} _{1}\left({\tfrac {1}{2}}\right)=\ln 2}$

${\displaystyle \operatorname {Li} _{2}\left({\tfrac {1}{2}}\right)={\tfrac {1}{12}}\left(\pi ^{2}-6\,\ln ^{2}2\right)}$

${\displaystyle \operatorname {Li} _{3}\left({\tfrac {1}{2}}\right)={\tfrac {1}{24}}\left(4\,\ln ^{3}2-2\pi ^{2}\,\ln 2+21\,\zeta (3)\right)}$

${\displaystyle \zeta }$is the Riemann zeta function . No such formulas are known for larger values. ${\displaystyle s}$

It applies

${\displaystyle \operatorname {Li} _{s}(1)=\zeta (s)}$

and

${\displaystyle \operatorname {Li} _{s}(-1)=-\eta (s)}$

with the dirichletschen function ${\displaystyle \eta }$ .

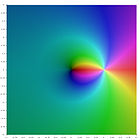
Different polylogarithmic functions in the complex plane

${\displaystyle \operatorname {Li} _{-3}(z)}$	${\displaystyle \operatorname {Li} _{-2}(z)}$	${\displaystyle \operatorname {Li} _{-1}(z)}$	${\displaystyle \operatorname {Li} _{0}(z)}$
${\displaystyle \operatorname {Li} _{1}(z)}$	${\displaystyle \operatorname {Li} _{2}(z)}$	${\displaystyle \operatorname {Li} _{3}(z)}$

Derivation

The derivation of the polylogarithms are again polylogarithms:

${\displaystyle {\frac {\text{d}}{{\text{d}}x}}\operatorname {Li} _{n}(x)={\frac {1}{x}}\operatorname {Li} _{n-1}(x)}$

Integral representation

The polylogarithm can be used for all complex ones ${\displaystyle z,s}$

${\displaystyle \operatorname {Li} _{s}(z)={\frac {z}{2}}+\ln ^{s-1}\,{\frac {1}{z}}\,\Gamma (1-s,-\ln \,z)+2z\int \limits _{0}^{\infty }{\frac {\sin(s\arctan t-t\,\ln \,z)}{(1+t^{2})^{s/2}(\mathrm {e} ^{2\pi \,t}-1)}}\,{\text{d}}t}$

with the help of the integral expression for Lerch's zeta function . It is the incomplete gamma function of the lower limit. ${\displaystyle \Gamma (s,z)=\int \limits _{z}^{\infty }t^{s-1}\mathrm {e} ^{-t}\,{\text{d}}t}$

Generalizations

Multi-dimensional polylogarithms

The multi-dimensional polylogarithms are defined as follows:

${\displaystyle \operatorname {L} _{a_{1},\dotsc ,a_{m}}(z)=\sum _{n_{1}>\dotsb >n_{m}>0}{\frac {z^{n_{1}}}{n_{1}^{a_{1}}\dotsb n_{m}^{a_{m}}}}}$

Lerch's zeta function

The polylogarithm is a special case of the transcendent Lerch's zeta function :

${\displaystyle \operatorname {Li} _{s}(z)=z\cdot \Phi (z,s,1)}$

Nielsen's generalized polylogarithms

Nielsen found the following generalization for the polylogarithm:

${\displaystyle \operatorname {S} _{n,p}(z)={\frac {(-1)^{n+p-1}}{(n-1)!p!}}\int \limits _{0}^{1}{\frac {\left(\ln(t)\right)^{n-1}\left(\ln(1-zt)\right)^{p}}{t}}{\text{d}}t}$

The following applies:

${\displaystyle \operatorname {S} _{n-1,1}(z)=\operatorname {Li} _{n}(z)}$

See also

• Fermi-Dirac integral

literature

• Alexander Goncharov : Polylogarithms in arithmetic and geometry. (PDF) In: Proceedings of the International Congress of Mathematicians (Zurich, 1994). Birkhäuser, Basel 1995, Vol. 1, 2, pp. 374-387.
• Milton Abramowitz , Irene Stegun : Handbook of Mathematical Functions . Dover Publications, New York 1964, ISBN 978-0-486-61272-0 , para. 27.7.

Web links

• Eric W. Weisstein : dilogarithm, trilogarithm and polylogarithm. In: MathWorld (English).
• David H. Bailey, David J. Broadhurst: A seventeenth-order polylogarithm ladder. arxiv : math.CA/9906134

Individual evidence

1. ↑ Eric W. Weisstein : Dirichlet Eta Function . In: MathWorld (English).
2. ↑ Eric W. Weisstein : Multidimensional Polylogarithms . In: MathWorld (English).
3. ↑ Eric W. Weisstein : Nielsen Generalized Polylogarithm . In: MathWorld (English).