premise

Example from syllogism

A premise ( Latin praemissa "that which has been sent ahead") or antecedent is a requirement or assumption in logic . It is a statement from which a logical conclusion is drawn.

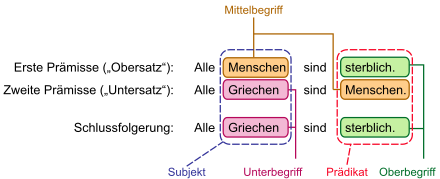
Example:

From "All Men Are Mortal"

and "All Greeks are human"

follows "All Greeks are mortal".

The first two statements are the premises, the last statement is the conclusion or conclusion.

Premises and truth

If the premises are true in a valid conclusion, the conclusion must be true too. An example of this is the above-mentioned conclusion that “All people are mortal” and “Socrates is a person” follows “Socrates is mortal”. However, the reverse is not true: if the premises (or some of the premises) are wrong, the conclusion is not necessarily wrong. For example, “All people are Greek” and “Socrates is a person” results in the sentence “Socrates is Greek”. One premise is wrong here, yet the conclusion is true.

So premises do not necessarily have to be true. On the contrary, one occasionally sets premises that are known to be completely wrong. This is e.g. B. the case with the proof technique of indirect proof , in which a false assumption is assumed with the aim of refuting it. Perhaps the best known example of an indirect proof is Euclid's theorem , which proves that there are infinitely many prime numbers .

History of philosophy

The term “premise” goes back to the Latin translation of Arabic literature into Aristotelian syllogistics in the 12th century. “Premise” is the translation of the ancient Greek word πρότασις ( protasis , “sent ahead ”). “Premise” are both precedents of a syllogism .

Symbolic illustration

Symbolically, a conclusion is represented as follows:

{\ displaystyle \ {\ mathrm {A} _ {1}, \ mathrm {A} _ {2}, \ ldots, \ mathrm {A} _ {n} \} \ vdash \ mathrm {B}}

Read: From it follows . ${\ displaystyle \ mathrm {A} _ {1}, \ mathrm {A} _ {2}, \ ldots, \ mathrm {A} _ {n}}$ ${\ displaystyle \ mathrm {B}}$

A conclusion can therefore have several premises; however, it is usually assumed to have only one conclusion. But this is basically convention, there is no fundamental reason why one conclusion should not have multiple conclusions.

Dependence and freedom from premises

The conclusion presented above is said to be that the conclusion follows from the premises . This does not mean that the conclusion is actually true or always has to be true; nor does it mean that the conclusion could only be true if the premises were true. Rather, it simply means that provided that all premises are true, the conclusion is also necessarily true. ${\ displaystyle \ mathrm {B}}$ ${\ displaystyle \ mathrm {A} _ {1}, \ mathrm {A} _ {2}, \ ldots, \ mathrm {A} _ {n}}$

In many logical systems, such as classical propositional and predicate logic , the deduction theorem applies . It states that it is permissible to shift one of the premises in the form of the antecedent of an “if-then” construction (technically called material implication or conditional) into the conclusion, i.e. from the argument:

{\ displaystyle \ {\ mathrm {A} _ {1}, \ mathrm {A} _ {2}, \ ldots, \ mathrm {A} _ {n} \} \ vdash \ mathrm {B}}

move on to the argument:

{\ displaystyle \ {\ mathrm {A} _ {1}, \ mathrm {A} _ {2}, \ ldots, \ mathrm {A} _ {n-1} \} \ vdash \ mathrm {A} _ { n} \ supset \ mathrm {B}}

Here, the former premise A _n became the antecedent, the former conclusion B the suffix of the conditional (read: "If A _n , then B"), which forms the conclusion of the new argument. ${\ displaystyle \ mathrm {A} _ {n} \ supset \ mathrm {B}}$

The calculus of natural inference is based on the deduction theorem .

example: Instead of inferring from "All people are mortal" and "Socrates is a person": "Socrates is mortal", one can deduce from "All people are mortal" alone: "If Socrates is a person, then he is mortal".

Another possibility of reducing the number of premises without affecting the validity of the argument arises if one of the premises can be derived from the others, i.e. if:

{\ displaystyle \ {\ mathrm {A} _ {1}, \ mathrm {A} _ {2}, \ ldots, \ mathrm {A} _ {n-1} \} \ vdash \ mathrm {A} _ { n}}

In this case the premise is superfluous (technical language: dependent) and can also be deleted from the set of assumptions. ${\ displaystyle \ mathrm {A} _ {n}}$

example: If it is possible to prove that Socrates is a human being, I can infer directly from "All human beings are mortal" that "Socrates is mortal" "

literature

Gottfried Gabriel : premise . In: Joachim Ritter ua (Hrsg.): Historical dictionary of philosophy . Volume 7, Schwabe, Basel 1972, Sp. 1255-1256

Web links

Wiktionary: premise - explanations of meanings, word origins, synonyms, translations

Individual evidence

^ Aristotle, Topic I, 10.
↑ Gottfried Gabriel : Premise . In: Joachim Ritter ua (Hrsg.): Historical dictionary of philosophy . Volume 7, Schwabe, Basel 1972, Sp. 1255–1256, here: p. 1255.

[1] Aristotle, Topic I, 10.

[2] Gottfried Gabriel : Premise . In: Joachim Ritter ua (Hrsg.): Historical dictionary of philosophy . Volume 7, Schwabe, Basel 1972, Sp. 1255–1256, here: p. 1255.