Kirchhoff's theorem

The Kirchhoff Theorem (also Kirchhoff-Trent Theorem , or Matrix-Scaffold Theorem ) is a theorem from the mathematical field of graph theory , which is named after Gustav Kirchhoff . The theorem states that the number of labeled spanning trees in a graph can be calculated in polynomial time using the determinant of a matrix obtained from the graph .

statement

The number of spanning trees in a graph corresponds to a cofactor of its Laplace matrix . The Laplacian matrix of a graph is obtained by starting from the Valenzmatrix ( diagonal matrix of node degrees ), the adjacency matrix is subtracted. A cofactor is the determinant of a sub-matrix obtained by deleting a row and a column. All cofactors of the Laplacian matrix provide the same value.

The cofactors of the Laplace matrix can be expressed in terms of their eigenvalues . The equivalent formulation is that the number of spanning trees in a graph is the same

${\displaystyle {\frac {1}{n}}\lambda _{1}\lambda _{2}\cdots \lambda _{n-1}}$

where are the eigenvalues ​​of the graph's Laplacian matrix that are not zero. ${\displaystyle \lambda _{1},\ldots ,\lambda _{n-1}}$

example

A graph with 4 nodes and all of its 8 spanning trees.

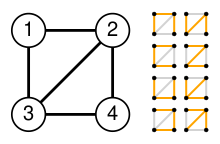
We consider the complete graph with 4 nodes in which 1 edge has been removed (as in the picture on the right). The Laplace matrix L of the graph results from the difference between the valence matrix and the adjacency matrix as follows:

${\displaystyle L=\left({\begin{array}{rrrr}2&0&0&0\\0&3&0&0\\0&0&3&0\\0&0&0&2\end{array}}\right)-\left({\begin{array}{rrrr}0&1&1&0\\1&0&1&1\\1&1&0&1\\0&1&1&0\end{array}}\right)=\left({\begin{array}{rrrr}2&-1&-1&0\\-1&3&-1&-1\\-1&-1&3&-1\\0&-1&-1&2\end{array}}\right).}$

The number of spanning trees is now obtained by deleting any row and column of L and then determining the determinant from this matrix. When deleting the first row and column you get:

Number of spanning trees ${\displaystyle =\det \left({\begin{array}{rrr}3&-1&-1\\-1&3&-1\\-1&-1&2\end{array}}\right)=8.}$

Generalizations

Kirchhoff's theorem can be generalized to weighted graphs with edge weight function w . In this case, the Laplace matrix L results from the weighted adjacency matrix multiplied by −1, in which the diagonal elements have been adjusted so that the entries in each row add up to zero. Let S be the set of spanning trees in G , then every cofactor of L corresponds ${\displaystyle G=(V,E,w)}$

${\displaystyle \displaystyle \sum _{T\in S}\,\prod _{e\in T}w(e)}$.

This method can be used to determine spanning trees in graphs with multiple edges . To do this, the multiple edges in G are deleted and the weighting function w is chosen so that it indicates the original multiplicity of the edges. Each spanning tree T in the graph weighted in this way corresponds to spanning trees in the multigraph. Accordingly, the cofactor of the Laplace matrix of the weighted graph corresponds to the number of spanning trees in the multigraph. ${\displaystyle \textstyle \prod _{e\in T}w(e)}$

Applications

With the help of Kirchhoff's theorem, the Cayley formula can be proven, which says that there are labeled trees with n nodes. The number of all trees with n nodes corresponds to the number of spanning trees of the complete graph with n nodes, i.e. according to Kirchhoff's theorem, the product of all eigenvalues ​​of the matrix ${\displaystyle n^{n-2}}$

${\displaystyle L_{n}:={\begin{pmatrix}n-1&-1&\cdots &-1\\-1&n-1&\cdots &-1\\\vdots &\vdots &\ddots &\vdots \\-1&-1&\cdots &n-1\\\end{pmatrix}},}$

that are not zero divided by n . The matrix has an eigenvalue 0 because the rank of the matrix is n -1. Furthermore, all vectors that have a 1 at one point, a −1 at the following point and otherwise only zeros are eigenvectors with the associated eigenvalues n . Since these n -1 vectors are linearly independent , the remaining n-1 eigenvalues ​​are accordingly n . It follows that the complete graph with n nodes has spanning trees. ${\displaystyle L_{n}}$ ${\displaystyle n^{n-2}}$

literature

• Lutz Volkmann: Foundations of the graph theory. Springer Verlag Vienna New York, Vienna 1996, ISBN 978-3-211-82774-1 .
• Lutz Volkmann: Graphs and Digraphs. An introduction to graph theory, Springer Verlag Vienna New York, Vienna 1996, ISBN 978-3-211-82267-8 .

Web links

• Algebraic Graph Theory (accessed October 29, 2015)
• Example for the matrix scaffolding set (accessed October 29, 2015)