Apparent size
The apparent size (also apparent diameter , visual angle , face angle , astronomical often angular extent ) of an object is the angle at which it is perceived by an observer.
The figure on the right illustrates the relationship between the apparent size α, distance r and the true extent g of an object. The following relationship between the three quantities can be derived from this:
- and thus for the angle
In geodesy , the distance can be calculated from the apparent size by means of an object with a standardized size, for example a vertically set up staff:
In astronomy , if the distance of an object is known, its approximate true extent across the line of sight is obtained
For small angles <1 °, the small-angle approximation applies , in radians : so that in angular minutes the following applies:
- .
With α = 1 ° the error is only 0.4 "(1.7 · 10 −6 rad or 0.001%), with α = 6 '= 0.1 ° only 0.004" (2 · 10 −9 rad or 0 , 0001%).
For a spherical object , the diameter of which is g and the distance to the center of the sphere r , the different formula applies because in the triangle the right angle is not at the center, but at the point of contact of the tangent. The difference disappears for small angles.
Vertical and horizontal viewing angle
In photography , one uses the vertical and horizontal viewing angles of an object. The vertical angle of vision ε v of an object is defined by circumscribing a horizontally lying rectangle around the object fixed by the eye, then drawing the two rays emanating from the eye to the end points of the vertical line through the center of the rectangle and determining the angle between these rays. Similarly, the horizontal viewing angle ε h is the angle between the two rays from the eye to the end points of the horizontal line through the center of the rectangle.
If you choose the Cartesian coordinate system whose origin lies in the center of the rectangle, whose y and z axes form the vertical and horizontal symmetry axes of the rectangle and where the viewer is in the half-space x> 0, these two viewing angles can be used for the Trigonometrically determine a rectangle with the vertical side length G v = 2γ v and the horizontal side length G h = 2γ h for any observer point (x, y, z):
- ,
- .
Due to the rotational symmetry of the function graph of the vertical viewing angle ε v (x, y, z) when rotating around the y-axis (cylindrical symmetry ), its investigation can be restricted to the x, y-plane. The following terms and the function graphs shown in the figures are obtained for the visual angle functions as functions of only the plane coordinates x and y:
- ,
Maximum viewing angle of an object for a camera
The camera location is restricted to an admissibility range Z for the complete and sharp imaging of a permanently specified object by means of a camera. This area Z is described by four inequalities in which the camera parameters are included:
- ε v (x, y, z) ≤ α v ,
- ε h (x, y, z) ≤ α h ,
- ρ (x, y, z) = ≥ d = g min - f,
- x> 0,
where α v is the vertical angle of view, α h is the horizontal angle of view, g min is the minimum object distance and f is the fixed focal length of the camera.
If one looks for a location in this area Z in which the vertical viewing angle ε v or the horizontal viewing angle ε h of the object is at a maximum for the camera, this provides a non-linear optimization problem, its objective function through the viewing angle to be maximized and its admissibility range Z is given. If, on the other hand, you want to find a location for a camera mounted on a camera crane in which both the vertical and the horizontal viewing angle are maximal, this leads to the solution of the maximization problem, in which both viewing angles are maximized simultaneously as target functions ("multi-criteria optimization") ).
If one restricts oneself to the x, y-plane with the simultaneous maximization of both viewing angles ε v and ε h , then the edge of the admissibility area Z is formed by two of the following three arcs:
- K d
- ,
- K h
- ,
- K v
- ,
with η h = γ h / tan (α h / 2), w v = tan α v , x v = γ v / w v , r v = γ v • (1 + w v 2 ) 1/2 , ξ v = x v + r v = γ v / tan (α v / 2), 0 <α h , α v <π.
The three cases I) 0 <α v <π / 2, II) α v = π / 2, III) π / 2 <α v <are used to determine the optimum range O s of the simultaneous maximization of both viewing angles ε v and ε h π and to differentiate between the subcases, how the radius R: = max {d, η h } lies with the other two parameters γ v and ξ v . In case I) with γ v <ξ v these are the subcases 1) R ≤ γ v , 2) γ v <R <ξ v and 3) R ≥ ξ v . For example, in case I.2), which mainly occurs in practice and shown in the figure, the optimality range O s consists of the two intersection points S = (x *, y *) and Ŝ = (x *, - y *) of the circular arcs K. R and K v .
Examples
| example | Angle of view in degrees (sorted by maximum) | Arc minutes | Size comparison (picture) |
|---|---|---|---|
| Entire field of view of the healthy human eye | 130 ° -150 ° | ||
| Seen from the surface of the earth, a rainbow occupies a maximum of a semicircle. | 84 ° × 42 ° |
 Rainbow with 18mm wide-angle lens . Rainbow with 18mm wide-angle lens .
|
|
| Your own fist with your thumb stretched out on your arm | approx. 10 ° |
|
|
| Andromeda Galaxy (photographic) | approx. 3 ° | 186.2 ′ |
 Photo montage for size comparison with the moon Photo montage for size comparison with the moon
|
| the width of your own thumb on the outstretched arm | 1.5-2 ° | ||
| the area of keen vision in humans | approx. 1 ° | ||
| The diameter of the full moon or the solar disk as seen from the earth. | approx. 0.5 ° | approx. 32 ′ |
 Apparent size of the sun and moon in comparison Apparent size of the sun and moon in comparison
|
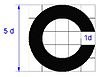
| The diameter of the Landolt ring for a vision of 50% | 10 ′ |
|
|
| Horsehead Nebula | approx. 8 ′ | ||
| Edge length of the Hubble Ultra Deep Field | approx. 3 ′ |

|
|
| Tennis ball 100 m away | approx. 2.5 ′ | ||
| Venus in lower conjunction | 1.1 ′ |
 Venus transit Venus transit
|
|
| Jupiter | 29.8–50.1 ″ ( arc seconds ) |

|
|
| International space station | 0.75 ′ = 45 ″ |

|
|
| For comparison: the resolution of the naked human eye under ideal conditions | 0.5 ′ to 1 ′ | ||
| Saturn | 18.5 ″ |
 Saturn compared to the moon in an occultation Saturn compared to the moon in an occultation
|
|
| Mars | 13.9–24.2 ″ |

|
|
| Mercury | 4.5-13.0 ″ |
 Mercury transit before the sun Mercury transit before the sun
|
See also
- Theorem of rays
- Angle of view
- Field of view
- Mock giant , literary play with the concept
- Forced perspective , a photographic stylistic device that deliberately exploits the human perception of size
literature
- Franz Pleier: The ideal location for a photographer . W seminar paper at Kepler-Gymnasium Weiden / OPf., 2010
Individual evidence
- ↑ angle of view. In: Digital dictionary of the German language . Retrieved September 3, 2019
- ↑ angle of view . Duden
- ↑ simbad.u-strasbg.fr
- ↑ baader-planetarium.de























