Self-locking

In mechanics, self-locking describes the resistance caused by friction against slipping or twisting of two bodies lying against one another. As soon as the static friction is exceeded, the bodies are no longer self-locking.
Self-locking is influenced by the angle of inclination , the surface roughness of the bearing surfaces, the material pairing, the lubricant and the heating. To achieve self-locking, the resulting angle is made smaller than the arctangent of the coefficient of static friction . This system is not exposed to any dynamically changing external stresses caused by vibrations .
Screw connections
In the case of screws, there is static self-locking if the pitch angle of the thread flank is smaller than the arctangent of the coefficient of sliding friction of the material pairing of the threaded bolt and threaded nut.
In the case of dynamically stressed screws, this may not be sufficient simply because the preload is temporarily removed. So that the preload of the screw connection is always maintained, expansion screws are used or the screw shaft is made as long as possible and tightened with a defined torque that can be calculated for the application.
If sufficient shaft lengths ( clamping length ) are not structurally possible, the necessary increase in friction for movement screws is achieved through small pitch angles and, for connecting screws, additionally through elastic deformation within the thread when screwing in and pretensioning of the screw by tightening.
Typical examples, in which an independent loosening should be prevented, are effective screw locks, cone mountings or shaft-hub-connections by means of a wedge . The construction is very different depending on the application.
Gear, motion thread
With gears, the same effect is achieved through high gear ratios and moments of inertia or low levels of efficiency. A gearbox is self-locking if it can be driven via the input shaft but not via the output shaft. Worm gears in particular can meet this requirement if the pitch angle is smaller than the effective angle of the friction cone .
Furthermore, a distinction is made between gearboxes and threaded spindles
- Dynamic self-locking or self-braking: The drive stops immediately or after a short time, even if a torque is still acting on the output side. In worm gears, the helix angle must be smaller than the angle of the friction cone for sliding friction. Usually this is achieved with worm gears with an efficiency of less than 0.5. Other gears, such as spur gears or planetary gears, are not self-locking even with efficiencies below 0.5. Under no circumstances should the effect replace a brake in safety-relevant areas such as elevators and conveyor systems and with positioning devices, since the self-locking can be canceled even with small bumps or vibrations.
- Static self-locking: The drive only stops in the rest position. When the motor is switched off and there is a load on the output side, the drive does not stop reliably.
The effect that a certain load torque is necessary in order to overcome the drive-side friction or a drive-side cogging torque via the gear ratio in reverse operation shows a similar effect, but is not considered self-locking.
Wedges, cones
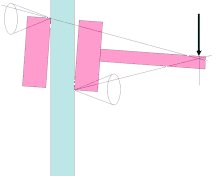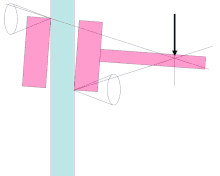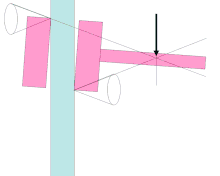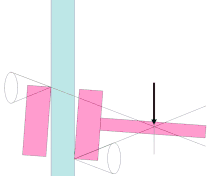
Wedges and cones must have a smaller half-angle than the arctangent of the coefficient of static friction between the wedge and the workpiece to be wedged in order to achieve the necessary clamping force and thus self-locking.
For example, on CNC - machine tools to the tool holder steep taper used because Morse taper act self-locking due to the running cone angle and therefore an automatic tool change can be problematic.
Applications
- In spring-loaded terminals , self-locking means that pulling on the cable cannot disconnect the electrical connection.
- Some freewheel hubs in bicycles achieve the blocking in the blocking direction by self-locking.
- The finger trap works on the principle of self-locking.
- Screw clamps
- Clamps
literature
K. Magnus, HH Müller-Slany: Fundamentals of technical mechanics . 7th edition, Springer 2005 / reprint 2009, ISBN 978-3-8351-0007-7 , page 78
