Symmetrical simple odyssey

Some example paths of the symmetric simple odyssey

The symmetrical simple random walk (up ) is a special stochastic process in probability theory and the simplest example of a random walk . A symmetrical simple random walk is a stochastic process that starts at 0 and then jumps from its current position to either the next larger or the next smaller whole number with each new time step . The probability of jumping up or down is the same, so . ${\displaystyle \mathbb {Z} }$ ${\displaystyle \textstyle {\frac {1}{2}}}$

The symmetrical simple random walk is on the one hand a standard example of the theory of stochastic processes, since it is easy to handle and has some typical phenomena, on the other hand it also models a simple game system. By adapting the simple symmetrical random walk, more complex game processes up to the Cox-Ross-Rubinstein model can be constructed and investigated.

Underlying idea

The symmetrical simple odyssey is based on the idea of ​​playing with a coin. The coin is assumed to be fair, so there is a probability of heads and the same probability of tails. The player tosses the coin repeatedly. The player receives one point if the coin shows “heads” and loses one point if it shows “tails”. At the beginning the player has zero points. The time course of the player's score is then the symmetrical simple random walk. The term "symmetrical" comes from the fact that "heads" and "tails" are equally likely, the player's score is therefore symmetrically distributed around the starting point. ${\displaystyle p={\tfrac {1}{2}}}$

definition

Let an independently and identically distributed sequence of random variables be given , where ${\displaystyle (Y_{n})_{n\in \mathbb {N} }}$

${\displaystyle P(Y_{n}=-1)={\frac {1}{2}}=P(Y_{n}=1)}$

is, so they are distributed by Rademacher . ${\displaystyle Y_{n}}$

Then the time-discrete stochastic process is called with values ​​in defined by ${\displaystyle X=(X_{n})_{n\in \mathbb {N} _{0}}}$ ${\displaystyle \mathbb {Z} }$

${\displaystyle X_{0}=0}$

such as

${\displaystyle X_{n}=\sum _{i=1}^{n}Y_{i}}$

the symmetrical simple random walk. The process can also be equivalent through the start distribution and the transition probabilities ${\displaystyle P(X_{0}=0)=1}$

${\displaystyle P(X_{n+1}=i|X_{n}=j)={\begin{cases}{\tfrac {1}{2}}&{\text{ falls }}i=j+1\\{\tfrac {1}{2}}&{\text{ falls }}i=j-1,\\0&{\text{sonst}}\end{cases}}}$

To be defined.

properties

The symmetric simple random walk is a time-discrete stochastic process because it has the index set . The process only accepts values ​​in , since it starts at zero and only adds up the values ​​−1 and 1. ${\displaystyle T=\mathbb {N} _{0}=\{0,1,2,3,\dots \}}$ ${\displaystyle \mathbb {Z} }$

In addition, it is a stationary increment process that has independent increments .

Distribution properties

The probability that the value takes on is given by ${\displaystyle X_{n}}$ ${\displaystyle k\in \{-n,\dotsc ,n\}}$

${\displaystyle P(X_{n}=k)={\begin{cases}{\binom {n}{(n-k)/2}}2^{-n},&{\text{wenn }}n-k{\text{ gerade ist,}}\\0,&{\text{ sonst.}}\end{cases}}}$

For : is binomially distributed with the parameters and . ${\displaystyle Z_{n}:={\tfrac {1}{2}}(X_{n}+n)}$ ${\displaystyle Z_{n}}$ ${\displaystyle n}$ ${\displaystyle p={\frac {1}{2}}}$

The expected value is

${\displaystyle \operatorname {E} (X_{n})=0}$

and the variance

${\displaystyle \operatorname {Var} (X_{n})=n}$.

As a Markov chain

The symmetric simple random walk is a Markov chain in discrete time with state space . This follows directly from the definition using transition probabilities. More precisely, it is a homogeneous Markov chain (since the transition probabilities do not change) and a Markov chain of the first order , since the transition probabilities only depend on the current state and are not influenced by other previously visited states. ${\displaystyle \mathbb {Z} }$

Irreducibility

The symmetrical simple random walk is an irreducible Markov chain , that is, for any two given integers , the probability is positive that the random walk moves from to . If, for example, were and , the process could move from 10 to 2 in 8 time steps by moving eight times to the left. The probability of this would be and therefore positive. ${\displaystyle i,j}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle i=2}$ ${\displaystyle j=10}$ ${\displaystyle 2^{-8}}$

From the irreducibility it follows directly that the symmetric simple random walk has no absorbing states .

periodicity

Likewise, the symmetric simple random walk is a periodic Markov chain with period two. If one accordingly has the information of the point in time, one can draw conclusions about the duration of the process. From this point of view, the process is not entirely random as it is

• is always on the even numbers at even times . ${\displaystyle n=0,2,4,6,\dots }$ ${\displaystyle \{\dots ,-4,-2,0,2,4,\dots \}}$
• is always on the odd numbers at odd times . ${\displaystyle n=1,3,5,7\dots }$ ${\displaystyle \{\dots ,-3,-1,1,3,\dots \}}$

Return to zero point (recurrence)

The symmetrical simple random walk is recurrent , so it almost certainly returns infinitely to its starting point. A detailed derivation can be found in the article Green function (stochastics) , a statement about higher-dimensional random walks is made by Pólya's theorem .

Modifications

Transition graph of a simple bounded symmetric odyssey in two dimensions. The transition probabilities for states 1, 5 and 6 are shown as examples.

One of the most common variations is to look at the asymmetric simple random walk, the case where a jump to the right is not the same probability as a jump to the left. In particular, the simple random walk is then no longer recurrent.

Other typical modifications are the introduction of dwell probabilities (change in periodicity), temporally variable transition probabilities (inhomogeneity), transition probabilities dependent on the state or the introduction of a memory (Markov chain of higher order).

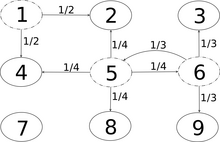
Another classic generalization is the formulation of the simple symmetrical odyssey or one of its modifications in higher dimensions. For example, the symmetrical simple random walk has been well studied. Symmetrical or asymmetrical random walks can also be defined on finite or infinite graphs . ${\displaystyle \mathbb {Z} ^{D}}$

The diagram opposite is an example of a random walk in a two-dimensional world, in which the transition probabilities depend on the state and the graph is finite.

literature

• Achim Klenke: Probability Theory . 3. Edition. Springer-Verlag, Berlin Heidelberg 2013, ISBN 978-3-642-36017-6 , doi : 10.1007 / 978-3-642-36018-3 .
• David Meintrup, Stefan Schäffler: Stochastics . Theory and applications. Springer-Verlag, Berlin Heidelberg New York 2005, ISBN 3-540-21676-6 , doi : 10.1007 / b137972 .

Individual evidence

1. ^ Kohls (2016), Expected Coverage of Random Walk Mobility Algorithm , arxiv.org.