Airy function

This article describes a special function . For the formula that describes the transmission of electromagnetic radiation, see Airy's formula .

The Airy function describes a special function in mathematics. The function and its related function , also called the Airy function, are solutions to the linear differential equation ${\displaystyle \operatorname {Ai} (x)}$ ${\displaystyle \operatorname {Ai} (x)}$ ${\displaystyle \operatorname {Bi} (x)}$

${\displaystyle \ y''-xy=0\ ,}$

also known as the Airy equation. Among other things, it describes the solution of the Schrödinger equation for a linear potential well .

The Airy function is named after the British astronomer George Biddell Airy , who used this function in his work in optics (Airy 1838). The term was introduced by Harold Jeffreys . ${\displaystyle \operatorname {Ai} (x)}$

definition

For real values , the Airy function is defined as a parameter integral: ${\displaystyle x}$

${\displaystyle \mathrm {Ai} (x)={\frac {1}{\pi }}\int \limits _{0}^{\infty }\cos \left({\frac {t^{3}}{3}}+xt\right)\,{\rm {d}}t\ .}$

A second, linearly independent solution of the differential equation is the Airy function of the second kind : ${\displaystyle \mathrm {Bi} }$

${\displaystyle \mathrm {Bi} (x)={\frac {1}{\pi }}\int \limits _{0}^{\infty }\left(\exp \left(-{\frac {t^{3}}{3}}+xt\right)+\sin \left({\frac {t^{3}}{3}}+xt\right)\right)\,{\rm {d}}t\ .}$

properties

Asymptotic behavior

For to be and using the WKB approximation approximate: ${\displaystyle x}$ ${\displaystyle +\infty }$ ${\displaystyle \mathrm {Ai} (x)}$ ${\displaystyle \mathrm {Bi} (x)}$

${\displaystyle {\begin{aligned}\mathrm {Ai} (x)&{}\simeq {\frac {e^{-{\frac {2}{3}}x^{3/2}}}{2{\sqrt {\pi }}\,x^{1/4}}}\\\mathrm {Bi} (x)&{}\simeq {\frac {e^{{\frac {2}{3}}x^{3/2}}}{{\sqrt {\pi }}\,x^{1/4}}}.\end{aligned}}}$

The following relationships apply to against : ${\displaystyle x}$ ${\displaystyle -\infty }$

${\displaystyle {\begin{aligned}\mathrm {Ai} (x)&{}\simeq {\frac {\sin({\frac {2}{3}}(-x)^{3/2}+{\frac {1}{4}}\pi )}{{\sqrt {\pi }}\,(-x)^{1/4}}}\\\mathrm {Bi} (x)&{}\simeq {\frac {\cos({\frac {2}{3}}(-x)^{3/2}+{\frac {1}{4}}\pi )}{{\sqrt {\pi }}\,(-x)^{1/4}}}.\end{aligned}}}$

zeropoint

The Airy functions only have zeros on the negative real axis. The approximate position follows from the asymptotic behavior for to ${\displaystyle x\to -\infty }$

${\displaystyle \operatorname {Ai} (x)=0\quad \Rightarrow \quad x\approx -{\bigl (}\textstyle {\frac {3}{2}}\pi (n-{\frac {1}{4}}){\bigr )}^{2/3},\quad n\in \mathbb {N} }$

${\displaystyle \operatorname {Bi} (x)=0\quad \Rightarrow \quad x\approx -{\bigl (}\textstyle {\frac {3}{2}}\pi (n-{\frac {3}{4}}){\bigr )}^{2/3},\quad n\in \mathbb {N} }$

Special values

The Airy functions and their derivatives have the following values: ${\displaystyle x=0}$

${\displaystyle {\begin{aligned}\mathrm {Ai} (0)&{}={\frac {1}{{\sqrt[{3}]{9}}\cdot \Gamma ({\frac {2}{3}})}},&\quad \mathrm {Ai} '(0)&{}=-{\frac {1}{{\sqrt[{3}]{3}}\cdot \Gamma ({\frac {1}{3}})}},\\\mathrm {Bi} (0)&{}={\frac {1}{{\sqrt[{6}]{3}}\cdot \Gamma ({\frac {2}{3}})}},&\quad \mathrm {Bi} '(0)&{}={\frac {\sqrt[{6}]{3}}{\Gamma ({\frac {1}{3}})}}.\end{aligned}}}$

This is the gamma function . It follows that the Wronsky determinant of and is equal . ${\displaystyle \Gamma (\cdot )}$ ${\displaystyle \mathrm {Ai} (x)}$ ${\displaystyle \mathrm {Bi} (x)}$ ${\displaystyle {\tfrac {1}{\pi }}}$

Fourier transform

Its Fourier transform follows directly from the definition of the Airy function (see above) . ${\displaystyle \operatorname {Ai} (x)}$

${\displaystyle {\mathcal {F}}(\operatorname {Ai} )(k):=\int _{-\infty }^{\infty }\operatorname {Ai} (x)\ \mathrm {e} ^{-2\pi \mathrm {i} kx}\,dx=\mathrm {e} ^{{\frac {\mathrm {i} }{3}}(2\pi k)^{3}}\,.}$

Note the symmetrical variant of the Fourier transform used here.

Further representations

• Using the hypergeometric function ${\displaystyle {}_{0}F_{1}}$

${\displaystyle \mathrm {Ai} (z)={\frac {1}{3^{2/3}\cdot \Gamma ({\tfrac {2}{3}})}}\cdot \,{}_{0}F_{1}\left(0;{\tfrac {2}{3}};{\tfrac {1}{9}}z^{3}\right)-{\frac {z}{3^{1/3}\cdot \Gamma ({\tfrac {1}{3}})}}\cdot \,{}_{0}F_{1}\left(0;{\tfrac {4}{3}};{\tfrac {1}{9}}z^{3}\right)}$

${\displaystyle \mathrm {Bi} (z)={\frac {1}{3^{1/6}\cdot \Gamma ({\tfrac {2}{3}})}}\cdot \,{}_{0}F_{1}\left(0;{\tfrac {2}{3}};{\tfrac {1}{9}}z^{3}\right)+{\frac {3^{1/6}\cdot z}{\Gamma ({\tfrac {1}{3}})}}\cdot \,{}_{0}F_{1}\left(0;{\tfrac {4}{3}};{\tfrac {1}{9}}z^{3}\right)}$

• For they can also be represented with the modified Bessel function of the first kind as follows: ${\displaystyle x>0}$ ${\displaystyle I}$

${\displaystyle \mathrm {Ai} (x)={\frac {1}{3}}{\sqrt {x}}\left[I_{-1/3}\left({\frac {2}{3}}x^{3/2}\right)-I_{1/3}\left({\frac {2}{3}}x^{3/2}\right)\right]}$

${\displaystyle \mathrm {Bi} (x)={\sqrt {\frac {x}{3}}}\left[I_{-1/3}\left({\frac {2}{3}}x^{3/2}\right)+I_{1/3}\left({\frac {2}{3}}x^{3/2}\right)\right]}$

• Another infinite integral representation for is ${\displaystyle \mathrm {Ai} }$

${\displaystyle \mathrm {Ai} (z)={\frac {1}{2\pi }}\int \limits _{-\infty }^{\infty }\exp \left(\mathrm {i} \cdot \left(zt+{\frac {t^{3}}{3}}\right)\right)\mathrm {d} t}$

• There are the series representations

${\displaystyle \mathrm {Ai} (z)={\frac {1}{3^{2/3}\pi }}\sum _{n=0}^{\infty }{\frac {\Gamma \left({\frac {1}{3}}(n+1)\right)}{n!}}\left(3^{1/3}z\right)^{n}\sin \left({\frac {2(n+1)\pi }{3}}\right)}$

${\displaystyle \mathrm {Bi} (z)={\frac {1}{3^{1/6}\pi }}\sum _{n=0}^{\infty }{\frac {\Gamma \left({\frac {1}{3}}(n+1)\right)}{n!}}\left(3^{1/3}z\right)^{n}\left|\sin \left({\frac {2(n+1)\pi }{3}}\right)\right|}$

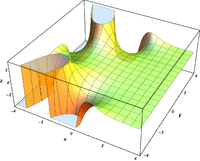
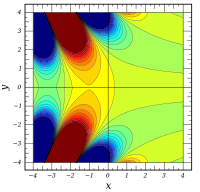
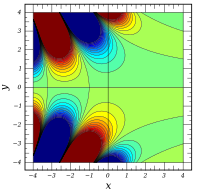
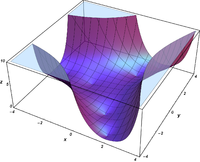
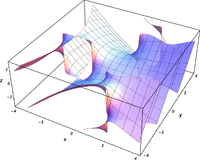
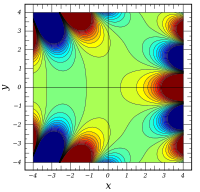
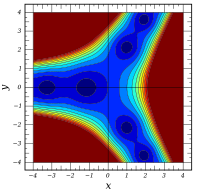
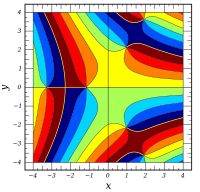
Complex arguments

${\displaystyle \mathrm {Ai} (x)}$and are whole functions . So they can be continued analytically on the entire complex level. ${\displaystyle \mathrm {Bi} (x)}$

${\displaystyle \Re \left[\mathrm {Ai} (x+iy)\right]}$	${\displaystyle \Im \left[\mathrm {Ai} (x+iy)\right]}$	${\displaystyle |\mathrm {Ai} (x+iy)|\,}$	${\displaystyle \mathrm {arg} \left[\mathrm {Ai} (x+iy)\right]\,}$

${\displaystyle \Re \left[\mathrm {Bi} (x+iy)\right]}$	${\displaystyle \Im \left[\mathrm {Bi} (x+iy)\right]}$	${\displaystyle |\mathrm {Bi} (x+iy)|\,}$	${\displaystyle \mathrm {arg} \left[\mathrm {Bi} (x+iy)\right]\,}$

Related functions

Airy zeta function

Analogous to the other zeta functions, the Airy zeta function can be defined for the Airy function as

${\displaystyle Z(n)=\sum _{r}{\frac {1}{r^{n}}},}$

where the sum goes over the real (negative) zeros of . ${\displaystyle \mathrm {Ai} }$

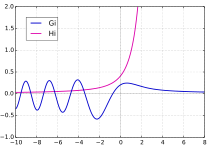
Scorer functions

Function graphs of and . ${\displaystyle \mathrm {Gi} (x)}$ ${\displaystyle \mathrm {Hi} (x)}$

Sometimes the two other functions and are added to the Airy functions. The integral definitions are ${\displaystyle \mathrm {Gi} (x)}$ ${\displaystyle \mathrm {Hi} (x)}$

${\displaystyle \mathrm {Gi} (x)={\frac {1}{\pi }}\int \limits _{0}^{\infty }\sin \left({\frac {t^{3}}{3}}+xt\right)\,\mathrm {d} t}$

${\displaystyle \mathrm {Hi} (x)={\frac {1}{\pi }}\int \limits _{0}^{\infty }\exp \left(-{\frac {t^{3}}{3}}+xt\right)\,\mathrm {d} t}$

They can also be represented by the functions and . ${\displaystyle \mathrm {Ai} }$ ${\displaystyle \mathrm {Bi} }$

literature

• Milton Abramowitz , Irene A. Stegun : Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables . (see §10.4) . National Bureau of Standards , 1954.
• George Biddell Airy: On the intensity of light in the neighborhood of a caustic . In: Transactions of the Cambridge Philosophical Society. Volume 6, 1838, pp. 379-402.
• Frank Olver: Asymptotics and Special Functions. Chapter 11. Academic Press, New York 1974.

Web links

Commons : Airy function  - collection of pictures, videos and audio files

• Eric W. Weisstein : Airy Functions . In: MathWorld (English).
• Bessel-type functions . Tungsten functional side.
• Chapter 9: Airy and related functions . In: Digital Library of Mathematical Functions.

Individual evidence

1. ↑ Eric W. Weisstein : Airy Function Zeros . In: MathWorld (English).
2. ↑ C. Banderier, P. Flajolet, G. Schaeffer, M. Soria: Planar Maps and Airy Phenomena. In Automata, Languages ​​and Programming. Proceedings of the 27th International Colloquium (ICALP 2000) held at the University of Geneva , Geneva, 9. – 15. July 2000 (Ed. U. Montanari, JDP Rolim, E. Welzl). Berlin: Springer, pp. 388-402, 2000
3. ↑ Eric W. Weisstein : Airy Zeta Function . In: MathWorld (English).
4. ↑ Milton Abramowitz and Irene A. Stegun: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables , 1954, page 447