Asymmetric cryptosystem
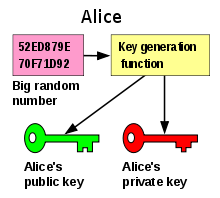
Asymmetric cryptosystem is a generic term for public-key encryption methods , public-key authentication and digital signatures . The “asymmetric cryptosystem” or “public key cryptosystem” is a cryptographic procedure in which, in contrast to a symmetric cryptosystem, the communicating parties do not need to know a shared secret key . Each user generates his own key pair, which consists of a secret part ( private key ) and a non-secret part ( public key ). The public key enables anyone to encrypt data for the owner of the private key , to check their digital signatures or to authenticate them. The private key enables its owner to decrypt data encrypted with the public key , to generate digital signatures or to authenticate himself .
A public key encryption method is a method of converting plain text into ciphertext with a public key , from which the plain text can be retrieved with a private key .
principle
The private key must be kept secret and it must be practically impossible to calculate it from the public key. The public key must be accessible to anyone who wants to send an encrypted message to the owner of the private key. It must be ensured that the public key is actually assigned to the recipient.
The theoretical basis for asymmetric cryptosystems are trapdoor functions , ie functions that are easy to calculate but are practically impossible to invert without a secret (the “trapdoor”). The public key is then a description of the function, the private key is the trapdoor. A prerequisite is of course that the private key cannot be calculated from the public one. In order for the cryptosystem to be used, the public key must be known to the communication partner.
The decisive advantage of asymmetric methods is that they reduce the key distribution problem. In the case of symmetrical procedures, a key must have a secure, i. E. H. Tap-proof and tamper-proof channels can be exchanged. Since the public key is not secret, the channel does not need to be secure against eavesdropping in asymmetrical procedures; The only important thing is that the public key can be assigned unequivocally to the owner of the associated private key. For this purpose, for example, a trustworthy certification authority can issue a digital certificate that assigns the public key to the private key (owner). As an alternative to this, a trust network ( web of trust ) can also be set up without a central point by mutual certification of keys .
safety
For the security of asymmetrical processes, it is necessary that the one-way functions on which the various processes are based are practically irreversible, since otherwise the private key could be calculated from the public key. The security of all asymmetric cryptosystems is currently based on unproven assumptions, in particular on the assumption that P is not equal to NP . The non-reversibility of the trapdoor functions used has not been proven. Typically, however, these assumptions are strongly presumed to be correct. The information-theoretical security that can be achieved with the symmetrical one-time pad can not be achieved with an asymmetrical procedure because a suitably powerful attacker can always solve the underlying mathematical problem.
Practical aspects
Asymmetric cryptosystems have the advantage that they keep the secret as small as possible, since each user only has to keep his own private key secret. In contrast to this, with a symmetrical cryptosystem, every user has to keep all keys secret, which means that the workload increases with the number of users.
Compared to symmetric algorithms, the asymmetric algorithms work very slowly. In practice, this problem is circumvented in different ways. Hybrid methods are used for encryption , in which only a symmetric key is encrypted with the asymmetric method and the actual message is encrypted with this symmetric key. With digital signatures, instead of a message, only the hash value is signed.
history
Until the 1970s, there were only symmetrical cryptosystems in which the sender and recipient had to have the same key. This raises the problem of key exchange and key management. Ralph Merkle took the first step in the development of asymmetrical processes in 1974 with the Merkles Puzzle named after him , which was not published until 1978. The first public key encryption method was the Merkle-Hellman cryptosystem developed by Ralph Merkle and Martin Hellman . The MH procedure was broken in 1983 by Adi Shamir . In the summer of 1975 Whitfield Diffie and Martin Hellman published an idea for asymmetric encryption, but without knowing a precise method. Under the influence of this work, Diffie and Hellman developed the Diffie-Hellman key exchange in 1976 .
The first asymmetric encryption method was developed in 1977 by Ronald L. Rivest , Adi Shamir and Leonard M. Adleman at MIT and named after them the RSA method . According to today's terminology, this process is a trap door permutation that can be used both for the construction of encryption processes and signature processes.
Independent of the developments in scientific cryptology , in the early 1970s three employees of the British Government Communications Headquarters , James H. Ellis , Clifford Cocks and Malcolm Williamson , set up both the later Diffie-Hellman key exchange and one similar to the RSA cryptosystem asymmetrical procedure was developed, which, however, was not published for reasons of confidentiality and a patent was not applied for.
| year | Cryptosystem |
|---|---|
| 1977 | RSA |
| 1978 | Merkle-Hellman |
| 1978 | McEliece |
| 1979 | Rabin |
| 1984 | Choir Rivest |
| 1985 | Elgamal |
Formal definition
Formally, a public key encryption method consists of three algorithms :
- The key generation algorithm generates a key pair for a given security parameter, which consists of a public key and the associated secret key.
- The encryption algorithm generates a ciphertext from a plain text using the public key. There can be several ciphertexts for one plaintext. In this case the algorithm is probabilistic .
- The decryption algorithm calculates the appropriate plain text for a ciphertext using the secret key.
It is now required that every message that was encrypted with a public key can be retrieved from the cipher with the associated secret key .
application
These methods are used nowadays e.g. B. used in e-mail traffic ( OpenPGP , S / MIME ) as well as in cryptographic protocols such as SSH or SSL / TLS . SSL / TLS is used to a greater extent, for example as the https protocol for secure communication between a web browser and a server.
The public key is used for encryption on the text to be encrypted. The encrypted text is then decrypted again by the key holder using the private key.
Digital signatures are sometimes a. used to conduct business securely on the Internet. Here they enable the identity of the contracting party to be checked and the authenticity of the data exchanged ( electronic signature ). This usually requires a public key infrastructure that confirms the validity of the keys used with certificates .
To create a signature, a hash value is created from the message to be sent and signed with the private key. The message and signature are then sent to the recipient, whereby the actual signature does not need to be encrypted, as this is a signature (creating integrity and authenticity) and not encryption (creating confidentiality).
To verify the signature, the received signature of the hash value is checked with the public key. If the verification is successful, it can be assumed that the message originates from the owner of the private key and that the message was not manipulated during transmission.
literature
Used literature
- Steve Burnett Stephen Paine: RSA Security's Cryptography Official Guide. 1st edition. mitp-Verlag, Bonn 2001, ISBN 3-8266-0780-5
- Simon Singh: Codes. dtv, Munich 2002, ISBN 3-423-62167-2 (excerpt from Secret Messages )
- Simon Singh: Secret Messages . 4th edition. dtv, Munich 2001, ISBN 3-423-33071-6
- Reinhard Wobst: Adventure cryptology. 3. Edition. Addison-Wesley, Munich 2003, ISBN 3-8273-1815-7
further reading
- Albrecht Beutelspacher , Jörg Schwenk, Klaus-Dieter Wolfenstetter: Modern methods of cryptography. From RSA to zero knowledge. 4th edition. Vieweg-Verlag, June 2001, ISBN 3-528-36590-0
- Wolfgang Ertel : Applied cryptography . Hanser Fachbuchverlag, Munich / Vienna 2003, ISBN 3-446-22304-5
- Bruce Schneier : Applied Cryptography . Second edition. John Wiley & Sons, 1996, ISBN 0-471-11709-9
- Jonathan Katz and Yehuda Lindell: Introduction to Modern Cryptography . CRC Press, 2007, ISBN 1-58488-551-3 .
- Alfred J. Menezes; PC van Oorschot; Scott A. Vanstone: Handbook of Applied Cryptography . 1997, ISBN 0-8493-8523-7 ( uwaterloo.ca ).
Web links
- CrypTool - extensive learning program on classical and modern procedures plus reading material on cryptology - see. a. CrypTool
- Asymmetric encryption clearly illustrated. Also as a Powerpoint presentation
- Klaus Pommerening: Asymmetrical encryption . (PDF; 619 kB) Department of Mathematics at Johannes Gutenberg University
Individual evidence
- ↑ Ralph Merkle and Martin Hellman: Hiding information and signatures in trapdoor knapsacks . In: Information Theory, IEEE Transactions on . tape 24 , no. 5 , 1978, p. 525-530 ( ieee.org ).
- ^ Adi Shamir: A Polynomial Time Algorithm for Breaking the Basic Merkle-Hellman Cryptosystem . In: Proceedings of CRYPTO . 1982, p. 279-288 .
- ^ W. Diffie, ME Hellman: New Directions in Cryptography . In: IEEE Transactions on Information Theory . tape 22 , no. 6 , 1976, p. 644–654 ( cs.jhu.edu (PDF; 267 kB) other version).
- ↑ Ronald L. Rivest, Adi Shamir, and Leonard Adleman: A Method for Obtaining Digital Signatures and Public-Key Cryptosystems . ( with.edu [PDF]).