Diffie-Hellman key exchange

The Diffie-Hellman key exchange or Diffie-Hellman-Merkle key exchange or key agreement (also short DHM key exchange or DHM protocol ) is a protocol for key agreement . It enables two communication partners to agree on a shared secret key in the form of a number via a public, eavesdropping line , which only they know and a potential eavesdropper cannot calculate. The key thus agreed can then be used for a symmetrical cryptosystem (for example Data Encryption Standard or Advanced Encryption Standard ). Different variants of the Diffie-Hellman-Merkle process are used today for key distribution in the communication and security protocols of the Internet , for example in the areas of electronic commerce . This principle therefore has an important practical meaning.
The method was developed by Whitfield Diffie and Martin Hellman and published in 1976 under the name ax1x2 . It is the first of the so-called asymmetric cryptographic processes (also known as public key cryptographic processes ) to be published. Ralph Merkle carried out important preliminary work with the Merkles puzzle named after him . As only became known in 1997, employees of the British Government Communications Headquarters (GCHQ) were the first to develop asymmetric cryptosystems in the early 1970s . However, the GCHQ has never applied for a patent because of the secrecy and because of the questionable benefit for the British from the perspective of the early 1970s.
The DHM key exchange is one of the crypto systems based on the discrete logarithm (short: DL procedure). These are based on the fact that the discrete exponential function is a one-way function in certain cyclic groups . In the prime residue class group, the discrete exponential function , prime , can also be calculated efficiently for large exponents , but its inverse , the discrete logarithm, cannot. To date, there is no "fast" algorithm for calculating the exponent , given the basis , module and desired result.
With the method, the researchers also coined a new security concept in cryptography, which is based on the fact that there is no efficient algorithm for cryptanalysis : A communication protocol is secure if its cryptanalysis means so much time and work that it is not carried out in practice can be. The problem of calculating the secret key from the two messages from the communication partners is known as the Diffie-Hellman problem .
However, the DHM key exchange is no longer secure if an attacker switches between the two communication partners and can change messages. This gap is closed by protocols such as the station-to-station protocol (STS) by using digital signatures and message authentication codes .
The implementation using elliptic curves is known as the Elliptic Curve Diffie-Hellman (ECDH). The operations used in the original method (multiplication and exponentiation) on the finite body are replaced by point addition and scalar multiplication on elliptic curves . The -fold addition of a point to itself (i.e. the multiplication with the scalar ) is denoted by and corresponds to an exponentiation in the original method. The principle was proposed by Victor S. Miller and Neal Koblitz independently of one another in the mid-1980s .
History and meaning
Public cryptology
The Diffie-Hellman-Merkle key exchange is the first of the so-called asymmetric cryptographic methods (also known as public key cryptographic methods) to be published. It solves the key exchange problem by making it possible to negotiate secret keys via non-secret, i.e. public, channels.
Ralph Merkle took the first step in the development of asymmetrical methods in 1974 with the Merkles Puzzle named after him , which was not published until 1978. Influenced by this work, Whitfield Diffie and Martin Hellman developed the Diffie-Hellman key exchange in 1976. They published the research paper under the title "New Directions in Cryptography". The process gave a huge boost to cryptography , a science that was not publicly practiced for very long at the time. The researchers originally called the process ax1x2. In 2002, Martin Hellman suggested that the process should be called Diffie-Hellman-Merkle key exchange “if names are connected to it”, in recognition of Ralph Merkle's contribution to the development of asymmetric processes.
The significance of this development is also compared with the Copernican turn : "The development of asymmetric encryption has a similar meaning for cryptography as the Copernican turn for astronomy and represents, in addition to the digitization of information and the Internet as a communication platform, a foundation of the third millennium . "
With the process, Whitfield Diffie and Martin Hellman also coined a new security concept in cryptography, which is based on the fact that there is no efficient algorithm for cryptanalysis : A communication protocol is secure if its cryptanalysis means so much time and work that it does in practice cannot be executed. The security of the Diffie-Hellman key exchange is based Merkle crucial that the discrete exponential function in certain cyclic groups a one-way function (English one-way function ), so particularly in the reduced residue class group . This means that the exponentiation can be calculated efficiently in this , but no efficient algorithm is known for its inverse, the discrete logarithm , to this day.
The Diffie-Hellman-Merkle method is now just one of many methods that use the discrete exponential function (with the discrete logarithm as the inverse) as a one-way function. In this context, one speaks of cryptographic systems based on the discrete logarithm or simply of DL procedures. For example, it is closely related to the Elgamal encryption method , which was developed in 1985 by the cryptologist Taher Elgamal . In principle, this is nothing more than a DHM key exchange with subsequent sending of a message that is encrypted with the agreed key.
In their fundamental “New Directions” work, the researchers also introduced the concept of a digital signature : a sender uses a secret signature key (the private key) to calculate a value for a digital message (ie for any data), known as the digital signature becomes. This value enables anyone to use the public key to verify the non-repudiable authorship and integrity of the message. As a further development of the DHM key exchange, a diverse family of digital signatures based on the discrete logarithm was created. The best known are the Elgamal signature process and the Digital Signature Algorithm .
In addition to the one-way function Whitfield Diffie and Martin Hellman developed the concept of trapdoor (English trapdoor ). This is a "hidden abbreviation" with additional information that makes the otherwise difficult reversal easy. On the basis of trapdoor functions, asymmetrical procedures can be developed in which the transmission of a secret key is no longer necessary. In doing so, they also performed important preparatory work for the development of the RSA cryptosystem . Ronald L. Rivest , Adi Shamir and Leonard Adleman were actually trying to prove that such trapdoor functions cannot exist. However, in the attempted proof, they actually came across such a one-way function with a trap door. This led to the development of the most famous public key algorithm in 1977, the so-called RSA cryptosystem after the initials of its inventors.
Different variants of the DHM process are used today for key distribution in the communication and security protocols of the Internet, such as B. IPsec ( Internet Protocol Security ), IPv6 ( Internet Protocol Version 6 ) and TLS ( Transport Layer Security ). These serve to secure the transmission of data packets of the IP protocol layer or of data of the application level, for example in the areas of electronic commerce . This principle of key distribution therefore has an important practical meaning. The key that is automatically calculated here is then used as the key for a fast symmetrical procedure such as Data Encryption Standard (DES) or Advanced Encryption Standard (AES).
The concept of public key cryptography and some specific methods were protected until 1997 by US Patents 4,200,770 (Hellman, Diffie, Merkle, 1980) and 4,218,582 (Hellman, Merkle, 1980), which belong to Stanford University . For the development of public key cryptography and the digital signature, Whitfield Diffie and Martin Hellman received the Turing Award in 2015 , which is considered the highest distinction in computer science, comparable to the Nobel Prize or the Fields Medal .
Secret cryptology
As only became known in 1997, the British Government Communications Headquarters (GCHQ) had already given the order in the 1960s to find a different way to avoid the high costs of the key distribution that was common at the time. James H. Ellis formulated the concept of "non-secret encryption". From this, Clifford Cocks developed a process that he described in an internal document as early as 1973 and that is very similar to the RSA process . From today's perspective, it must therefore be stated that Clifford Cocks was actually the first to develop an asymmetrical crypto process. This achievement is not universally recognized because his work was by definition classified and therefore not published at the time. It was not until 1997 that the internal document was published on the Communications Electronics Security Group website.
In this context, it was also announced that Malcolm Williamson , another GCHQ employee, discovered the Diffie-Hellman key exchange procedure as early as 1975. It is interesting that the two methods - RSA and DHM - were discovered in public and secret cryptology in reverse order.
Key exchange problem
Encryption methods in which two participants use the same secret key are called symmetric methods . Be Alice and Bob transmitters and receivers of messages that may be intercepted over a canal and was Eve (of English. Eavesdropper to German eavesdroppers / Lauscherin) an eavesdropper who tries to read along messages. With a good encryption method, it is impossible for Eve to decrypt a message without knowing the key, even if she knows the encryption method. Kerckhoffs' principle states that the security of a procedure must be based solely on the secrecy of a key (and not on the secrecy of the encryption algorithm ). A message that is encrypted is called plain text , the encrypted text is called ciphertext .
An important prerequisite for secure symmetrical communication is that the key between Alice and Bob has already been exchanged via a secure route, for example by a trustworthy courier or during a direct meeting. The following problem arises with the key exchange problem: Alice wants to communicate with Bob, who is, for example, overseas, using a symmetrical encryption method. The two are connected via an insecure line and have not exchanged a key. How do Alice and Bob agree on a shared secret key over an insecure channel?
A manual key exchange has the disadvantage that it becomes quite confusing when a larger group of users wants to communicate with one another in encrypted form. With communication partners, keys are required if everyone wants to communicate with everyone. With 50 communication partners, a total of 1,225 keys would be required.
The Diffie-Hellman method provides an elegant solution to these problems: It allows Alice and Bob to negotiate a secret key over the public, unsecured line without Eve knowing the key.
Mathematical basics
Note: The following considerations convey the mathematical fundamentals of asymmetrical cryptographic processes based on the discrete logarithm. The individual sections are limited in particular to the essential aspects that are necessary for the design and security analysis of the Diffie-Hellman-Merkle key exchange. In order to maintain a certain clarity, some aspects are presented in a simplified manner. For more in-depth considerations and proofs, please refer to the literature on the mathematical fundamentals in the literature section.
One-way functions
A one-way function is a mathematical function that is “easy” to calculate in terms of complexity theory , but “difficult” to reverse . A mathematical one-way function must have the following properties:
- The calculation of the function value is "easy"; H. there is an algorithm that can calculate it in polynomial time.
- The calculation of the inverse function for a given function value , i.e. H. one , so , is "difficult", i. H. there is no "fast" algorithm for this problem. “Fast” here means a probabilistic algorithm that runs in polynomial time.
A classic paper phone book from a larger city offers a clear comparison: The function to be performed is to assign the corresponding telephone number to a name. Since the names are arranged alphabetically, this can be done fairly quickly. But their inversion, i.e. the assignment of a name to a given telephone number, is obviously much more difficult.
One can show that one-way functions exist if and only if P ≠ NP, the famous conjecture from complexity theory, holds (see P-NP problem ). Although the one-way functions play an important role in cryptography, it is still not known whether they even exist in a strictly mathematical sense.
The security of the DHM key exchange is based on the fact that the discrete logarithm is assumed to be a one-way function in certain cyclic groups . There is no trap door; H. additional information with which the inverse function could easily be calculated. In contrast, the RSA cryptosystem , for example, uses a one-way function with a trap door with factorization .
Discrete exponential function and discrete logarithm
The discrete exponential function
returns the remainder when dividing by m. The inverse of the discrete exponential function is called the discrete logarithm .
The discrete exponential function can also be calculated efficiently for large exponents . Even for numbers over a hundred bits long, one second on a PC is sufficient if implemented skillfully . Euler's theorem and the square & multiply method can be used for efficient calculation .
For the inversion, i.e. the calculation of the exponent , given the basis , module and desired result, no fast algorithm is known to date: Even with the greatest hardware expenditure and the best known algorithms , calculation times of several thousand bits can quickly be achieved over the lifetime of our universe.
According to current knowledge, the discrete exponential function is therefore a one-way function. However, since there is no mathematical proof of their existence, it would theoretically be possible that one day a quick method for computing the discrete logarithm would be found. However, since this has been tried unsuccessfully for a long time, one can assume that this case will never occur.
Example:
The discrete exponential function assigns the result of . The remainder for the module is calculated in the calculation . This creates a finite number range . The figure is clear for the values . The discrete logarithm is the inverse function, i.e. the assignment from to .
Group theory
A group is a pair consisting of an amount and an associative link on which a neutral element has and for each element of an inverse element has. If the commutative law also applies to a group , it is called an Abelian group . A subgroup of a group is a subset of which is itself a group in terms of the linkage .
For example, the set of whole numbers with addition as a link forms the (Abelian) group . The neutral element of addition is the ( zero ) and the additive inverse of a number is its opposite number . The whole numbers are in turn a subgroup of the rational numbers with regard to addition . In contrast, the rational (and whole) numbers do not form a group together with the multiplication , because the number has no inverse element with respect to the multiplication. However, if one of away, you get the (Abelian) group .
A cyclic group is a group whose elements can be represented as the power of one of its elements. Using multiplicative notation, the elements of a cyclic group are
- ,
where means and denotes the neutral element of the group. The element is called the producer or the primitive root of the group. A cyclic group therefore only consists of the powers of the generator :
In a group , the thickness is also referred to as the order of the group . So for a finite group the order is simply the number of group elements. The set of Lagrange stating that the order of each subgroup of a finite group shares their thickness.
Prime residual class group and primitive root
The prime remainder class group is the group of the prime remainder classes with respect to a module . It is noted as or . The prime residue classes are precisely the multiplicatively invertible residue classes and are therefore finite Abelian groups with regard to multiplication . For example, the set does not form a group with the multiplication modulo as a link, even if it is excluded. There are other numbers that do not have an inverse element, namely , and . These are exactly the numbers that have a real factor in common with. The remaining elements eventually form the multiplicative group
In cryptography, those numbers are of particular interest for which all numbers between and have an inverse element modulo . This is exactly the case if is a prime number (which is why one writes instead of ). The numbers between and together with the modulo multiplication form the group . Another statement that can be proved: Taking any element of and considered the amount , then you get a sub-group ( as a generator of the subgroup). Each subgroup of has at least one generator, and thus also itself. The group is therefore cyclic. For example, there is a cyclic group with the as a generator, because every number from to can be represented as a power of :
For a generator, on the other hand, you only get the subgroup with the elements :
It can now easily be seen that the equation is always solvable if there is a generator of , in which case an element of is (except ). The discrete logarithm always exists in when the base is a generator of . If you represent the numbers in a circle (cycle) of powers, they seem to be distributed arbitrarily. This gives at least an idea of why the discrete logarithm is so laborious to determine.
A generating element of is also called a primitive root to the module . So the number is a primitive root modulo , but the number is not. All elements of the prime residue class group can be represented modulo as powers of . In the sequence of the powers of modulo , however, the remainders are repeated (see above).
For a prime number there is exactly primitive roots , which for the Euler phi function is that for each natural number the number of its prime indicates natural numbers.
For is and , it follows that it primitive roots modulo are (namely , , and ).
It has been proven that exactly different primitive roots exist modulo for every prime number , but no algorithm is known that can also efficiently compute any primitive root . If given and the factorization of is unknown, one can at least test whether a random number is a primitive root modulo . The following must apply:
- and for .
Such a check cannot be carried out for cryptographically relevant prime numbers due to the size of .
If, on the other hand, the prime factorization of is known, then a primitive root is modulo if and only if holds
- for all prime factors .
The “primitive root test” becomes particularly easy when it is valid with a prime number . Then you just need to test whether
- and
is. If this is the case, then a primitive root is modulo .
Example:
Be . Then with is prime. To test whether any number is a primitive root modulo is must and will be checked. For example, and . So a primitive root is modulo . The others are 7, 10, 11, 14, 15, 17, 19, 20 and 21. With you can see that (all 10) primitive roots are found modulo .
functionality
Illustration of the basic idea using mixed colors
First of all, the basic idea of the Diffie-Hellman-Merkle key exchange should be clearly illustrated by means of “mixing colors”, as illustrated in the illustration on the left. In reality, the colors would be numbers, and mixing colors would be the discrete exponential function.
Mixing colors is seen here as a one-way function: it is "easy" to mix two or more different colors. However, the reverse, the breaking down of a color mixture into its original color components, is very time-consuming, i.e. it cannot be carried out efficiently.
Alice and Bob first publicly agree on a common color (in the example yellow). In addition, each of the two communication partners chooses a secret color (Alice Orange and Bob Turquoise). Bob and Alice now mix the common color with their secret color. In the example, the result is beige for Alice and gray-blue for Bob. Alice and Bob exchange these color mixes over the audible line. It is not possible for a potential eavesdropper Eve to infer the secret colors of Alice and Bob from the public information (yellow, beige, gray-blue).
In a final step, Alice and Bob mix the color mixture of their counterpart with their own secret color. This in turn results in a new color (ocher brown in the example) that is the same for both communication partners (yellow + orange + turquoise = yellow + turquoise + orange = ocher brown). So Alice and Bob have a common secret color. It's impossible for Eve to find out because she doesn't know Alice and Bob's secret color ingredients.
Mathematical functioning
The two communication partners Alice and Bob want to communicate in encrypted form using an insecure medium, such as a cable or radio connection. A symmetrical cryptosystem is to be used for this purpose, but for which both initially need a shared secret key. The DHM communication protocol ensures that you can calculate a secret key without third parties (EVE) being able to find out. You can then use the key calculated in this way in the future to communicate in encrypted form with a symmetrical cryptosystem.
- Alice and Bob first publicly agree on a large prime number and a natural number that is less than . Publicly agreeing on them means that everyone can know these two numbers (including potential eavesdroppers like Eve). Ideally, it is a generator of the cyclical group , but the method also works if another value assumes less . In practice, it is usually the case that and are given and used by many users.
- Alice and Bob each generate a secret random number (private key) or from the set . and are not transmitted, so they remain unknown to potential eavesdroppers, but also to the respective communication partner. Only Alice knows the number and only Bob knows the number .
- Alice uses her secret number to calculate the public key and sends it to Bob. Bob uses his secret number to calculate the public key and sends it to Alice.
- Alice receives from Bob and uses her private key to calculate the number . Bob calculated with the obtained and its private key is also the number . The two calculated the same number . This is the shared key we are looking for .
Only Alice and Bob know . Eve can not calculate from the intercepted communication . To do this, it would have to solve the discrete logarithm, which according to current knowledge is not efficiently possible if the numbers are large enough. Alice and Bob can therefore safely use symmetrical encryption.
The following two residual class equations show that both communication partners calculate the same value for :
- .
- .
Since the multiplication is commutative , the following also applies
and thus
- .
So Alice and Bob get exactly the same number after their respective calculations, namely the secret key .
Example:
The following example serves as an illustration and therefore uses very small numbers. In actual application, however, numbers with at least several hundred digits are used.
- Alice and Bob agree on the two public keys and ( is a generator of the group , see section "Group theory").
- Alice chooses the random number as the secret key and Bob .
- Now Alice calculates and sends to Bob. Bob calculates and sends to Alice.
- Alice calculates . Bob calculates .
- Both get the same result .
The eavesdropper Eve can overhear the numbers 13, 2, 6 and 9, but the actual shared secret of Alice and Bob remains hidden from her. can be used as a key for subsequent communication.
With the help of the intercepted messages, Eve can at least set up the following equations:
From this, she can determine the two secret numbers and , for example, by trial and error . She can now take the agreed key from Alice and Bob with
calculate.
However, if the prime number is chosen large enough and a generator of the group is used, it is too time-consuming for Eve to try out all the numbers between and that come into question as a result of the modular power .
safety
Diffie-Hellman problem
Computational Diffie Hellman Problem (CDH)
Assuming that the eavesdropper Eve learns to the uncertain line numbers , , and , but not the discrete logarithms of and of the base . With the knowledge of and it would be an easy task for them to determine the key . The numbers and however out is very difficult when the numbers , and are very large, for example numbers with several hundred places in the decimal system . The computational Diffie-Hellman problem results from this problem:
- If an element of a group and the values and are given, then what value has with unknown?
Since this problem can only be solved with enormous computing effort in certain groups, an attacker cannot calculate the key generated from the two messages transmitted during the Diffie-Hellman-Merkle key exchange.
The Diffie-Hellman problem is closely related to the discrete logarithm problem . Computing discrete logarithms is the only known way to break the DEM method. As long as this cannot be solved in a reasonable time, it is impossible for an attacker to determine the secret key. However, it has not been proven that this is actually the only method of whether someone who could solve the Diffie-Hellman problem could also compute discrete logarithms efficiently. Ueli Maurer has shown that both problems are equivalent, at least under certain conditions.
Decisional Diffie Hellman Problem (DDH)
If it is to be impossible for an attacker to obtain any information about the transported key from the publicly available information, the Decisional Diffie Hellman Problem (DDH) must be invulnerable. This problem can be described as follows:
- An attacker receives three numbers: , and . Either , and randomly and evenly distributed in were chosen or set. The second case is called Diffie-Hellman triple. The attacker has to decide whether there is such a triple or not. Can he not that, it's impossible for him out and conclusions to draw to.
The problem, therefore, is a given , and to decide whether is.
Anyone who can solve the Computational Diffie-Hellman Problem is obviously also able to solve the Decisional Diffie-Hellman Problem. In the opposite case it is not clear.
When choosing as the primitive root , the Decisional Diffie-Hellman problem can be attacked. This is based on the following theorem:
- Let be a prime number, be a primitive root modulo and be . Then a quadratic remainder is modulo if and only if or a quadratic remainder is modulo .
The theorem follows from the fact that a power of is a quadratic remainder modulo if and only if the exponent is even.
An attacker can therefore check whether the criterion from this theorem is met. He cannot always decide whether there is a Diffie-Hellman triple, but his answer is 75% correct. Its advantage over pure guessing is 50%.
Choice of public numbers
DEM prime p
The security of the procedure is based not least on the length of the numbers chosen. The prime number has to be chosen in such a way that discrete logarithms modulo cannot be calculated (efficiently enough) with currently known methods. The larger the prime number used, the safer the process, but also the more complex. The Federal Office for Information Security recommends a key length of at least 3000 bits (as of 2017).
The DEM prime number must also be chosen in such a way that algorithms for calculating the discrete logarithm are not easy. For example, it must be avoided that only has small prime factors. Otherwise the Pohlig-Hellman algorithm can be used, which does not depend on the group order but on the largest factor of the group order. In addition, it should be as unsuitable as possible for the number body sieve . This is the case when there is an irreducible polynomial of degree 5 that has very small coefficients and a zero .
"Generator" g
The number should be chosen so that all numbers between and as a result of the modular power come into question. Only then is it too time-consuming to try out all the numbers (if the prime number has also been chosen large enough). The number satisfies this property if it is a primitive root to the module , i.e. H. a producer of the group . For example , if Alice and Bob choose, the method still works, but the key is in any case , because is exactly the generator of the subgroup of with one element. The procedure is similarly unsafe if Alice and Bob choose a different small subgroup for a generator. The method is safer with a generator from a large subgroup, but it is best to choose a generator from the entire group. Since half of all the numbers are smaller such generators, there is enough choice.
As shown in the section “Prime residue class group and primitive root”, a primitive root can be found relatively easily if one chooses the DEM prime as having a prime number . However, as shown in the previous section, the Decisional Diffie-Hellman problem can be attacked by choosing as the primitive root.
"If one chooses instead so that the remainder class of modulo has a prime number order with a sufficiently large prime number , then according to today's view, DDH is considered difficult."
Use of fixed groups and prime numbers
Since generating secure primes is computationally expensive, many implementations use a fixed prime number . Some network protocols such as Internet Key Exchange provide a list of possible groups and their prime numbers.
The use of fixed groups and prime numbers can be exploited by an attacker to pre-execute much of the computation to break the discrete logarithm and to attack multiple targets simultaneously. The number field sieve algorithm consists of four steps, whereby the first three steps only require the prime number . If this is known, an attacker can pre-calculate the majority and reuse the results for every key exchange based on this. As a result, for example, the Logjam attack in TLS can break a 512-bit DEM key exchange in around 70 seconds after a one-week precalculation.
A team of researchers estimates that by pre-computing the 10 most common 1024-bit prime numbers, an attacker can decrypt the network traffic of 66% of VPNs , 26% of SSH servers, 16% of SMTP servers, and 24% of HTTPS websites on the Internet. The researchers estimate that the computational effort needed to break 1024-bit Diffie-Hellman could be done by a government attacker like the National Security Agency .
Man-in-the-middle attack
The Diffie-Hellman-Merkle key exchange is no longer secure if the attacker can change data packets in a man-in-the-middle attack . In the Alice and Bob model, such an attacker who can actively intervene in the action is called Mallory (from English malicious , dt. I.e. Sneaky , insidious). In a man-in-the-middle attack, Mallory intercepts the messages sent by Alice and Bob and sends his own message instead
further, he of any number and the publicly known figures and calculated.
After the key exchange, the two communication partners Alice and Bob have different keys and . In principle, a DHM key exchange was carried out twice: once between Alice and the attacker Mallory and once between Mallory and Bob. Mallory learns the two keys and .
Since Alice and Bob assume that they are communicating with each other, Mallory can eavesdrop on the following symmetrically encrypted communication. He will continue to redirect this via himself. Mallory also decrypts Alice's data and encrypts them again before he forwards them to Bob. Mallory can read the message content as well as change it unnoticed. He uses the same procedure for the opposite direction.
In order to rule out such a man-in-the-middle attack, the exchanged messages must be authenticated . This requires an information advantage that can be achieved via an authenticated channel.
Side channel attacks
A side channel attack is a cryptanalysis method that uses the physical implementation of a cryptosystem in a device (e.g. a chip card , a security token or a hardware security module ) or in software . It is not the cryptographic process itself that is attacked, only a specific implementation. The principle is based on observing a cryptographic device during the execution of the cryptological algorithms and finding correlations between the observed data and the key used.
Time attack
In 1995, Paul Kocher published a novel method that enabled him to break implementations of Diffie-Hellman, RSA, and DSA: the timing attack .
The goal of the time attack is the discrete exponential function. If a crypto implementation calculates and calculates for any larger numbers , then this is almost always done with the square-and-multiply algorithm. In this case, an action is set for each bit : If the bit just processed has the value , then this action is a multiplication, otherwise a squaring. Since the computing times for the multiplications take longer than for the squarings, Eve can draw conclusions about the number of ones in from time measurements . If he varies the number , at some point the information will be sufficient to calculate. Corresponding implementations with 1024-bit keys can already be broken with a few thousand time measurements.
In order to prevent such time attacks, however, only delays have to be built into the encryption and decryption process during implementation. With the method known as blinding, for example, a random number is included at one point in the method, which is then removed again at another point. Another possibility is to design the process so that it always takes the same length of time, regardless of the input value.
Power attack

In 1998, Paul Kocher, Joshua Jaffe and Benjamin Jun first introduced the concept of electricity attack. In the event of a power attack, not only is the processing time measured, but also the power consumption with an oscilloscope . Smart cards are particularly susceptible to power attacks, as they rely on an external power supply. An attacker measures the encryption and decryption processes and tries to assign certain points on the power consumption curve to individual components of the process. Here, too, the square-and-multiply algorithm is a suitable goal, since it is often easy to distinguish between multiplications and squarings in terms of power consumption. Power attacks are a little more complex to perform than time attacks, but are considered more effective.
As a countermeasure against power attacks, the manufacturer of crypto modules can disguise power consumption by incorporating dummy operations into an encryption or decryption process. Another possibility is to create an artificial power noise that superimposes the actual power consumption.
Elliptic Curve Diffie-Hellman (ECDH)
Cryptosystems based on elliptic curves (ECC method for short, from English Elliptic Curve Cryptography ) are not independent cryptographic methods, but known DL methods that are implemented in a special way. Every method that is based on the discrete logarithm in finite fields can be easily transferred to elliptic curves and thus transformed into an elliptic curve cryptosystem. The operations used in the original method (multiplication and exponentiation) on the finite body are replaced by point addition and scalar multiplication on elliptic curves. The -fold addition of a point to itself (i.e. the multiplication with the scalar ) is denoted by and corresponds to an exponentiation in the original method. The principle was proposed by Victor S. Miller and Neal Koblitz independently of one another in the mid-1980s .
body
A body is a set with two inner two-digit links “ ” and “ ”, which are usually called “addition” and “multiplication”. A field is an Abelian group with regard to addition and multiplication without zero and the distributive laws apply . The best known field is the set of real numbers on which addition and multiplication are defined in the usual way.
For a prime number , the set of numbers between and with both modulo addition and modulo multiplication without zero forms a group. The remainder classes of integers modulo , written or , thus form a finite field (also Galois field , English Galois field ). In addition, there is exactly one field with elements for every prime number and every natural number (except for isomorphism ) , which is denoted by or . In the elliptic curve cryptography are in particular the two special cases and important, so and . These are the best way to implement ECC processes.
Elliptic curves
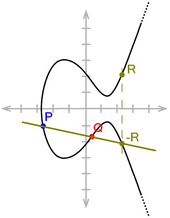
An elliptic curve (EC) is a set of points with values from a body that satisfy a cubic equation of the following form:
The (real) coefficients and must meet the condition to exclude singularities.
An elliptic curve is a smooth 3-order algebraic curve in the projective plane . Elliptic curves are mostly shown as curves in the affine plane , but they have an additional point at infinity, which is referred to here as (read "O"), but should not be confused with the zero point of the coordinate system . Above the body of the real numbers, the points form a curve in the real plane.
An important property of elliptical curves is the following: If a straight line intersects such a curve, there are exactly three points of intersection. The following cases occur:
- In a straight line that runs parallel to the axis, there is one of the three intersection points .
- In the case of a straight line that touches the curve, the contact point is counted as a double intersection.
- The intersection points are obvious for all other straight lines.
This property allows a group to be defined with the help of elliptical curves :
Let be the set of points of an elliptic curve united with the point at infinity. The group operation, commonly called point addition, is defined as follows:
- To calculate the sum of two points and , draw a straight line through and (if so , draw the tangent to EC )
- Find the third point of intersection of this straight line with the curve EC. (If the straight line runs parallel to the -axis, this is the intersection .)
- The sum is the point of EC, which is created by mirroring at the -axis. The reflection of is again .
The neutral element of the group is . It applies to all points on the elliptic curve. The inverse of a point is obtained by applying a straight line to it that runs parallel to the axis. If this straight line is a tangent, then the point itself is its inverse element.
The point is designated with , correspondingly one defines as -fold addition of the point . If the point is not , any point on curve E can be reached in this way (i.e., for every point on the curve there is a natural number with ) if one knows the correct generators of the group. (See also section Group operation in the article "Elliptic curve")
The task of determining this value from given points is called the discrete logarithm problem of elliptic curves ( ECDLP for short ). It is believed that the ECDLP (with proper curve choice) is heavy; H. cannot be resolved efficiently. This means that elliptical curves are ideal for implementing asymmetrical cryptosystems on them.
The construction for is very clear , since the points can be expressed in the real plane. However, this construction can be transferred to any body. In cryptography, elliptic curves are of shape and importance.
Example:
Let be the elliptic curve
given over the body .
So it is and and it applies . The set of all with and is thus together with an elliptic curve over .
This results in the following points:
| Points | |||
|---|---|---|---|
| and | , | ||
| - | - | ||
| and | , | ||
| and | , | ||
| and | , | ||
| - |
Diffie-Hellman based on elliptic curves
In cryptosystems based on elliptic curves, arithmetic operations in or are used instead of arithmetic operations . Again, efficient algorithms exist in these fields for calculating the power function, but not for calculating the logarithm.
Instead of a modulus, Alice and Bob now have to agree on a certain elliptic curve, i. H. on a body (or ) and a group (or ) based on it. All parameters in the exponent are (as before) natural numbers, while the base of a power is an element of .
An exponentiation over is more complex than an exponentiation over because it is composed of several arithmetic operations in . On the other hand, the calculation of the logarithm is also much "more difficult". The main advantage of using is therefore that Alice and Bob can use a group of smaller cardinality with the same security. This results in shorter key lengths, shorter signatures and shorter computing times.
The complexity of the logarithm increases with linear, in contrast "only" logarithmically. A key length of 1,024 bits based on the discrete logarithm can be shortened to 200 bits by using elliptical curves, for example, without any loss of security. The saving in computing time is usually given by a factor of 10.
Ephemeral Diffie-Hellman
In the context of the encryption protocol Transport Layer Security (TLS), Ephemeral Diffie-Hellman ( English ephemeral : short-lived, volatile) describes the use of Diffie-Hellman with new parameters for each new TLS session. With static Diffie-Hellman, the same parameters that are derived from a public-key certificate are reused for each TLS session . The same algorithm is used in both cases and only the parameters differ.
The use of ephemeral Diffie-Hellman to negotiate a symmetric session key offers forward secrecy , in contrast to the encrypted transmission of a session key with a public-key encryption method , for example RSA .
literature
General overview
- Albrecht Beutelspacher : Secret Languages. History and techniques. 3rd, updated edition, CH Beck: Munich, 2002.
- Albrecht Beutelspacher, Jörg Schwenk, Klaus-Dieter Wolfenstetter: Modern methods of cryptography. From RSA to zero knowledge. 8th edition, Springer Spectrum: Berlin, Heidelberg, 2015.
- Thomas Borys: Coding and Cryptology. Facets of application-oriented mathematics in the educational process. Vieweg + Teubner: Wiesbaden, 2011.
- Johannes Buchmann : Introduction to Cryptography. 6th edition, Springer Spectrum: Berlin, Heidelberg, 2016.
- Karin Freiermuth, Juraj Hromkovič , Lucia Keller, Björn Steffen: Introduction to cryptology. Textbook for teaching and self-study. 2nd edition, Springer Vieweg: Wiesbaden, 2014.
- Klaus Schmeh : Cryptography. Procedures, protocols, infrastructures. 5th updated edition, dpunkt.verlag: Heidelberg, 2013.
- Simon Singh : Secret Messages . The art of encryption from ancient times to the Internet. 13th edition, dtv Verlagsgesellschaft: München, 2016 (English original edition: The Code Book. The Science of Secrecy from Ancient Egypt to Quantum Cryptography. Fourth Estate: London, 1999).
Technical article
- David Adrian, Karthikeyan Bhargavan, Zakir Durumeric, Pierrick Gaudry, Matthew Green, J. Alex Halderman, Nadia Heninger, Drew Springall, Emmanuel Thomé, Luke Valenta, Benjamin VanderSloot, Eric Wustrow, Santiago Zanella-Béguelin, Paul Zimmermann: Imperfect Forward Secrecy: How Diffie-Hellman Fails in Practice. In: Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security. ACM, New York 2015, pp. 5-17. ( Online )
- Dan Boneh : The Decision Diffie – Hellman Problem. In: Proceedings of the Third Algorithmic Number Theory Symposium (Lecture Notes in Computer Science, Vol. 1423) Springer-Verlag, 1998, pp. 48-63. ( Online )
- Whitfield Diffie , Martin E. Hellman : New Directions in Cryptography. In: IEEE Transactions on Information Theory 22, No. 6, 1976, pp. 644-654. ( Online )
- Martin E. Hellman: An overview of public key cryptography. In: IEEE Communications Magazine 40, No. 5, 2002, pp. 42-49 ( online ). Original article : An overview of public key cryptography. In: IEEE Communications Magazine 16, No. 6, 1978, pp. 24-32 ( online )
- Paul C. Kocher : Cryptanalysis of Diffie-Hellman, RSA, DSS, and Other Systems Using Timing Attacks. In: Advances in Cryptology, CRYPTO '95 (15th Annual International Cryptology Conference), Springer-Verlag, 1995, pp. 27-31. ( Online )
- Paul C. Kocher: Timing Attacks on Implementations of Diffie-Hellman, RSA, DSS, and Other Systems. In: Advances in Cryptology, CRYPTO '96 (Lecture Notes in Computer Science, Vol. 1109), Springer-Verlag, 1996, pp. 104-113. ( Online )
- Paul Kocher, Joshua Jaffe, Benjamin Jun: Introduction to Differential Power Analysis and Related Attacks. In: Advances in Cryptology — CRYPTO '99, 19th Annual International Cryptology Conference. (Lecture Notes in Computer Science, Vol. 1666) Springer-Verlag: Berlin, 1999, pp. 388-397. ( Online )
- Ueli Maurer : Towards the equivalence of breaking the Diffie-Hellman protocol and computing discrete logarithms. In: Advances in Cryptology - Crypto '94. Springer-Verlag, 1994, pp. 271-281, doi: 10.1007 / 3-540-48658-5_26 .
- Ralph C. Merkle : Secure Communications over Insecure Channels . In: Communications of the ACM 21, No. 4, April 1978, pp. 294-299. ( Online )
application
- Anatol Badach, Erwin Hoffmann: Technology of the IP networks. Internet communication in theory and use. 3rd, revised and expanded edition, Hanser: München, 2015.
- Wolfgang Ertel : Applied cryptography. 4th edition, Hanser: Munich, 2012.
- Patrick Horster (Ed.): Chip cards. Basics, implementation, security aspects, applications. vieweg, 1998.
- Michael Welschenbach: Cryptography in C and C ++. Fundamentals of number theory, computer arithmetic with large numbers, cryptographic tools. 2nd, revised and expanded edition, Springer: Berlin, Heidelberg, 2012.
Mathematical basics
- Eric Bach, Jeffrey Shallit : Algorithmic Number Theory. Volume 1: Efficient Algorithms. MIT Press: Cambridge (MA), London, 1996.
- Christian Karpfinger, Kurt Meyberg: Algebra. Groups, rings, bodies. 3rd edition, Springer Spectrum: Berlin, Heidelberg, 2013.
- Ramanujachary Kumanduri, Cristina Romero: Number Theory with Computer Applications. Pearson: Prentice Hall, 1998.
- Paulo Ribenboim : The world of prime numbers. Secrets and Records. 2nd, completely revised and updated edition, Springer: Berlin, Heidelberg, 2011.
- Lawrence C. Washington : Elliptic Curves. Number Theory and Cryptography. Second Edition, Chapman & Hall / CRC Press: Boca Raton (FL), 2005, pp. 95-97.
Web links
- Federal Office for Information Security (BSI): BSI - Technical Guidelines: Cryptographic Procedures: Recommendations and Key Lengths Version 2016-01, as of February 15, 2016.
- ECRYPT II: European Network of Excellence in Cryptology II
- Steven Levy: The Open Secret - Public key cryptography - the breakthrough that revolutionized email and ecommerce - was first discovered by American geeks. Right? Wrong. In: WIRED (published: January 4, 1999; accessed: May 9, 2016)
Individual evidence
- ↑ So u. a. Yiu Shing Terry Tin et al. a .: Provably Secure Mobile Key Exchange: Applying the Canetti-Krawczyk Approach. In: Rei Safavi-Naini, Jennifer Seberry: Information Security and Privacy. 8th Australasian Conference, ACISP 2003, Springer: Berlin, Heidelberg, 2003, pp. 166–179.
- ↑ Ralph Merkle: Secure Communications over Insecure Channels. In: Communications of the ACM 21, No. 4, April 1978, pp. 294-299.
- ^ Whitfield Diffie, Martin Hellman: New Directions in Cryptography. In: IEEE Transactions on Information Theory. 22, No. 6, 1976, pp. 644-654.
- ^ Schmeh: Cryptography. 5th edition, 2013, p. 185.
- ^ Martin E. Hellman: An overview of public key cryptography. In: IEEE Communications Magazine 40 (5), 2002, pp. 42-49.
- ↑ Badach, Hoffmann: Technology of IP networks. 3rd edition, 2015, p. 53.
- ↑ a b Freiermuth u. a .: Introduction to cryptology. 2nd edition, 2014, p. 200.
- ↑ a b Schmeh: Cryptography. 5th edition, 2013, p. 187.
- ^ Taher Elgamal: A public key cryptosystem and a signature scheme based on discrete logarithms. In: IEEE Transactions on Information Theory 31, 1985, pp. 469-472. See also HW Lang: Cryptographic Protocols: ElGamal Encryption (created: February 19, 2010, updated: May 29, 2015).
- ^ Beutelspacher: Secret languages. 3rd ed., 2002, p. 54.
- ^ Schmeh: Cryptography. 5th ed., 2013, pp. 204-209.
- ^ Beutelspacher: Secret languages. 3rd ed., 2002, p. 53.
- ^ Welschenbach: Cryptography in C and C ++. 2nd edition, 2012.
- ↑ Cryptographic apparatus and method, US 4200770 A and Public key cryptographic apparatus and method, US 4218582 A
- ^ Association for Computing Machinery: Cryptography Pioneers Receive ACM AM Turing Award (accessed May 1, 2016).
- ↑ Borys: Coding and Cryptology. 2011, pp. 155–156.
- ^ Schmeh: Cryptography. 5th ed., 2013, pp. 39–42.
- ↑ a b Ertel: Applied cryptography. 4th ed., 2012, p. 77; Buchmann: Introduction to Cryptography. 3rd edition, 2004, p. 153.
- ^ Schmeh: Cryptography. 5th ed., 2013, p. 176.
- ^ Ertel: Applied cryptography. 4th ed., 2012, pp. 98-99; Buchmann: Introduction to Cryptography. 3rd edition, 2004, p. 192.
- ↑ Beutelspacher, Schwenk, Wolfenstetter: Modern methods of cryptography. 8th edition, 2015, p. 16.
- ↑ Beutelspacher, Schwenk, Wolfenstetter: Modern methods of cryptography. 8th edition, 2015, p. 17 with reference to Jose L. Balcazar, Josep Diaz, Josep, Joaquim Gabarró: Structural Complexity I. Springer: Heidelberg, Berlin, 1988.
- ↑ a b Schmeh: Cryptography. 5th edition, 2013, p. 184.
- ^ Schmeh: Cryptography. 5th ed., 2013, pp. 181-183.
- ↑ a b Freiermuth u. a .: Introduction to cryptology. 2nd edition, 2014, p. 202.
- ^ Schmeh: Cryptography. 5th edition, 2013, p. 183.
- ↑ Freiermuth u. a .: Introduction to cryptology. 2nd ed., 2014, pp. 202–203.
- ↑ Buchmann: Introduction to Cryptography. 6th ed., 2016, pp. 67–68.
- ↑ a b Schmeh: Cryptography. 5th ed., 2013, pp. 185–186.
- ↑ Freiermuth u. a .: Introduction to cryptology. 2nd edition, 2014, p. 199.
- ↑ Freiermuth u. a .: Introduction to cryptology. 2nd ed., 2014, pp. 200–202.
- ↑ a b Buchmann: Introduction to Cryptography. 6th edition, 2016, p. 190.
- ^ Ueli Maurer : Towards the equivalence of breaking the Diffie-Hellman protocol and computing discrete logarithms. In: Advances in Cryptology - Crypto '94. Springer-Verlag, 1994, pp. 271-281.
- ↑ Buchmann: Introduction to Cryptography. 6th ed., 2016, p. 190. See also: Dan Boneh: The Decision Diffie – Hellman Problem. In: Proceedings of the Third Algorithmic Number Theory Symposium (Lecture Notes in Computer Science, Vol. 1423) Springer-Verlag, 1998, pp. 48-63.
- ↑ For a proof see Buchmann: Introduction to Cryptography. 6th edition, 2016, pp. 191–192.
- ↑ Buchmann: Introduction to Cryptography. 6th ed., 2016, pp. 192–193.
- ↑ Federal Office for Information Security: BSI - Technical Guidelines: Cryptographic Procedures: Recommendations and Key Lengths Version 2016-01, as of February 15, 2016. For calculated minimum sizes of p, see also ECRYPT II: European Network of Excellence in Cryptology II .
- ↑ a b Buchmann: Introduction to Cryptography. 6th edition, 2016, p. 193.
- ↑ a b c Adrian u. a .: Imperfect Forward Secrecy: How Diffie-Hellman Fails in Practice. In: Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security. 2015, pp. 5–15.
- ↑ Shafi Goldwasser , Mihir Bellare : Lecture Notes on Cryptography. 2008, section 11.1.5 and 11.2.
- ^ Paul C. Kocher: Cryptanalysis of Diffie-Hellman, RSA, DSS, and Other Systems Using Timing Attacks. In: Advances in Cryptology, Crypto '95 (15th Annual International Cryptology Conference), Springer-Verlag, 1995, pp. 27-31. ( Online )
- ^ Schmeh: Cryptography. 5th ed., 2013, pp. 320–321.
- ^ Schmeh: Cryptography. 5th edition, 2013, p. 321.
- ^ Paul Kocher, Joshua Jaffe, Benjamin Jun: Introduction to Differential Power Analysis and Related Attacks. In: Advances in Cryptology — CRYPTO '99, 19th Annual International Cryptology Conference. (Lecture Notes in Computer Science, Vol. 1666) Springer-Verlang: Berlin, 1999, pp. 388-397.
- ^ Schmeh: Cryptography. 5th ed., 2013, pp. 321–322.
- ^ Schmeh: Cryptography. 5th ed., 2013, pp. 323-324.
- ^ Victor S. Miller: Use of Elliptic Curves in Cryptography. In: Advances in Cryptology - CRYPTO '85 Proceedings (= Lecture Notes in Computer Science. 218). Springer, 1986, pp. 417-426
- ^ Neal Koblitz: Elliptic Curve Cryptosystems. In: Mathematics of Computation 48, No. 177, American Mathematical Society, 1987, pp. 203-209.
- ^ Schmeh: Cryptography. 5th edition, 2013, p. 212.
- ↑ a b c Beutelspacher, Schwenk, Wolfenstetter: Modern methods of cryptography. 8th edition, 2015, p. 148.
- ↑ a b Schmeh: Cryptography. 5th ed., 2013, pp. 214–215.
- ↑ Washington: Elliptic Curves. 2nd ed., 2008, pp. 95-97.
- ↑ a b c Schmeh: Cryptography. 5th ed., 2013, p. 215.


























![{\ displaystyle [0.6]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b0c99f608fe4838dc2e6fd517321a0344a2ad44)































































































































































































