Caesar encryption
The Caesar encryption (also known as Caesar cipher , Caesar algorithm , Caesar shift , shift cipher or simple Caesar ) is a simple symmetrical encryption method based on monographic and monoalphabetic substitution . As one of the simplest and most insecure methods today, it is mainly used to clearly illustrate the basic principles of cryptology . For the sake of simplicity, only the 26 letters of the Latin alphabet are often used as the alphabet for plain text and ciphertext without a distinction between uppercase and lowercase letters , and special characters, punctuation marks, etc. are ignored.
algorithm
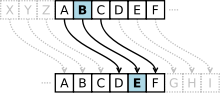
With encryption , each letter of the plaintext is mapped to a ciphertext letter . This figure is obtained by shifting the characters of an ordered alphabet cyclically to the right by a certain number (rotating); cyclical means that when you move beyond Z, you start counting again at A. The number of characters shifted forms the key , which remains unchanged for the entire encryption process. Example of a shift by three characters:
Klar: a b c d e f g h i j k l m n o p q r s t u v w x y z Geheim: D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
The plain text “caesar” becomes the ciphertext “FDHVDU”. For decryption, the alphabet is rotated to the left by the same number of characters.
Mathematically, the Caesar encryption can be described with the help of the modulo addition. To do this, all characters of the alphabet are first mapped onto a remainder class ring , for example a = 0, b = 1, c = 2,…, z = 25. The encryption of a plaintext letter with a shift of characters and an alphabet with 26 characters is then defined as:
Correspondingly, the decryption of a ciphertext letter is :
history
The name of the Caesar encryption is derived from the Roman general Gaius Julius Caesar , who, according to the tradition of the Roman writer Suetonius, used this type of secret communication for his military correspondence. Caesar used a shift in the alphabet by three letters.
Suetonius describes the procedure as follows:
"[...] si qua occultius perferenda erant, per notas scripsit, id est sic structo litterarum ordine, ut nullum verbum effici posset: quae si quis investigare et persequi velit, quartam elementorum litteram, id est D pro A et perinde reliquas commutet."
"[...] when something secret was to be conveyed, he wrote in characters, that is, he arranged the letters so that no word could be read: To read them, you swap the fourth letter, D for A and the same with the rest. "
After Suetonius, the Roman emperor Augustus also used the method, but with a shift by one letter and without a rotation of the alphabet. Instead of an X , the last letter of the Latin alphabet at the time , Augustus wrote AA .
Leon Battista Alberti improved the method in the 15th century with the development of the cipher disk . The cipher disk makes it easier to carry out the Caesar encryption with any shifts, as the inner disk is rotated by the number of shifted letters relative to the outer disk and the replaced letters can thus be read off. In addition, Alberti also described the use of the cipher disk or its variants for carrying out more complex monoalphabetic and polyalphabetic substitution processes .
In 1508 Trithemius described a polyalphabetic substitution process with the help of the tabula recta he had invented . This method, which became known as Vigenère encryption in the 16th century , is essentially based on Caesar encryption, but with a different shift for each letter, which significantly increases security.
Decipherment and Security
Like all monoalphabetic encryption methods, the shift cipher does not offer sufficient security against unauthorized decipherment and can be " cracked " very easily . The uneven distribution of letters in natural language is not hidden by this type of encryption, so that a frequency analysis reveals the effect of a simple monoalphabetic substitution.
The following diagram shows the frequency distribution of the letters in a longer text in German:

As you would expect, the most common letter is E, followed by N and I, as is usually the case in German. If the text is encrypted with the key 10 (or in other words, with the key letter J), a ciphertext is obtained with the following frequency distribution:

The most common letter here is O, followed by X and S. You can see at first glance that the German “frequency range” has been shifted ten digits back and thus has the key. The only requirement is that one can predict the distribution of the characters in the original text.
If you do not have this information or if you want to do without the frequency analysis, you can also take advantage of the fact that only a very small number of possible keys are possible with the Caesar cipher. Since the size of the key space is only 25, which corresponds to a " key length " of not even 5 bits , the plain text is available after the 25th attempt at the latest after trying it out. An exhaustive key search ( exhaustion ) can be implemented trivially with Caesar encryption. Since this is also possible without a computer or calculating machine with little effort, the security of Caesar encryption was not based on the secrecy of the key, but essentially on the secrecy of the procedure, and thus does not correspond to that postulated in the 19th century Principle of Auguste Kerckhoffs .
Key letter
The shift of the alphabet by N characters (N = 1… 25) represents the key. Instead of specifying the shift as a number, it can also be specified as a key letter. There are two common conventions here :
- A corresponds to no shift, B to a shift of 1, C to a shift of 2, etc.
- A corresponds to a shift of 1, B to a shift of 2, C to a shift of 3, etc.
The first convention arises when reading the key letter from the two alphabets lying one above the other (“a” to “D” is a shift of three characters). This is also common with the related Vigenère encryption . In addition, this convention corresponds to the mapping from letter to number, as it is usually carried out for the modulo calculation. The second convention corresponds to the natural numbering of the displacements. There is no historical reference to the fact that Caesar and Augustus used their first letter as a key letter from Suetonius.
Since both conventions contradict each other, specifying a key letter is ambiguous, while specifying a number is unambiguous.
variants
Today, the Caesar cipher is as ROT13 with a shift to 13 characters in use to text content such as spoilers or punch lines to read against inadvertent disguise . Since today's Latin alphabet consists of 26 characters, the cyclical shift of 13 characters first encrypts the text and a second encryption with the same key achieves a total shift of 26 characters, thus recovering the original text. This is a particularly simple case of involutive encryption. In involutive methods, encryption and decryption are identical, and a double application of the method returns the original plain text.
In addition to the use of a modified alphabet, which includes digits and special characters , there is also the variant of the reverse or reverse Caesar encryption . The sequence of the secret alphabet is reversed and a shift is carried out. A shift of four characters then results in the following alphabet:
Klar: a b c d e f g h i j k l m n o p q r s t u v w x y z Geheim: D C B A Z Y X W V U T S R Q P O N M L K J I H G F E
In this case, “caesar” would become the ciphertext “BDZLDM”. Another variant is created if you omit the shift in the reverted Caesar encryption and thus result in the following alphabet:
Klar: a b c d e f g h i j k l m n o p q r s t u v w x y z Geheim: Z Y X W V U T S R Q P O N M L K J I H G F E D C B A
This variant is known as Atbash using the Hebrew alphabet .
literature
- Friedrich L. Bauer : Deciphered Secrets. Methods and maxims of cryptology. 3rd, revised and expanded edition. Springer, Berlin a. a. 2000, ISBN 3-540-67931-6 .
- Rudolf Kippenhahn : Encrypted messages. The secret script of Julius Caesar - Secret scripts in World War I and II - The Pope's code book - Enigma. 4th edition. Nikol, Hamburg 2006, ISBN 3-937872-37-X .
Web links
- Tool for trying out the Caesar codes
- Tool for encryption with Caesar cipher, affine cipher and ROT13
- Tool for brute force attacks on Caesar ciphers or to "break" them
- Online encryption website (ROT1 to ROT25)
- Video: Caesar Encryption . Christian Spannagel 2012, made available by the Technical Information Library (TIB), doi : 10.5446 / 19812 .
- A version of the Caesar algorithm written in C.