Downhill simplex method

In contrast to the namesake for linear problems ( simplex algorithm ), the downhill simplex method or Nelder-Mead method is a method for optimizing non-linear functions of several parameters . It falls into the category of hill climbing or downhill search methods . It can be used e.g. B. also when fitting curves .

It was introduced by John Nelder and Roger Mead in 1965.

Basics

Example run with Rosenbrock "banana function"

Example run with sky blue function

A special feature of this simplex algorithm is that the function does not need to be derived from the parameters, which for some problems cannot be calculated with reasonable effort. By meaningful comparisons of the function values ​​of several points in the parameter space, the tendency of the values ​​and the gradient towards the optimum are approximated , similar to a Regula falsi with step size control . The method does not converge extremely quickly, but it is simple and relatively robust.

The algorithm is based on a simplex , the simplest volume in the -dimensional parameter space, which is spanned from points. In the one-dimensional on the number line this is a line , in the two-dimensional a triangle , etc. Each point corresponds to a (coordinate) set of parameters (or variables), and a function value can be calculated for each point. B. can be viewed as an error or cost value. The “worst” and the “best” are then determined from these points. From one iteration step to the next, the “worst” of these points is usually replaced by a new one that is hopefully “better”. The “best” point is always retained as the best solution so far. ${\displaystyle N}$ ${\displaystyle N+1}$ ${\displaystyle N+1}$

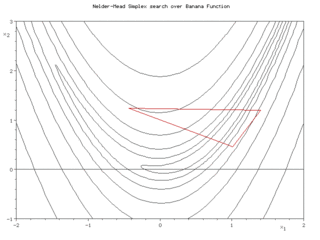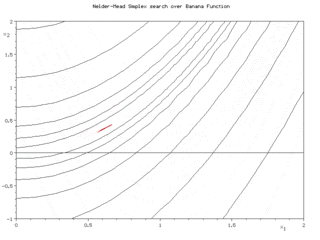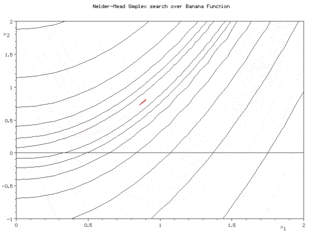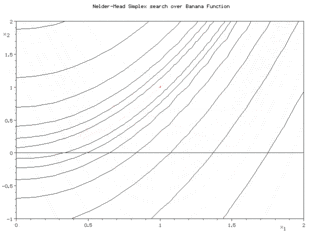
In a two-dimensional visualization with contour lines for the function to be optimized, one sees (in the pictures on the right) a triangle that purposefully approaches the optimum by folding around one of its sides, stretching or contracting around it near the optimum . See also the picture at the bottom.

Without derivations, various cases, such as the pathological behavior of these derivations in the event of discontinuities , do not apply , so that although the method generally converges more slowly (namely linearly) than optimization methods with derivations, it works much more robustly. The possible traps in the simplex method are, similar to most optimization methods, unexpected local secondary minima (or optima) that can be converged on, or that the method contracts too early to a constant value for one or more parameters.

algorithm

Flowchart of the downhill simplex method

The downhill simplex method finds a local optimum of a function with variables (parameters). An objective function is given that assigns a value (quality of the solution) to each point in the solution space. ${\displaystyle N}$ ${\displaystyle f:\mathbb {R} ^{N}\rightarrow \mathbb {R} }$

1. choose starting points that make up the simplex ${\displaystyle N+1}$ ${\displaystyle x_{0},x_{1},\cdots ,x_{N}\in \mathbb {R} ^{N}}$
2. sort the points by the value of the objective function so that is best, second worst, and worst ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle x_{N-1}}$ ${\displaystyle x_{N}}$
3. center all but the worst point: ${\displaystyle m={\frac {1}{N}}\sum \nolimits _{i=0}^{N-1}x_{i}}$
4. reflect the worst point at the center: ${\displaystyle r=(1+\alpha )m-\alpha x_{N}}$
5. if is better than : find the expanded point , replace with the better of the two points and go to step 2 ${\displaystyle r}$ ${\displaystyle x_{0}}$ ${\displaystyle e=(1+\gamma )m-\gamma x_{N}}$ ${\displaystyle x_{N}}$ ${\displaystyle e,r}$
6. if is better than the second worst point : replace with and go to step 2 ${\displaystyle r}$ ${\displaystyle x_{N-1}}$ ${\displaystyle x_{N}}$ ${\displaystyle r}$
7. be the better of the two points . Find the contracted point ${\displaystyle h}$ ${\displaystyle x_{N},r}$ ${\displaystyle c=\beta m+(1-\beta )h}$
8. if is better than : replace with and go to step 2 ${\displaystyle c}$ ${\displaystyle x_{N}}$ ${\displaystyle x_{N}}$ ${\displaystyle c}$
9. compress the simplex: for each : replace with ${\displaystyle i\in \{1,\cdots ,N\}}$ ${\displaystyle x_{i}}$ ${\displaystyle \sigma x_{0}+(1-\sigma )x_{i}}$
10. go to step 2

According to these rules, the iteration is continued until a convergence criterion is met. The simplex will shift in the direction of a local optimum and finally contract around this.

${\displaystyle \alpha ,\beta ,\gamma }$and are parameters of the algorithm. Typical parameter values ​​are: ${\displaystyle \sigma }$

• ${\displaystyle \alpha =1}$ (Reflection)
• ${\displaystyle \gamma =2}$ (Expansion)
• ${\displaystyle \beta =1/2}$ (Contraction)
• ${\displaystyle \sigma =1/2}$ (Compression)

It must and be. ${\displaystyle 0<\alpha <\gamma }$ ${\displaystyle \beta ,\sigma \in ]0,1[}$

The starting points must be chosen so that they span a simplex of the dimension and not all lie in a hyperplane of smaller dimension, i.e. H. the vectors must be linearly independent . You can z. B. select a point as the starting point and determine others by increasing one of the parameters by a factor different from 1 (if the parameter cannot be 0) or a summand different from 0. Alternatively: Two different values ​​are given for each parameter, the first point is calculated with all initial values ​​and the other points also with the initial values, only that one of the parameters is replaced by its second value. Or you choose random points from the solution space. ${\displaystyle N+1}$ ${\displaystyle N}$ ${\displaystyle x_{1}-x_{0},x_{2}-x_{0},...,x_{N}-x_{0}}$ ${\displaystyle N}$ ${\displaystyle N}$

Extensions for emergencies

As with other methods, there is always the risk of converging on a secondary optimum. There are several measures that can be taken to reduce this risk:

• After a certain number of steps a new start is made. For this purpose, the previously best point is retained and a new start simplex is built around it, by adding the coordinate (only) of one parameter, e.g. B. is varied by 5%.
• Exactly as before, only the additional simplex points are made even more flexible by random values.
• Instead of taking such measures after a fixed number of steps, the point in time can also be made dependent on the current status of the iteration. To do this, the problem must of course be better known so that one can be sure of it.
• Alternatively, you can even make the time of the rescheduling variable using a random number.
• An additional security query could intercept the case that only one of the parameters got stuck prematurely, then you could send him special treatment.

All of these variants require intensive preoccupation with the respective specific problem, unfortunately there are no generally valid recipes for it.

Extension for curve fitting

If one does not want to optimize a single analytical function of parameters (coordinates), but rather adapt a theory function to a measurement curve, only a small additional step is necessary: ​​The function to be optimized is often the sum of squares, i.e. the sum of the squares of the differences from the individual measured values ​​(curve points) and the theory function values ​​at the same points, the latter depending on the one hand on the coordinate of the measurement curve and also on the parameters. It is irrelevant for the simplex method whether the square root is still extracted from the sum of squares. See also Least Squares Method . ${\displaystyle N}$ ${\displaystyle x}$ ${\displaystyle N}$

However, the downhill simplex method is very flexible (unlike the Levenberg-Marquardt algorithm , for example), so other optimization functions can also be used depending on the situation:

• The data have a strong scatter: Instead of the sum of the squared deviation, the sum of the amounts of the deviations is minimized . Outliers influence the result less.
• Curve fitting usually works with the assumption that the error of the dependent variable is independent of the associated independent variable ( homoscedasticity ). However, in some cases it is a function of . This situation occurs particularly when and extend over several orders of magnitude. If you were to minimize the sum of squares in such cases, you would get a good fit for large values, but a very bad fit for small ones, which hardly contribute to the sum of squares. In such cases , the sum of the squared relative deviations is minimized . ${\displaystyle (\Delta y=y_{calc}-y_{obs})}$ ${\displaystyle \Delta y}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x/y}$ ${\displaystyle \chi ^{2}}$ ${\displaystyle \Sigma (\Delta y/y)^{2}}$

Example implementation

Pseudocode ( C-like ):

// Deklarationen

// Benutzervorgaben, -eingaben
int NP= ... ;        // Anzahl der Parameter, die in FQS() eingehen,
                     // auch "Dimension des Parameterraums"

double ParP[NP]={ ... }; // primärer Parametersatz
double ParS[NP]={ ... }; // sekundärer Parametersatz, gibt Schwankungsbreite vor

double FQS(int pf)   // Zu minimierende Funktion, hängt
  {                  // von den Parametern Par0[pf][...] ab.
    ...              // Muss je nach Problemstellung erstellt werden.
                     // So schreiben, dass sie für den Parametersatz Nr. pf
  }                  // berechnet und am Schluss in Par0[pf][0] (s. u.)
                     // abgespeichert wird.

// Ende Benutzervorgaben

// Initialisierung

// Simplex-Parameter
double NA = 1, NB = .5, NC = 2; // Alpha, Beta, Gamma

// Parametersätze, NP+1 Stück für den Simplex selbst, plus 3 weitere
double Par0[NP+4][NP+1];
// darin 1. Index: 0..NP die (NP+1) Parametersätze des Simplex,
//                       dabei auf 0 immer der schlechteste Punkt des Simplex,
//                             auf 1 immer der beste Punkt des Simplex
//                 NP+1  Punkt P*, s. u.
//                 NP+2  Punkt P**, s. u.
//                 NP+3  Mittelpunkt P-Quer des Simplex, s. u.
// darin 2. Index: 0     Fehlerwert für diesen Satz
//                 1..NP einzelne Parameterwerte dieses Satzes

// Initialisierung

// Simplex aus Primär- und Sekundärwerten
Parametersätze 0 bis NP mit Primärwerten belegen;
In Parametersätzen 1 bis NP (i) jeweils
   Parameter Nr. i mit Sekundärwert belegen;

// Berechnung der Anfangs-Fehlersummen
für Parametersätze 0 bis NP: feh=FQS(i); // speichert Ergebnis in Par0[i][0], s. o.

// Schleife für Iteration, Hauptschleife
bool fertig = false;
while (!fertig)
    NT++; // Simplex-Schritt Nr. NT

    // schlechtesten und besten Punkt ermitteln (höchster bzw. niedrigster Fehlerwert)
    Werte fmin und fmax auf Fehlerwert von Satz Nr. 0 vorbelegen;
    für alle Parametersätze von 1 bis NP:
       wenn Fehler für Satz Nr. i größer als fmax:
          noch schlechterer Punkt, fmax auf diesen Wert, Punkt mit Nr. 0 tauschen
       wenn Fehler für Satz Nr. i kleiner als fmin:
          noch besserer Punkt, fmin auf diesen Wert, Punkt mit Nr. 1 tauschen

    // Konvergenzabfrage, sind wir fertig?
    // Dies muss auch je nach Problem individuell erstellt werden,
    // hier als Beispiel die Bedingung, dass alle Parameter nur noch um 1 ‰
    // schwanken.

    fertig = true;
    für alle Parameter in allen Parametersätzen von 0 bis NP:
       wenn nur für einen Parameter die relative Abweichung des Wertes
          zwischen schlechtestem und bestem Punkt größer als 0.001, dann:
             fertig=false; // doch noch nicht fertig

    //Wenn fertig, dann beende mit bestem Punkt Par0[1][1..3] als Ergebnis des Algorithmus

    // Mittelpunkt P-QUER des Simplex nach Index NP+3
    Mittelwerte über Sätze 1 bis NP (also ohne schlechtesten Punkt Nr. 0!) bilden
       und als Satz Nr. NP+3 speichern;

    // Punkt P* durch Reflexion des schlechtesten Punkts
    // am Mittelpunkt P-QUER (mit Nelder/Mead-Parameter alpha=NA) nach Index NP+1
    innerhalb eines Parametersatzes:
       Par0[NP+1][i]=(1 + NA) * Par0[NP+3][i] - NA * Par0[0][i];
    fs=Par0[NP+1][0]=FQS(NP+1); // und Fehler berechnen

    // Fallunterscheidung, ob Verbesserung erreicht
    wenn fs<fmin // neuer Punkt P* im Vergleich zu bisher bestem
    /  // ja, besser!
    |  // weiteren Schritt zu Punkt P** in dieselbe Richtung nach Index NP+2
    |  // (mit Nelder/Mead-Parameter gamma=NC)
    |  innerhalb eines Parametersatzes:
    |     Par0[NP+2][i]=(1 + NC) * Par0[NP+1][i] - NC * Par0[NP+3][i];
    |  fs=Par0[NP+2][0]=FQS(NP+2); // und Fehler berechnen
    |
    |  wenn fs>=fmin // wieder Vergleich mit bisher bestem Punkt
    |  /  // keine weitere Verbesserung: P** verwerfen, P* nach Index 0,
    |  |  // also bisher schlechtesten Wert durch neuen (etwas besseren) ersetzen
    |  \  Parametersatz Nr. NP+1 nach Nr. 0 kopieren;
    |  else // von fs>=fmin
    |  /  // ja, auch eine Verbesserung!
    |  |  // auch besser als P* ?
    |  |  wenn fs>Par0[NP+1][0]
    |  |  /  // nein, P* weiterverwenden und damit bisher schlechtesten auf Index 0 ersetzen
    |  |  \  Parametersatz Nr. NP+1 nach Nr. 0 kopieren;
    |  |  else // von fs>Par0[NP+1][0]
    |  |  /  // ja, P** weiterverwenden und damit bisher schlechtesten auf Index 0 ersetzen
    \  \  \  Parametersatz Nr. NP+2 nach Nr. 0 kopieren;

    else // von fs<fmin
    /  // nicht besser als bisher bester, nun prüfen, ob P* wenigstens überhaupt eine Verbesserung
    |  wenn fs von P* für wenigstens einen der Punkte 2..NP kleiner ist, dann:
    |  /  // ja, besser als mindestens einer, mit P* den bisher schlechtesten Punkt auf Index 0 ersetzen
    |  \  Parametersatz Nr. NP+1 nach Nr. 0 kopieren;
    |  else // von fs von P*
    |  /  // nein, weiterhin schlechter als die anderen Punkte
    |  |  // Zusatzprüfung: sogar schlechter als bisher schlechtester Punkt fmax?
    |  |  wenn fs>fmax // schlechter als bisher schlechtester?
    |  |     // ja, erstmal nichts tun
    |  |  else // von fs>fmax
    |  |  /  // nein, also wenigstens bisher schlechtesten Punkt damit ersetzen
    |  \  \  Parametersatz Nr. NP+1 nach Nr. 0 kopieren;
    |  // neuer Punkt P** durch Kontraktion zwischen bisher schlechtestem Punkt (Index 0)
    |  // und P-QUER (Index NP+3) nach Index NP+2 (mit Nelder/Mead-Parameter beta=NB)
    |  innerhalb eines Parametersatzes:
    |     Par0[NP+2][i]= NB * Par0[0][i] + (1 - NB) * Par0[NP+3][i];
    |  fs=Par0[NP+2][0]=FQS(NP+2); // und Fehler berechnen
    |  // P** besser als bisher schlechtester Punkt?
    |  wenn fs<fmax // besser als bisher schlechtester?
    |  /  // ja, bisher schlechtesten durch P** ersetzen
    |  \  Parametersatz Nr. NP+2 nach Nr. 0 kopieren;
    |  else // von fs<fmax
    |  /  // nein, keinerlei Verbesserung, Notfall
    |  |  // folgt allgemeine Kompression um Faktor 2 um den bisher besten Punkt herum
    |  |  für alle Parametersätze außer Nr. 1 (bisher bester): // also j=0 und 2..NP
    |  |     innerhalb eines Parametersatzes j:
    |  |        Par0[j][i]=(Par0[j][i] + Par0[1][i]) / 2;
    \  \     fs=Par0[j][0]=FQS(j); // und Fehler berechnen
    // Schleifenende

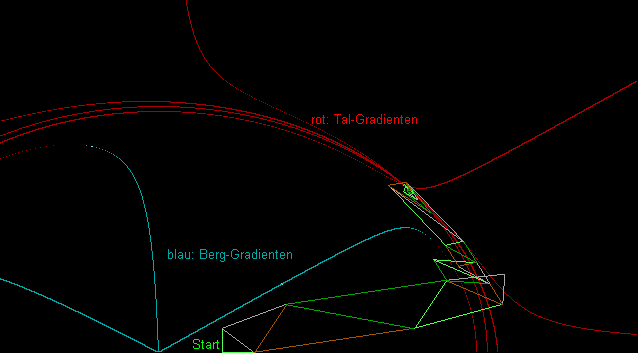
Graphic representation of an example run

The picture shows the result of a program run. The red and blue lines represent the gradient lines for valleys and mountains. It is a circular trench in an inclined plane, the local minimum within the circular trench is of interest here . The simplex iteration finds the minimum at the intersection of the red lines. The graphic ranges from 0 to 4 in - and - direction. ${\displaystyle x}$ ${\displaystyle y}$

literature

• John Ashworth Nelder, Roger Mead: A Simplex Method for Function Minimization . Computer Journal, 1965, 7, 308–313 ( original text as PDF file , 543 kB)
• William H. Press, Saul A. Teukolsky, William T. Vetter Ling, Brian P. Flannery: Numerical Recipes in C . Foundation Books 2007, ISBN 978-8185618166 .
• Jeffrey C. Lagarias, James A. Reeds, Margaret H. Wright, Paul E. Wright: Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions . In: SIAM Journal on Optimization . tape 9 , no. 1 , 1998, p. 112-147 , doi : 10.1137 / S1052623496303470 .
• Larry Nazareth, Paul Tseng: Gilding the Lily: A variant of the Nelder-Mead algorithm based on Golden-Section Search . Computational Optimization and Applications, Vol. 22 (2002), No. 1, pp. 133-144
• Saša Singer, Sanja Singer: Efficient implementation of the Nelder-Mead search algorithm. Applied Numerical Analysis and Computational Mathematics, Vol. 1 (2004), No. 2, pp. 524-534 (abstract)
• Marco A. Luersen, Rodolphe Le Riche: Globalized Nelder-Mead method for engineering optimization. Computers and Structures 82 (2004), pp. 2251-2260
• Andrej Prša, Tomaž Zwitter: Introducing adapted Nelder & Mead's downhill simplex method to a fully automated analysis of eclipsing binaries. In: C. Turon, KS O'Flaherty, MAC Perryman (Eds.): The Three-Dimensional Universe with Gaia (ESA SP-576). Proc. Gaia Sympos. 2004, ESA Publications Division, Nordwijk 2005, pp. 611–614
• David Byatt, Ian Coope, Chris Price: 40 years of the Nelder-Mead algorithm (PDF file; 3.46 MB)
• Fuchang Gao, Lixing Han: Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Computational Optimization and Applications 51 (2012), No. 1, pp. 259-277
• Jeffrey C. Lagarias, Bjorn Poonen, Margaret H. Wright: Convergence of the restricted Nelder-Mead algorithm in two dimensions. SIAM J. Optimization 22 (2012), No. 2, pp. 501-532

Individual evidence

1. ↑ Nelder, Mead A simplex method for function minimization , Computer Journal, Volume 7, 1965, pp. 308-313